Projective unitary group
Encyclopedia
In mathematics
, the projective unitary group PU(n) is the quotient
of the unitary group
U(n) by the right multiplication of its center, U(1), embedded as scalars.
Abstractly, it is the holomorphic isometry group
of complex projective space
, just as the projective orthogonal group
is the isometry group of real projective space
.
In terms of matrices
, elements of U(n) are complex n
n unitary matrices, and elements of the center are diagonal matrices equal to 
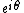multiplied by the identity matrix. Thus elements of PU(n) correspond to equivalence classes of unitary matrices under multiplication by a constant phase 
.
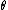Abstractly, given a Hermitian space V, the group PU(V) is the image of the unitary group U(V) in the automorphism group of the projective space
.
The projective special unitary group
PSU(n) is equal to the projective unitary group, in contrast to the orthogonal case.
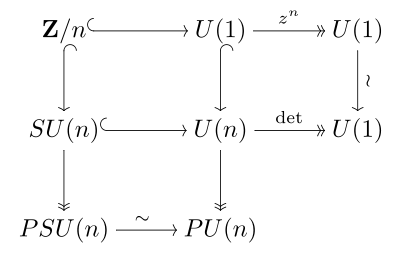
The connections between the U(n), SU(n), their centers, and the projective unitary groups is shown at right.
The center of the special unitary group
is the scalar matrices of the nth roots of unity:
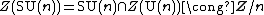
The natural map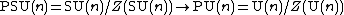
is an isomorphism, by the second isomorphism theorem, thus
and the special unitary group SU(n) is an n-fold cover of the projective unitary group.
.
At n = 2,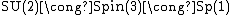
, all being representable by unit norm quaternions, and 
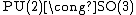, via: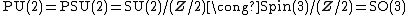
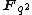, unique up to unitary congruence, and correspondingly a matrix group denoted 
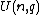or 
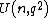, and likewise special and projective unitary groups. For convenience, this article with use the 
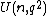convention.
Recall that the group of units of a finite field is cyclic, so the group of units of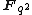
, and thus the group of invertible scalar matrices in 
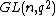, is the cyclic group of order 
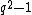. The center of 
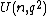has order 
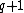and consists of the scalar matrices which are unitary, that is those matrices 
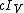with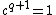 
. The center of the special unitary group has order 
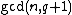and consists of those unitary scalars which also have order dividing 
.
The quotient of the unitary group by its center is the projective unitary group,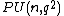
, and the quotient of the special unitary group by its center is the projective special unitary group 
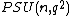. In most cases (
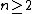and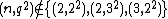 
), 
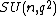is a perfect group
and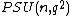
is a finite simple group
, .
.
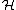Let U(H) denote the space of unitary operators on an infinite-dimensional Hilbert space. When f: X → U(H) is a continuous mapping of a compact space X into the unitary group, one can use a finite dimensional approximation of its image and a simple K-theoretic tric
to show that it is actually homotopic to the trivial map onto a single point. This means that U(H) is weakly contractible, and an additional argument shows that it is actually contractible. Note that this is a purely infinite dimensional phenomenon, in contrast to the finite-dimensional cousins U(n) and their limit U(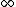
) under the inclusion maps which are not contractible admitting homotopically nontrivial continuous mappings onto U(1) given by the determinant of matrices.
The center of the infinite-dimensional unitary group U(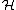
) is, as in the finite dimensional case, U(1), which again acts on the unitary group via multiplication by a phase. As the unitary group does not contain the zero matrix, this action is free. Thus U(
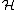) is a contractible space with a U(1) action, which identifies it as EU(1) and the space of U(1) orbits as BU(1), the classifying space
for U(1).
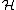) is defined precisely to be the space of orbits of the U(1) action on U(
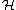), thus PU(
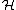) is a realization of the classifying space BU(1). In particular, using the isomorphism
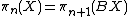
between the homotopy group
s of a space X and the homotopy groups of its classifying space BX, combined with the homotopy type of the circle U(1)
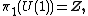
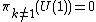
we find the homotopy groups of PU(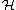
)
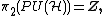
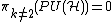
thus identifying PU(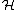
) as a representative of the Eilenberg–MacLane space K(Z,2).
As a consequence, PU(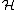
) must be of the same homotopy type as the infinite-dimensional complex projective space
, which also represents K(Z,2). This means in particular that they have isomorphic homology
and cohomology
groups
and
PU(n) has an adjoint action on SU(n), thus it has an (n2-1)-dimensional representation. When n=2 this corresponds to the three dimensional representation of SO(3). The adjoint action is defined by thinking of an element of PU(n) as an equivalence class of elements of U(n) that differ by phases. One can then take the adjoint action with respect to any of these U(n) representatives, and the phases commute with everything and so cancel. Thus the action is independent of the choice of representative and so it is well-defined.
, which is a representation up to a phase which is independent of the vector on which one acts. These are useful in quantum mechanics, as physical states are only defined up to phase. For example, massive fermionic states transform under a projective representation but not under a representation of the little group PU(2)=SO(3).
The projective representations of a group are classified by its second integral cohomology
, which in this case is
The cohomology groups in the finite case can be derived from the long exact sequence for bundles and the above fact that SU(n) is a Z/n bundle over PU(n). The cohomology in the infinite case was argued above from the isomorphism with the cohomology of the infinite complex projective space.
Thus PU(n) enjoys n projective representations, of which the first is the fundamental representation of its SU(n) cover, while PU(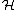
) has a countably infinite number. As usual, the projective representations of a group are ordinary representations of a central extension of the group. In this case the central extended group corresponding to the first projective representation of each projective unitary group is just the original unitary group
that we quotiented by U(1) in the definition of PU.
. Here the adjoint action of the infinite-dimensional PU(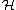
) on either the Fredholm operator
s or the infinite unitary group
is used.
In geometrical constructions of twisted K-theory with twist H, the PU(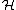
) is the fiber of a bundle, and different twists H correspond to different fibrations. As seen below, topologically PU(
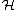) represents the Eilenberg–Maclane space K(Z,2), therefore the classifying space of PU(
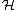) bundles is the Eilenberg–Maclane space K(Z,3). K(Z,3) is also the classifying space for the third integral cohomology
group, therefore PU(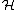
) bundles are classified by the third integral cohomology. As a result, the possible twists H of a twisted K-theory are precisely the elements of the third integral cohomology.
, which is a gauge theory with only gluon
s and no fundamental matter, all fields transform in the adjoint of the gauge group SU(n). The Z/n center of SU(n) commutes, being in the center, with SU(n)-valued fields and so the adjoint action of the center is trivial. Therefore the gauge symmetry is the quotient of SU(n) by Z/n, which is PU(n) and it acts on fields using the adjoint action described above.
In this context, the distinction between SU(n) and PU(n) has an important physical consequence. SU(n) is simply connected, but the fundamental group of PU(n) is Z/n, the cyclic group of order n. Therefore a PU(n) gauge theory with adjoint scalars will have nontrivial codimension 2 vortices
in which the expectation values of the scalars wind around PU(n)'s nontrivial cycle as one encircles the vortex. These vortices, therefore, also have charges in Z/n, which implies that they attract each other and when n come into contact they annihilate. An example of such a vortex is the Douglas–Shenker string in SU(n) Seiberg–Witten gauge theories.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the projective unitary group PU(n) is the quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n) by the right multiplication of its center, U(1), embedded as scalars.
Abstractly, it is the holomorphic isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, just as the projective orthogonal group
Projective orthogonal group
In projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...
is the isometry group of real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
.
In terms of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, elements of U(n) are complex n
n unitary matrices, and elements of the center are diagonal matrices equal to 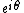multiplied by the identity matrix. Thus elements of PU(n) correspond to equivalence classes of unitary matrices under multiplication by a constant phase 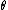.Abstractly, given a Hermitian space V, the group PU(V) is the image of the unitary group U(V) in the automorphism group of the projective space
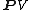.Projective special unitary group
The projective special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
PSU(n) is equal to the projective unitary group, in contrast to the orthogonal case.
The connections between the U(n), SU(n), their centers, and the projective unitary groups is shown at right.
The center of the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
is the scalar matrices of the nth roots of unity:
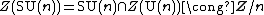
The natural map
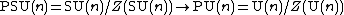
is an isomorphism, by the second isomorphism theorem, thus
- PU(n) = PSU(n) = SU(n)/(Z/n).
and the special unitary group SU(n) is an n-fold cover of the projective unitary group.
Examples
At n = 1, U(1) is abelian and so is equal to its center. Therefore PU(1) = U(1)/U(1) is a trivial groupTrivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
.
At n = 2,
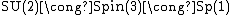, all being representable by unit norm quaternions, and 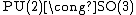, via: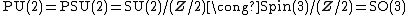Finite fields
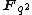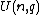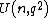One can also define unitary groups over finite fields: given a field of order q, there is a non-degenerate Hermitian structure on vector spaces over, unique up to unitary congruence, and correspondingly a matrix group denoted or , and likewise special and projective unitary groups. For convenience, this article with use the 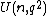convention.Recall that the group of units of a finite field is cyclic, so the group of units of
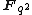, and thus the group of invertible scalar matrices in 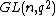, is the cyclic group of order 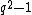. The center of 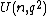has order 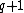and consists of the scalar matrices which are unitary, that is those matrices 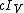with 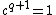. The center of the special unitary group has order 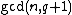and consists of those unitary scalars which also have order dividing .The quotient of the unitary group by its center is the projective unitary group,
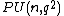, and the quotient of the special unitary group by its center is the projective special unitary group 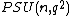. In most cases ( 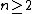and 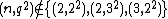), 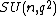is a perfect groupPerfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
and
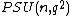is a finite simple groupSimple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, .
PU(H) is a classifying space for circle bundles
The same construction may be applied to matrices acting on an infinite-dimensional Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
.Let U(H) denote the space of unitary operators on an infinite-dimensional Hilbert space. When f: X → U(H) is a continuous mapping of a compact space X into the unitary group, one can use a finite dimensional approximation of its image and a simple K-theoretic tric
to show that it is actually homotopic to the trivial map onto a single point. This means that U(H) is weakly contractible, and an additional argument shows that it is actually contractible. Note that this is a purely infinite dimensional phenomenon, in contrast to the finite-dimensional cousins U(n) and their limit U(
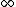) under the inclusion maps which are not contractible admitting homotopically nontrivial continuous mappings onto U(1) given by the determinant of matrices.The center of the infinite-dimensional unitary group U(
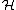) is, as in the finite dimensional case, U(1), which again acts on the unitary group via multiplication by a phase. As the unitary group does not contain the zero matrix, this action is free. Thus U(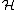) is a contractible space with a U(1) action, which identifies it as EU(1) and the space of U(1) orbits as BU(1), the classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for U(1).
The homotopy and (co)homology of PU(H)
PU(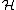) is defined precisely to be the space of orbits of the U(1) action on U(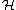), thus PU(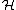) is a realization of the classifying space BU(1). In particular, using the isomorphism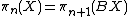between the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of a space X and the homotopy groups of its classifying space BX, combined with the homotopy type of the circle U(1)
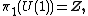
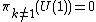
we find the homotopy groups of PU(
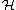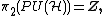
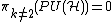
) thus identifying PU(
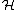) as a representative of the Eilenberg–MacLane space K(Z,2).As a consequence, PU(
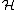) must be of the same homotopy type as the infinite-dimensional complex projective spaceComplex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, which also represents K(Z,2). This means in particular that they have isomorphic homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
groups
- H2n(PU(
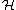))=H2n(PU(
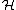))=Z
and
- H2n+1(PU(
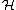))=H2n+1(PU(
))=0.
The adjoint representation
PU(n) in general has no n-dimensional representations, just as SO(3) has no two-dimensional representations.PU(n) has an adjoint action on SU(n), thus it has an (n2-1)-dimensional representation. When n=2 this corresponds to the three dimensional representation of SO(3). The adjoint action is defined by thinking of an element of PU(n) as an equivalence class of elements of U(n) that differ by phases. One can then take the adjoint action with respect to any of these U(n) representatives, and the phases commute with everything and so cancel. Thus the action is independent of the choice of representative and so it is well-defined.
Projective representations
In many applications PU(n) does not act in any linear representation, but instead in a projective representationProjective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
, which is a representation up to a phase which is independent of the vector on which one acts. These are useful in quantum mechanics, as physical states are only defined up to phase. For example, massive fermionic states transform under a projective representation but not under a representation of the little group PU(2)=SO(3).
The projective representations of a group are classified by its second integral cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
, which in this case is
- H2(PU(n)) = Z/n or H2(PU(
)) = Z.
The cohomology groups in the finite case can be derived from the long exact sequence for bundles and the above fact that SU(n) is a Z/n bundle over PU(n). The cohomology in the infinite case was argued above from the isomorphism with the cohomology of the infinite complex projective space.
Thus PU(n) enjoys n projective representations, of which the first is the fundamental representation of its SU(n) cover, while PU(
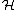) has a countably infinite number. As usual, the projective representations of a group are ordinary representations of a central extension of the group. In this case the central extended group corresponding to the first projective representation of each projective unitary group is just the original unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
that we quotiented by U(1) in the definition of PU.
Twisted K-theory
The adjoint action of the infinite projective unitary group is useful in geometric definitions of twisted K-theoryTwisted K-theory
In mathematics, twisted K-theory is a variation on K-theory, a mathematical theory from the 1950s that spans algebraic topology, abstract algebra and operator theory....
. Here the adjoint action of the infinite-dimensional PU(
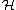) on either the Fredholm operatorFredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
s or the infinite unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
is used.
In geometrical constructions of twisted K-theory with twist H, the PU(
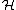) is the fiber of a bundle, and different twists H correspond to different fibrations. As seen below, topologically PU(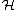) represents the Eilenberg–Maclane space K(Z,2), therefore the classifying space of PU() bundles is the Eilenberg–Maclane space K(Z,3). K(Z,3) is also the classifying space for the third integral cohomologyCohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
group, therefore PU(
) bundles are classified by the third integral cohomology. As a result, the possible twists H of a twisted K-theory are precisely the elements of the third integral cohomology.Pure Yang–Mills gauge theory
In the pure Yang–Mills SU(n) gauge theoryGauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, which is a gauge theory with only gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s and no fundamental matter, all fields transform in the adjoint of the gauge group SU(n). The Z/n center of SU(n) commutes, being in the center, with SU(n)-valued fields and so the adjoint action of the center is trivial. Therefore the gauge symmetry is the quotient of SU(n) by Z/n, which is PU(n) and it acts on fields using the adjoint action described above.
In this context, the distinction between SU(n) and PU(n) has an important physical consequence. SU(n) is simply connected, but the fundamental group of PU(n) is Z/n, the cyclic group of order n. Therefore a PU(n) gauge theory with adjoint scalars will have nontrivial codimension 2 vortices
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
in which the expectation values of the scalars wind around PU(n)'s nontrivial cycle as one encircles the vortex. These vortices, therefore, also have charges in Z/n, which implies that they attract each other and when n come into contact they annihilate. An example of such a vortex is the Douglas–Shenker string in SU(n) Seiberg–Witten gauge theories.
See also
- unitary groupUnitary groupIn mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
- special unitary groupSpecial unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
- unitary operators
- projective orthogonal groupProjective orthogonal groupIn projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...