R-algebroid
Encyclopedia
In mathematics
, R-algebroids are constructed starting from groupoid
s. These are more abstract concepts than the Lie algebroid
s that play a similar role in the theory of Lie groupoid
s to that of Lie algebra
s in the theory of Lie group
s. (Thus, a Lie algebroid
can be thought of as 'a Lie algebra
with many objects ').
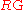, is constructed as follows. The object set of 
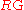is the same as that of 
and 
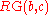is the free
R-module on the set
, with composition given by the usual bilinear rule, extending the composition of 
.
in this construction with a general category
C (that does not have all morphisms invertible).
, to be the set of functions 
with finite support, and with the convolution
product defined as follows:
.
Only this second construction is natural for the topological case, when one needs to replace 'function
' by 'continuous function
with compact support', and in this case
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, R-algebroids are constructed starting from groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
s. These are more abstract concepts than the Lie algebroid
Lie algebroid
In mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
s that play a similar role in the theory of Lie groupoid
Lie groupoid
In mathematics, a Lie groupoid is a groupoid where the set Ob of objects and the set Mor of morphisms are both manifolds, the source and target operationss,t : Mor \to Ob...
s to that of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s in the theory of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. (Thus, a Lie algebroid
Lie algebroid
In mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
can be thought of as 'a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
with many objects ').
Definition
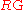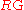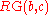An R-algebroid,, is constructed as follows. The object set of is the same as that of and is the freeFree module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
R-module on the set
, with composition given by the usual bilinear rule, extending the composition of .R-category
More generally, an R-category is defined as an extension of this R-algebroid concept by replacing the groupoid in this construction with a general categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C (that does not have all morphisms invertible).
R-algebroids via convolution products
One can also define the R-algebroid,, to be the set of functions with finite support, and with the convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
product defined as follows:
.Only this second construction is natural for the topological case, when one needs to replace 'function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
' by 'continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
with compact support', and in this case
.Examples
- Every Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is a Lie algebroid over the one point manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. - The Lie algebroid associated to a Lie groupoidLie groupoidIn mathematics, a Lie groupoid is a groupoid where the set Ob of objects and the set Mor of morphisms are both manifolds, the source and target operationss,t : Mor \to Ob...
.
See also
- Higher-dimensional algebraHigher-dimensional algebraSupercategories were first introduced in 1970, and were subsequently developed for applications in theoretical physics and mathematical biology or mathematical biophysics....
- AlgebroidAlgebroidIn mathematics, algebroid may mean*algebroid branch, a formal power series branch of an algebraic curve*algebroid multifunction*Lie algebroid in the theory of Lie groupoids*algebroid cohomology...
- Ring (mathematics)Ring (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
- Convolution productConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
- Module (mathematics)Module (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
- GroupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
- Double groupoidDouble groupoidIn mathematics, especially in higher-dimensional algebra and homotopy theory, a double groupoid generalises the notion of groupoid and of category to a higher dimension.- Definition :...
- Crossed moduleCrossed moduleIn mathematics, and especially in homotopy theory, a crossed module consists of groups G and H, where G acts on H , and a homomorphism of groups...
- Algebraic category
- Lie groupoidLie groupoidIn mathematics, a Lie groupoid is a groupoid where the set Ob of objects and the set Mor of morphisms are both manifolds, the source and target operationss,t : Mor \to Ob...
s - Lie algebroidLie algebroidIn mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
s - BialgebraBialgebraIn mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
- Hopf algebraHopf algebraIn mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
- Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
- Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
- BicategoryBicategoryIn mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.Formally, a bicategory B...