Real closed ring
Encyclopedia
In mathematics
, a real closed ring is a commutative ring
A that
is a subring of a product of real closed field
s, which is closed under
continuous semi-algebraic
functions defined over the integers.
The link to the definition at the beginning of this article is given in the section on algebraic properties below.
homomorphism over R. This means that rcl(R) is a real closed ring and there is a (not necessarily injective) ring homomorphism
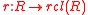such that for every ring homomorphism 
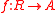to some other real closed ring A, there is a unique ring homomorphism 
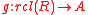with 
.
For example the real closure of the polynomial ring
is the ring of continuous semi-algbebraic functions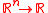
.
Note that an arbitrary ring R is semi-real (i.e. -1 is not a sum of squares in R)
if and only if the real closure of R is not the null ring.
Note also that the real closure of an ordered field
is in general not the real closure of the underlying field. For example, the real closure of the ordered subfield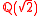
of
is the field 
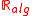of real algebraic numbers,
whereas the real closure of the field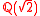
is the ring
(corresponding to the two orders of 
). More generally the real closure of a field F
is a certain subdirect product of the real closures of the ordered fields (F,P), where P runs through the orderings of F.
atizable and undecidable
. The class of all real closed valuation rings is decidable
(by Cherlin-Dickmann) and the class of all real closed fields is decidable (by Tarski). After naming a definable radical relation, real closed rings have a model companion
, namely von Neumann regular real closed rings.
. For example
in terms of maximality (with respect to algebraic extensions): a real closed field is a maximally orderable field; or, a real closed field (together with its unique ordering) is a maximally ordered field. Another characterization says that the intermediate value theorem holds for all polynomials in one variable over the (ordered) field. In the case of commutative rings, all these properties can be (and are) analyzed in the literature. They all lead to different classes of rings which are unfortunately also called 'real closed' (because a certain characterization of real closed fields has been extended to rings). None of them lead to the class of real closed rings and none of them allow a satisfactory notion of a closure operation. A central point in the definition of real closed rings is the globalisation of the notion of a real closed field to rings when these rings are represented as rings of functions on some space (typically, the real spectrum of the ring).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a real closed ring is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
A that
is a subring of a product of real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s, which is closed under
continuous semi-algebraic
Semialgebraic set
In mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
functions defined over the integers.
Examples of real closed rings
Since the rigorous definition of a real closed ring is of technical nature it is convenient to see a list of prominent examples first. The following rings are all real closed rings:- real closed fieldReal closed fieldIn mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s. These are exactly the real closed rings that are fields. - the ring of all real valued continuous functions on a completely regular space X. Also, the ring of all bounded real valued continuous functions on X is real closed.
- convex subrings of real closed fields. These are precisely those real closed rings which are also valuation ringValuation ringIn abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
s and were initially studied by Cherlin and Dickmann (they used the term 'real closed ring' for what is now called 'real closed valuation ring'). - the ring A of all continuous semi-algebraic functionSemialgebraic setIn mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
s on a semi-algebraic set of a real closed field (with values in that field). Also, the subring of all bounded (in any sense) functions in A is real closed. - (generalizing the previous example) the ring of all (bounded) continuous definable functions on a definable setDefinable setIn mathematical logic, a definable set is an n-ary relation on the domain of a structure whose elements are precisely those elements satisfying some formula in the language of that structure...
S of an arbitrary first-order expansion M of a real closed field (with values in M). Also, the ring of all (bounded) definable functions
is real closed. - Real closed rings are precisely the rings of global sections of affine real closed spaces (a generalization of semialgebraic spaceSemialgebraic spaceIn mathematics, especially in real algebraic geometry, a semialgebraic space is a space which is locally isomorphic to a semialgebraic set.-Definition:Let U be an open subset of Rn for some n...
s) and in this context they were invented by Niels Schwartz in the early 1980s.
Definition
A real closed ring is a reduced, commutative unital ring A which has the following properties:- The set of squares of A is the set of nonnegative elements of a partial order ≤ on A and (A,≤) is an f-ring.
- Convexity condition: For all a,b from A, if 0≤a≤b then b|a2.
- For every prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
p of A, the residue class ring A/p is integrally closedIntegrally closedIn mathematics, more specifically in abstract algebra, the concept of integrally closed has two meanings, one for groups and one for rings. -Commutative rings:...
and its field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
is a real closed field.
The link to the definition at the beginning of this article is given in the section on algebraic properties below.
The real closure of a commutative ring
Every commutative unital ring R has a so called real closure rcl(R) and this is unique up to a unique ringhomomorphism over R. This means that rcl(R) is a real closed ring and there is a (not necessarily injective) ring homomorphism
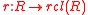such that for every ring homomorphism 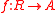to some other real closed ring A, there is a unique ring homomorphism 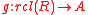with .For example the real closure of the polynomial ring
is the ring of continuous semi-algbebraic functions
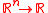.Note that an arbitrary ring R is semi-real (i.e. -1 is not a sum of squares in R)
if and only if the real closure of R is not the null ring.
Note also that the real closure of an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
is in general not the real closure of the underlying field. For example, the real closure of the ordered subfield
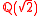
of
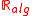is the field of real algebraic numbers,whereas the real closure of the field
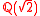is the ring (corresponding to the two orders of ). More generally the real closure of a field Fis a certain subdirect product of the real closures of the ordered fields (F,P), where P runs through the orderings of F.
Algebraic properties
- The categoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
RCR of real closed rings which has real closed rings as objects and ring homomorphisms as maps has the following properties:
- Arbitrary products, direct limits and inverse limits (in the category of commutative unital rings) of real closed rings are again real closed. The fibre sumPushout (category theory)In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
of two real closed rings B,C over some real closed ring A exists in RCR and is the real closure of the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of B and C over A. - RCR has arbitrary limits and co-limits.
- RCR is a varietyVariety (universal algebra)In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
in the sense of universal algebraUniversal algebraUniversal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
(but not a subvariety of commutative rings).- For a real closed ring A, the natural homomorphism of A to the product of all its residue fieldResidue fieldIn mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
s is an isomorphism onto a subring of this product that is closed under continuous semi-algebraicSemialgebraic setIn mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
functions defined over the integers. Conversely, every subring of a product of real closed fields with this property is real closed. - If I is a radical ideal of a real closed ring A, then also the residue class ring A/I is real closed. If I and J are radical ideals of a real closed ring then the sum I + J is again a radical ideal.
- All classical localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
s S−1A of a real closed ring A are real closed. The epimorphic hull and the complete ring of quotients of a real closed ring are again real closed. - The (real) holomorphy ring H(A) of a real closed ring A is again real closed. By definition, H(A) consists of all elements f in A with the property −N ≤ f ≤ N for some natural number N. Applied to the examples above, this means that the rings of bounded (semi-algberaic/definable) continuous functions are all real closed.
- The support map from the real spectrum of a real closed ring to its Zariski spectrumSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
, which sends an ordering P to its support
is an homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. In particular, the Zariski spectrum of every real closed ring A is a root system (in the sense of graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
) and therefore A is also a Gel'fand ring (i.e. every prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
of A is contained in a unique maximal ideal of A). The comparison of the Zariski spectrum of A with the Zariski spectrum of H(A) leads to a homeomorphism between the maximal spectra of these rings, generalizing the Gel'fand-Kolmogorov theorem for rings of real valued continuous functions. - The natural map r from an arbitrary ring R to its real closure rcl(R) as explained above, induces a homeomorphism from the real spectrum of rcl(R) to the real spectrum of R.
- Summarising and significantly strengthening the previous two properties, the following is true: The natural map r from an arbitrary ring R to its real closure rcl(R) induces an identification of the affine scheme of rcl(R) with the affine real closed space of R.
- For a real closed ring A, the natural homomorphism of A to the product of all its residue field
Model theoretic properties
The class of real closed rings is first-order axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atizable and undecidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
. The class of all real closed valuation rings is decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
(by Cherlin-Dickmann) and the class of all real closed fields is decidable (by Tarski). After naming a definable radical relation, real closed rings have a model companion
Model complete theory
In model theory, a first-order theory is called model complete if every embedding of models is an elementary embedding.Equivalently, every first-order formula is equivalent to a universal formula.This notion was introduced by Abraham Robinson....
, namely von Neumann regular real closed rings.
Comparison with characterizations of real closed fields
There are many different characterizations of real closed fieldsReal closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
. For example
in terms of maximality (with respect to algebraic extensions): a real closed field is a maximally orderable field; or, a real closed field (together with its unique ordering) is a maximally ordered field. Another characterization says that the intermediate value theorem holds for all polynomials in one variable over the (ordered) field. In the case of commutative rings, all these properties can be (and are) analyzed in the literature. They all lead to different classes of rings which are unfortunately also called 'real closed' (because a certain characterization of real closed fields has been extended to rings). None of them lead to the class of real closed rings and none of them allow a satisfactory notion of a closure operation. A central point in the definition of real closed rings is the globalisation of the notion of a real closed field to rings when these rings are represented as rings of functions on some space (typically, the real spectrum of the ring).