
Reciprocity (electromagnetism)
Encyclopedia
In classical electromagnetism
, reciprocity refers to a variety of related theorems involving the interchange of time-harmonic
electric current densities
(sources) and the resulting electromagnetic field
s in Maxwell's equations
for time-invariant linear media under certain constraints. Reciprocity is closely related to the concept of Hermitian operators from linear algebra
, applied to electromagnetism.
Perhaps the most common and general such theorem is Lorentz reciprocity (and its various special cases such as Rayleigh-Carson reciprocity), named after work by Hendrik Lorentz
in 1896 following analogous results regarding sound
by Lord Rayleigh and Helmholtz (Potton, 2004). Loosely, it states that the relationship between an oscillating current and the resulting electric field
is unchanged if one interchanges the points where the current is placed and where the field is measured. For the specific case of an electrical network
, it is sometimes phrased as the statement that voltage
s and currents at different points in the network can be interchanged. More technically, it follows that the mutual impedance of a first circuit due to a second is the same as the mutual impedance of the second circuit due to the first.
There is also an analogous theorem in electrostatics
, known as Green's reciprocity, relating the interchange of electric potential
and electric charge density.
Forms of the reciprocity theorems are used in many electromagnetic applications, such as analyzing electrical networks and antenna
systems. For example, reciprocity implies that antennas work equally well as transmitters or receivers, and specifically that an antenna's radiation and receiving patterns
are identical. Reciprocity is also a basic lemma that is used to prove other theorems about electromagnetic systems, such as the symmetry of the impedance matrix
and scattering matrix
, symmetries of Green's function
s for use in boundary-element
and transfer-matrix computational methods, as well as orthogonality
properties of harmonic modes in waveguide
systems (as an alternative to proving those properties directly from the symmetries of the eigen-operators
).
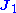 that produces an electric field
that produces an electric field
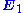 and a magnetic field
and a magnetic field
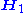 , where all three are periodic functions of time with angular frequency
, where all three are periodic functions of time with angular frequency
ω, and in particular they have time-dependence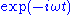 . Suppose that we similarly have a second current
. Suppose that we similarly have a second current 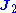 at the same frequency ω which (by itself) produces fields
at the same frequency ω which (by itself) produces fields 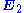 and
and 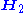 . The Lorentz reciprocity theorem then states, under certain simple conditions on the materials of the medium described below, that for an arbitrary surface S enclosing a volume V:
. The Lorentz reciprocity theorem then states, under certain simple conditions on the materials of the medium described below, that for an arbitrary surface S enclosing a volume V:
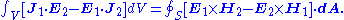
Equivalently, in differential form (by the divergence theorem
):
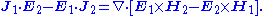
This general form is commonly simplified for a number of special cases. In particular, one usually assumes that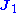 and
and 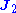 are localized (i.e. have compact support), and that there are no incoming waves from infinitely far away. In this case, if one integrates over all space then the surface-integral terms cancel (see below) and one obtains:
are localized (i.e. have compact support), and that there are no incoming waves from infinitely far away. In this case, if one integrates over all space then the surface-integral terms cancel (see below) and one obtains:

This result (along with the following simplifications) is sometimes called the Rayleigh-Carson reciprocity theorem, after Lord Rayleigh's work on sound waves and an extension by John R. Carson (1924; 1930) to applications for radio frequency
antennas. Often, one further simplifies this relation by considering point-like dipole
sources, in which case the integrals disappear and one simply has the product of the electric field with the corresponding dipole moments of the currents. Or, for wires of negligible thickness, one obtains the applied current in one wire multiplied by the resulting voltage across another and vice versa; see also below.
Another special case of the Lorentz reciprocity theorem applies when the volume V entirely contains both of the localized sources (or alternatively if V intersects neither of the sources). In this case:

(i.e. currents that respond linearly to the applied field) with a 3×3 conductivity matrix σ that is required to be symmetric, which is implied by the other conditions below. In order to properly describe this situation, one must carefully distinguish between the externally applied fields (from the driving voltages) and the total fields that result (King, 1963).
More specifically, the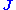 above only consisted of external "source" terms introduced into Maxwell's equations. We now denote this by
above only consisted of external "source" terms introduced into Maxwell's equations. We now denote this by 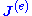 to distinguish it from the total current produced by both the external source and by the resulting electric fields in the materials. If this external current is in a material with a conductivity σ, then it corresponds to an externally applied electric field
to distinguish it from the total current produced by both the external source and by the resulting electric fields in the materials. If this external current is in a material with a conductivity σ, then it corresponds to an externally applied electric field 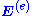 where, by definition of σ:
where, by definition of σ:
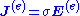
Moreover, the electric field above only consisted of the response to this current, and did not include the "external" field
above only consisted of the response to this current, and did not include the "external" field 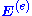 . Therefore, we now denote the field from before as
. Therefore, we now denote the field from before as 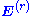 , where the total field is given by
, where the total field is given by  .
.
Now, the equation on the left-hand side of the Lorentz reciprocity theorem can be rewritten by moving the σ from the external current term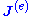 to the response field terms
to the response field terms  , and also adding and subtracting a
, and also adding and subtracting a 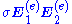 term, to obtain the external field multiplied by the total current
term, to obtain the external field multiplied by the total current 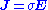 :
:
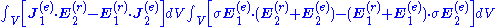
For the limit of thin wires, this gives the product of the externally applied voltage (1) multiplied by the resulting total current (2) and vice versa. In particular, the Rayleigh-Carson reciprocity theorem becomes a simple summation:
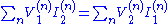
where V and I denote the (complex) amplitudes of the AC
applied voltages and the resulting currents, respectively, in a set of circuit elements (indexed by n) for two possible sets of voltages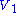 and
and 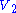 .
.
Most commonly, this is simplified further to the case where each system has a single voltage source V, at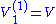 and
and 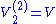 . Then the theorem becomes simply
. Then the theorem becomes simply 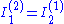 : the current at position (1) from a voltage at (2) is identical to the current at (2) from the same voltage at (1).
: the current at position (1) from a voltage at (2) is identical to the current at (2) from the same voltage at (1).
 relating
relating 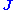 and
and  at a fixed frequency (in linear media):
at a fixed frequency (in linear media):
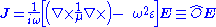
is usually a Hermitian operator under the inner product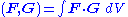 for vector field
for vector field
s and
and  . (Technically, this unconjugated
. (Technically, this unconjugated
form is not a true inner product because it is not real-valued for complex-valued fields, but that is not a problem here. In this sense, the operator is not truly Hermitian but is rather complex-symmetric.) This is true whenever the permittivity
ε and the magnetic permeability μ, at the given ω, are symmetric 3×3 matrices (symmetric rank-2 tensors) — this includes the common case where they are scalar
s (for isotropic media), of course. They need not be real—complex values correspond to materials with losses, such as conductors with finite conductivity σ (which is included in ε via )—and because of this the reciprocity theorem does not require time reversal invariance. The condition of symmetric ε and μ matrices is almost always satisfied; see below for an exception.
)—and because of this the reciprocity theorem does not require time reversal invariance. The condition of symmetric ε and μ matrices is almost always satisfied; see below for an exception.
For any Hermitian operator under an inner product
under an inner product 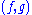 , we have
, we have  by definition, and the Rayleigh-Carson reciprocity theorem is merely the vectorial version of this statement for this particular operator
by definition, and the Rayleigh-Carson reciprocity theorem is merely the vectorial version of this statement for this particular operator 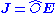 : that is,
: that is,  . The Hermitian property of the operator here can be derived by integration by parts
. The Hermitian property of the operator here can be derived by integration by parts
. For a finite integration volume, the surface terms from this integration by parts yield the more-general surface-integral theorem above. In particular, the key fact is that, for vector fields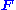 and
and  , integration by parts (or the divergence theorem
, integration by parts (or the divergence theorem
) over a volume V enclosed by a surface S gives the identity:
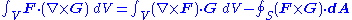
This identity is then applied twice to to yield
to yield 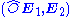 plus the surface term, giving the Lorentz reciprocity relation.
plus the surface term, giving the Lorentz reciprocity relation.
The simplest argument would be that the fields goes to zero at infinity for a localized source, but this argument fails in the case of lossless media: in the absence of absorption, radiated fields decay inversely with distance, but the surface area of the integral increases with the square of distance, so the two rates balance one another in the integral.
Instead, it is common (e.g. King, 1963) to assume that the medium is homogeneous and isotropic sufficiently far away. In this case, the radiated field asymptotically takes the form of planewaves propagating radially outward (in the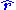 direction) with
direction) with 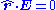 and
and 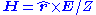 where Z is the impedance
where Z is the impedance
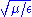 of the surrounding medium. Then it follows that
of the surrounding medium. Then it follows that 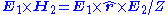 , which by a simple vector identity equals
, which by a simple vector identity equals 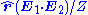 . Similarly,
. Similarly,  and the two terms cancel one another.
and the two terms cancel one another.
The above argument shows explicitly why the surface terms can cancel, but lacks generality. Alternatively, one can treat the case of lossless surrounding media by taking the limit as the losses (the imaginary part of ε) go to zero. For any nonzero loss, the fields decay exponentially with distance and the surface integral vanishes, regardless of whether the medium is homogeneous. Since the left-hand side of the Lorentz reciprocity theorem vanishes for integration over all space with any non-zero losses, it must also vanish in the limit as the losses go to zero. (Note that we implicitly assumed the standard boundary condition of zero incoming waves from infinity, because otherwise even an infinitesimal loss would eliminate the incoming waves and the limit would not give the lossless solution.)
 , i.e. in
, i.e. in  (which requires a specification of the boundary conditions at infinity in a lossless system), has the same symmetry as
(which requires a specification of the boundary conditions at infinity in a lossless system), has the same symmetry as  and is essentially a Green's function
and is essentially a Green's function
convolution
. So, another perspective on Lorentz reciprocity is that it reflects the fact that convolution with the electromagnetic Green's function is a complex-symmetric (or anti-Hermitian, below) linear operation under the appropriate conditions on ε and μ. More specifically, the Green's function can be written as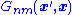 giving the n-th component of
giving the n-th component of  at
at 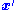 from a point dipole current in the m-th direction at
from a point dipole current in the m-th direction at  (essentially,
(essentially,  gives the matrix elements of
gives the matrix elements of 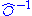 ), and Rayleigh-Carson reciprocity is equivalent to the statement that
), and Rayleigh-Carson reciprocity is equivalent to the statement that 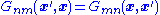 . Unlike
. Unlike  , it is not generally possible to give an explicit formula for the Green's function (except in special cases such as homogeneous media), but it is routinely computed by numerical methods.
, it is not generally possible to give an explicit formula for the Green's function (except in special cases such as homogeneous media), but it is routinely computed by numerical methods.
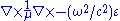 is Hermitian under the conjugated inner product
is Hermitian under the conjugated inner product 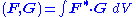 , and a variant of the reciprocity theorem still holds:
, and a variant of the reciprocity theorem still holds:
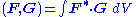
where the sign changes come from the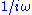 in the equation above, which makes the operator
in the equation above, which makes the operator  anti-Hermitian (neglecting surface terms). For the special case of
anti-Hermitian (neglecting surface terms). For the special case of  , this gives a re-statement of conservation of energy
, this gives a re-statement of conservation of energy
or Poynting's theorem
(since here we have assumed lossless materials, unlike above): the time-average rate of work done by the current (given by the real part of ) is equal to the time-average outward flux of power (the integral of the Poynting vector
) is equal to the time-average outward flux of power (the integral of the Poynting vector
). By the same token, however, the surface terms do not in general vanish if one integrates over all space for this reciprocity variant, so a Rayleigh-Carson form does not hold without additional assumptions.
The fact that magneto-optic materials break Rayleigh-Carson reciprocity is the key to devices such as Faraday isolators and circulator
s. A current on one side of a Faraday isolator produces a field on the other side but not vice-versa.
 and
and 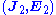 to exist in different systems.
to exist in different systems.
In particular, if satisfy Maxwell's equations at ω for a system with materials
satisfy Maxwell's equations at ω for a system with materials 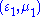 , and
, and 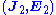 satisfy Maxwell's equations at ω for a system with materials
satisfy Maxwell's equations at ω for a system with materials 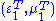 , where T denotes the transpose
, where T denotes the transpose
, then the equation of Lorentz reciprocity holds.
, no reciprocity theorem generally holds. Reciprocity also does not generally apply for time-varying ("active") media; for example, when ε is modulated in time by some external process. (In both of these cases, the frequency ω is not generally a conserved quantity.)
s:
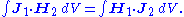
However, the Feld-Tai lemma is only valid under much more restrictive conditions than Lorentz reciprocity. It generally requires time-invariant linear media with an isotropic homogeneous impedance
, i.e. a constant scalar
μ/ε ratio, with the possible exception of regions of perfectly conducting material.
More precisely, Feld-Tai reciprocity requires the Hermitian (or rather, complex-symmetric) symmetry of the electromagnetic operators as above, but also relies on the assumption that the operator relating and
and 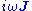 is a constant scalar multiple of the operator relating
is a constant scalar multiple of the operator relating  and
and 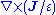 , which is true when ε is a constant scalar multiple of μ (the two operators generally differ by an interchange of ε and μ). As above, one can also construct a more general formulation for integrals over a finite volume.
, which is true when ε is a constant scalar multiple of μ (the two operators generally differ by an interchange of ε and μ). As above, one can also construct a more general formulation for integrals over a finite volume.
(Panofsky and Phillips, 1962).
In particular, let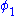 denote the electric potential resulting from a total charge density
denote the electric potential resulting from a total charge density 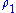 . The electric potential satisfies Poisson's equation
. The electric potential satisfies Poisson's equation
,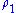 , where
, where 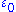 is the vacuum permittivity. Similarly, let
is the vacuum permittivity. Similarly, let  denote the electric potential resulting from a total charge density
denote the electric potential resulting from a total charge density 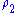 , satisfying
, satisfying 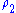 . In both cases, we assume that the charge distributions are localized, so that the potentials can be chosen to go to zero at infinity. Then, Green's reciprocity theorem states that, for integrals over all space:
. In both cases, we assume that the charge distributions are localized, so that the potentials can be chosen to go to zero at infinity. Then, Green's reciprocity theorem states that, for integrals over all space:
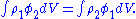
This theorem is easily proven from Green's second identity. Equivalently, it is the statement that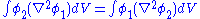 , i.e. that
, i.e. that  is a Hermitian operator (as follows by integrating by parts twice).
is a Hermitian operator (as follows by integrating by parts twice).
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, reciprocity refers to a variety of related theorems involving the interchange of time-harmonic
Harmonic (mathematics)
In mathematics, a number of concepts employ the word harmonic. The similarity of this terminology to that of music is not accidental: the equations of motion of vibrating strings, drums and columns of air are given by formulas involving Laplacians; the solutions to which are given by eigenvalues...
electric current densities
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
(sources) and the resulting electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
s in Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for time-invariant linear media under certain constraints. Reciprocity is closely related to the concept of Hermitian operators from linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, applied to electromagnetism.
Perhaps the most common and general such theorem is Lorentz reciprocity (and its various special cases such as Rayleigh-Carson reciprocity), named after work by Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
in 1896 following analogous results regarding sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
by Lord Rayleigh and Helmholtz (Potton, 2004). Loosely, it states that the relationship between an oscillating current and the resulting electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
is unchanged if one interchanges the points where the current is placed and where the field is measured. For the specific case of an electrical network
Electrical network
An electrical network is an interconnection of electrical elements such as resistors, inductors, capacitors, transmission lines, voltage sources, current sources and switches. An electrical circuit is a special type of network, one that has a closed loop giving a return path for the current...
, it is sometimes phrased as the statement that voltage
Voltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
s and currents at different points in the network can be interchanged. More technically, it follows that the mutual impedance of a first circuit due to a second is the same as the mutual impedance of the second circuit due to the first.
There is also an analogous theorem in electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, known as Green's reciprocity, relating the interchange of electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and electric charge density.
Forms of the reciprocity theorems are used in many electromagnetic applications, such as analyzing electrical networks and antenna
Antenna (radio)
An antenna is an electrical device which converts electric currents into radio waves, and vice versa. It is usually used with a radio transmitter or radio receiver...
systems. For example, reciprocity implies that antennas work equally well as transmitters or receivers, and specifically that an antenna's radiation and receiving patterns
Radiation pattern
In the field of antenna design the term radiation pattern most commonly refers to the directional dependence of the strength of the radio waves from the antenna or other source ....
are identical. Reciprocity is also a basic lemma that is used to prove other theorems about electromagnetic systems, such as the symmetry of the impedance matrix
Impedance parameters
Impedance parameters or Z-parameters are properties used in electrical engineering, electronic engineering, and communication systems engineering to describe the electrical behavior of linear electrical networks. They are also used to describe the small-signal response of non-linear networks...
and scattering matrix
Scattering parameters
Scattering parameters or S-parameters describe the electrical behavior of linear electrical networks when undergoing various steady state stimuli by electrical signals....
, symmetries of Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
s for use in boundary-element
Boundary element method
The boundary element method is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations . It can be applied in many areas of engineering and science including fluid mechanics, acoustics, electromagnetics, and fracture...
and transfer-matrix computational methods, as well as orthogonality
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
properties of harmonic modes in waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
systems (as an alternative to proving those properties directly from the symmetries of the eigen-operators
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
).
Lorentz reciprocity
Specifically, suppose that one has a current density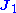 that produces an electric field
that produces an electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
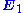 and a magnetic field
and a magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
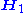 , where all three are periodic functions of time with angular frequency
, where all three are periodic functions of time with angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
ω, and in particular they have time-dependence
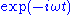 . Suppose that we similarly have a second current
. Suppose that we similarly have a second current 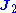 at the same frequency ω which (by itself) produces fields
at the same frequency ω which (by itself) produces fields 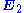 and
and 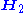 . The Lorentz reciprocity theorem then states, under certain simple conditions on the materials of the medium described below, that for an arbitrary surface S enclosing a volume V:
. The Lorentz reciprocity theorem then states, under certain simple conditions on the materials of the medium described below, that for an arbitrary surface S enclosing a volume V: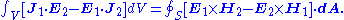
Equivalently, in differential form (by the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
):
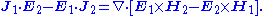
This general form is commonly simplified for a number of special cases. In particular, one usually assumes that
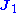 and
and 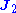 are localized (i.e. have compact support), and that there are no incoming waves from infinitely far away. In this case, if one integrates over all space then the surface-integral terms cancel (see below) and one obtains:
are localized (i.e. have compact support), and that there are no incoming waves from infinitely far away. In this case, if one integrates over all space then the surface-integral terms cancel (see below) and one obtains:
This result (along with the following simplifications) is sometimes called the Rayleigh-Carson reciprocity theorem, after Lord Rayleigh's work on sound waves and an extension by John R. Carson (1924; 1930) to applications for radio frequency
Radio frequency
Radio frequency is a rate of oscillation in the range of about 3 kHz to 300 GHz, which corresponds to the frequency of radio waves, and the alternating currents which carry radio signals...
antennas. Often, one further simplifies this relation by considering point-like dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
sources, in which case the integrals disappear and one simply has the product of the electric field with the corresponding dipole moments of the currents. Or, for wires of negligible thickness, one obtains the applied current in one wire multiplied by the resulting voltage across another and vice versa; see also below.
Another special case of the Lorentz reciprocity theorem applies when the volume V entirely contains both of the localized sources (or alternatively if V intersects neither of the sources). In this case:

Reciprocity for electrical networks
Above, Lorentz reciprocity was phrased in terms of an externally applied current source and the resulting field. Often, especially for electrical networks, one instead prefers to think of an externally applied voltage and the resulting currents. The Lorentz reciprocity theorem describes this case as well, assuming ohmic materialsOhm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
(i.e. currents that respond linearly to the applied field) with a 3×3 conductivity matrix σ that is required to be symmetric, which is implied by the other conditions below. In order to properly describe this situation, one must carefully distinguish between the externally applied fields (from the driving voltages) and the total fields that result (King, 1963).
More specifically, the
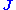 above only consisted of external "source" terms introduced into Maxwell's equations. We now denote this by
above only consisted of external "source" terms introduced into Maxwell's equations. We now denote this by 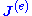 to distinguish it from the total current produced by both the external source and by the resulting electric fields in the materials. If this external current is in a material with a conductivity σ, then it corresponds to an externally applied electric field
to distinguish it from the total current produced by both the external source and by the resulting electric fields in the materials. If this external current is in a material with a conductivity σ, then it corresponds to an externally applied electric field 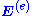 where, by definition of σ:
where, by definition of σ: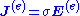
Moreover, the electric field
 above only consisted of the response to this current, and did not include the "external" field
above only consisted of the response to this current, and did not include the "external" field 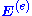 . Therefore, we now denote the field from before as
. Therefore, we now denote the field from before as 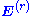 , where the total field is given by
, where the total field is given by  .
.Now, the equation on the left-hand side of the Lorentz reciprocity theorem can be rewritten by moving the σ from the external current term
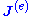 to the response field terms
to the response field terms  , and also adding and subtracting a
, and also adding and subtracting a 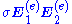 term, to obtain the external field multiplied by the total current
term, to obtain the external field multiplied by the total current 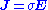 :
: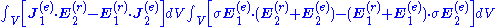
For the limit of thin wires, this gives the product of the externally applied voltage (1) multiplied by the resulting total current (2) and vice versa. In particular, the Rayleigh-Carson reciprocity theorem becomes a simple summation:
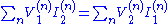
where V and I denote the (complex) amplitudes of the AC
Alternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
applied voltages and the resulting currents, respectively, in a set of circuit elements (indexed by n) for two possible sets of voltages
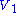 and
and 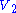 .
.Most commonly, this is simplified further to the case where each system has a single voltage source V, at
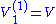 and
and 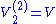 . Then the theorem becomes simply
. Then the theorem becomes simply 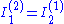 : the current at position (1) from a voltage at (2) is identical to the current at (2) from the same voltage at (1).
: the current at position (1) from a voltage at (2) is identical to the current at (2) from the same voltage at (1).Conditions and proof of Lorentz reciprocity
The Lorentz reciprocity theorem is simply a reflection of the fact that the linear operator relating
relating 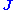 and
and  at a fixed frequency (in linear media):
at a fixed frequency (in linear media):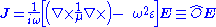
is usually a Hermitian operator under the inner product
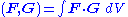 for vector field
for vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s
 and
and  . (Technically, this unconjugated
. (Technically, this unconjugatedComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
form is not a true inner product because it is not real-valued for complex-valued fields, but that is not a problem here. In this sense, the operator is not truly Hermitian but is rather complex-symmetric.) This is true whenever the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
ε and the magnetic permeability μ, at the given ω, are symmetric 3×3 matrices (symmetric rank-2 tensors) — this includes the common case where they are scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
s (for isotropic media), of course. They need not be real—complex values correspond to materials with losses, such as conductors with finite conductivity σ (which is included in ε via
 )—and because of this the reciprocity theorem does not require time reversal invariance. The condition of symmetric ε and μ matrices is almost always satisfied; see below for an exception.
)—and because of this the reciprocity theorem does not require time reversal invariance. The condition of symmetric ε and μ matrices is almost always satisfied; see below for an exception.For any Hermitian operator
 under an inner product
under an inner product 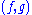 , we have
, we have  by definition, and the Rayleigh-Carson reciprocity theorem is merely the vectorial version of this statement for this particular operator
by definition, and the Rayleigh-Carson reciprocity theorem is merely the vectorial version of this statement for this particular operator 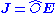 : that is,
: that is,  . The Hermitian property of the operator here can be derived by integration by parts
. The Hermitian property of the operator here can be derived by integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
. For a finite integration volume, the surface terms from this integration by parts yield the more-general surface-integral theorem above. In particular, the key fact is that, for vector fields
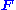 and
and  , integration by parts (or the divergence theorem
, integration by parts (or the divergence theoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
) over a volume V enclosed by a surface S gives the identity:
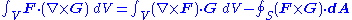
This identity is then applied twice to
 to yield
to yield 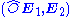 plus the surface term, giving the Lorentz reciprocity relation.
plus the surface term, giving the Lorentz reciprocity relation.Surface-term cancellation
The cancellation of the surface terms on the right-hand side of the Lorentz reciprocity theorem, for an integration over all space, is not entirely obvious but can be derived in a number of ways.The simplest argument would be that the fields goes to zero at infinity for a localized source, but this argument fails in the case of lossless media: in the absence of absorption, radiated fields decay inversely with distance, but the surface area of the integral increases with the square of distance, so the two rates balance one another in the integral.
Instead, it is common (e.g. King, 1963) to assume that the medium is homogeneous and isotropic sufficiently far away. In this case, the radiated field asymptotically takes the form of planewaves propagating radially outward (in the
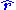 direction) with
direction) with 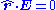 and
and 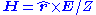 where Z is the impedance
where Z is the impedanceElectrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
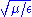 of the surrounding medium. Then it follows that
of the surrounding medium. Then it follows that 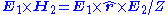 , which by a simple vector identity equals
, which by a simple vector identity equals 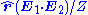 . Similarly,
. Similarly,  and the two terms cancel one another.
and the two terms cancel one another.The above argument shows explicitly why the surface terms can cancel, but lacks generality. Alternatively, one can treat the case of lossless surrounding media by taking the limit as the losses (the imaginary part of ε) go to zero. For any nonzero loss, the fields decay exponentially with distance and the surface integral vanishes, regardless of whether the medium is homogeneous. Since the left-hand side of the Lorentz reciprocity theorem vanishes for integration over all space with any non-zero losses, it must also vanish in the limit as the losses go to zero. (Note that we implicitly assumed the standard boundary condition of zero incoming waves from infinity, because otherwise even an infinitesimal loss would eliminate the incoming waves and the limit would not give the lossless solution.)
Reciprocity and the Green's function
The inverse of the operator , i.e. in
, i.e. in  (which requires a specification of the boundary conditions at infinity in a lossless system), has the same symmetry as
(which requires a specification of the boundary conditions at infinity in a lossless system), has the same symmetry as  and is essentially a Green's function
and is essentially a Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. So, another perspective on Lorentz reciprocity is that it reflects the fact that convolution with the electromagnetic Green's function is a complex-symmetric (or anti-Hermitian, below) linear operation under the appropriate conditions on ε and μ. More specifically, the Green's function can be written as
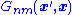 giving the n-th component of
giving the n-th component of  at
at 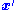 from a point dipole current in the m-th direction at
from a point dipole current in the m-th direction at  (essentially,
(essentially,  gives the matrix elements of
gives the matrix elements of 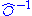 ), and Rayleigh-Carson reciprocity is equivalent to the statement that
), and Rayleigh-Carson reciprocity is equivalent to the statement that 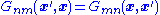 . Unlike
. Unlike  , it is not generally possible to give an explicit formula for the Green's function (except in special cases such as homogeneous media), but it is routinely computed by numerical methods.
, it is not generally possible to give an explicit formula for the Green's function (except in special cases such as homogeneous media), but it is routinely computed by numerical methods.Lossless magneto-optic materials
One case in which ε is not a symmetric matrix is for magneto-optic materials, in which case the usual statement of Lorentz reciprocity does not hold (see below for a generalization, however). If we allow magneto-optic materials, but restrict ourselves to the situation where material absorption is negligible, then ε and μ are in general 3×3 complex Hermitian matrices. In this case the operator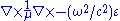 is Hermitian under the conjugated inner product
is Hermitian under the conjugated inner product 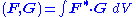 , and a variant of the reciprocity theorem still holds:
, and a variant of the reciprocity theorem still holds: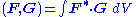
where the sign changes come from the
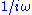 in the equation above, which makes the operator
in the equation above, which makes the operator  anti-Hermitian (neglecting surface terms). For the special case of
anti-Hermitian (neglecting surface terms). For the special case of  , this gives a re-statement of conservation of energy
, this gives a re-statement of conservation of energyConservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
or Poynting's theorem
Poynting's theorem
Poynting's theorem is a statement due to British physicist John Henry Poynting about the conservation of energy for the electromagnetic field. Poynting's theorem takes into account the case when the electric and magnetic fields are coupled – static or stationary electric and magnetic fields are not...
(since here we have assumed lossless materials, unlike above): the time-average rate of work done by the current (given by the real part of
 ) is equal to the time-average outward flux of power (the integral of the Poynting vector
) is equal to the time-average outward flux of power (the integral of the Poynting vectorPoynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
). By the same token, however, the surface terms do not in general vanish if one integrates over all space for this reciprocity variant, so a Rayleigh-Carson form does not hold without additional assumptions.
The fact that magneto-optic materials break Rayleigh-Carson reciprocity is the key to devices such as Faraday isolators and circulator
Circulator
A circulator is a passive non-reciprocal three- or four-port device, in which microwave or radio frequency power entering any port is transmitted to the next port in rotation...
s. A current on one side of a Faraday isolator produces a field on the other side but not vice-versa.
Generalization to non-symmetric materials
For a combination of lossy and magneto-optic materials, and in general when the ε and μ tensors are neither symmetric nor Hermitian matrices, one can still obtain a generalized version of Lorentz reciprocity by considering and
and 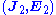 to exist in different systems.
to exist in different systems.In particular, if
 satisfy Maxwell's equations at ω for a system with materials
satisfy Maxwell's equations at ω for a system with materials 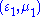 , and
, and 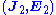 satisfy Maxwell's equations at ω for a system with materials
satisfy Maxwell's equations at ω for a system with materials 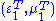 , where T denotes the transpose
, where T denotes the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
, then the equation of Lorentz reciprocity holds.
Exceptions to reciprocity
For nonlinear mediaNonlinear optics
Nonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
, no reciprocity theorem generally holds. Reciprocity also does not generally apply for time-varying ("active") media; for example, when ε is modulated in time by some external process. (In both of these cases, the frequency ω is not generally a conserved quantity.)
Feld-Tai reciprocity
A closely related reciprocity theorem was articulated independently by Y. A. Feld and C. T. Tai in 1992 and is known as Feld-Tai reciprocity or the Feld-Tai lemma. It relates two time-harmonic localized current sources and the resulting magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s:
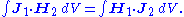
However, the Feld-Tai lemma is only valid under much more restrictive conditions than Lorentz reciprocity. It generally requires time-invariant linear media with an isotropic homogeneous impedance
Electrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
, i.e. a constant scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
μ/ε ratio, with the possible exception of regions of perfectly conducting material.
More precisely, Feld-Tai reciprocity requires the Hermitian (or rather, complex-symmetric) symmetry of the electromagnetic operators as above, but also relies on the assumption that the operator relating
 and
and  is a constant scalar multiple of the operator relating
is a constant scalar multiple of the operator relating  and
and 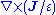 , which is true when ε is a constant scalar multiple of μ (the two operators generally differ by an interchange of ε and μ). As above, one can also construct a more general formulation for integrals over a finite volume.
, which is true when ε is a constant scalar multiple of μ (the two operators generally differ by an interchange of ε and μ). As above, one can also construct a more general formulation for integrals over a finite volume.Green's reciprocity
Whereas the above reciprocity theorems were for oscillating fields, Green's reciprocity is an analogous theorem for electrostatics with a fixed distribution of electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
(Panofsky and Phillips, 1962).
In particular, let
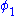 denote the electric potential resulting from a total charge density
denote the electric potential resulting from a total charge density 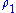 . The electric potential satisfies Poisson's equation
. The electric potential satisfies Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
,
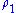 , where
, where 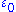 is the vacuum permittivity. Similarly, let
is the vacuum permittivity. Similarly, let  denote the electric potential resulting from a total charge density
denote the electric potential resulting from a total charge density 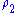 , satisfying
, satisfying 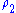 . In both cases, we assume that the charge distributions are localized, so that the potentials can be chosen to go to zero at infinity. Then, Green's reciprocity theorem states that, for integrals over all space:
. In both cases, we assume that the charge distributions are localized, so that the potentials can be chosen to go to zero at infinity. Then, Green's reciprocity theorem states that, for integrals over all space: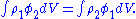
This theorem is easily proven from Green's second identity. Equivalently, it is the statement that
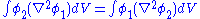 , i.e. that
, i.e. that  is a Hermitian operator (as follows by integrating by parts twice).
is a Hermitian operator (as follows by integrating by parts twice).


