
Salem number
Encyclopedia
In mathematics
, a real
algebraic integer
α > 1 is a Salem number if all its conjugate roots have absolute value
no greater than 1, and at least one has absolute value
exactly 1. Salem numbers are of interest in Diophantine approximation
and harmonic analysis
. They are named after Raphaël Salem
.
1, the minimal polynomial
for a Salem number must be reciprocal. This implies that 1/|α| is also a root, and that all other roots have absolute value
exactly one. As a consequence α must be a unit
in the ring of algebraic integer
s, being of norm
1.
)
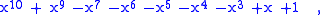
which is about 1.17628.
The smallest Pisot–Vijayaraghavan number is the unique real root of the cubic polynomial
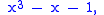
known as the plastic number
and approximately equal to 1.324718. This polynomial can be used to generate a family of Salem numbers including the smallest one found so far (x ≈ 1.176280) by Lehmer. The general approach is to take the minimal polynomial P(x) of a Pisot–Vijayaraghavan number and its reciprocal polynomial, P*(x), to form the equation,

for integral n above a bound. Subtracting one side from the other, factoring, and disregarding trivial factors yields the minimal polynomial of certain Salem numbers. For example, using the negative case of the above,

then for n = 8, this factors as,
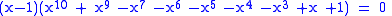
where the decic has the root x ≈ 1.176280 which is the aforementioned smallest known Salem number given by Lehmer. Using higher n will yield a family with a root approaching the plastic number
. This can be better understood by taking nth roots of both sides,
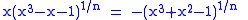
so as n goes higher, x will approach the solution of x3 − x − 1 = 0 (as well as the reciprocal for even degree equations). If the positive case is used, then x approaches the plastic number from the opposite direction. Using the minimal polynomial of the next smallest Pisot–Vijayaraghavan number gives,

which for n = 7 factors as,
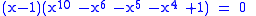
a decic not generated in the previous and has the root x = 1.216391... which is the 5th smallest known Salem number. As n → infinity, this family in turn tends towards the larger real root of x4 − x3 − 1 = 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
α > 1 is a Salem number if all its conjugate roots have absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
no greater than 1, and at least one has absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
exactly 1. Salem numbers are of interest in Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. They are named after Raphaël Salem
Raphaël Salem
Raphaël Salem, was a Greek-Sephardic mathematician after whom are named the Salem numbers and whose widow founded the Salem Prize.-Biography:...
.
Properties
Because it has a root of absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1, the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
for a Salem number must be reciprocal. This implies that 1/|α| is also a root, and that all other roots have absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
exactly one. As a consequence α must be a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in the ring of algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s, being of norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
1.
Relation with Pisot–Vijayaraghavan numbers
The smallest known Salem number is the largest real root of Lehmer's polynomial (named after Derrick Henry LehmerDerrick Henry Lehmer
Derrick Henry "Dick" Lehmer was an American mathematician who refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer test for Mersenne primes...
)
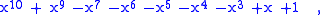
which is about 1.17628.
The smallest Pisot–Vijayaraghavan number is the unique real root of the cubic polynomial
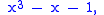
known as the plastic number
Plastic number
In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, ....
and approximately equal to 1.324718. This polynomial can be used to generate a family of Salem numbers including the smallest one found so far (x ≈ 1.176280) by Lehmer. The general approach is to take the minimal polynomial P(x) of a Pisot–Vijayaraghavan number and its reciprocal polynomial, P*(x), to form the equation,

for integral n above a bound. Subtracting one side from the other, factoring, and disregarding trivial factors yields the minimal polynomial of certain Salem numbers. For example, using the negative case of the above,

then for n = 8, this factors as,
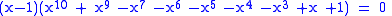
where the decic has the root x ≈ 1.176280 which is the aforementioned smallest known Salem number given by Lehmer. Using higher n will yield a family with a root approaching the plastic number
Plastic number
In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, ....
. This can be better understood by taking nth roots of both sides,
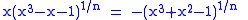
so as n goes higher, x will approach the solution of x3 − x − 1 = 0 (as well as the reciprocal for even degree equations). If the positive case is used, then x approaches the plastic number from the opposite direction. Using the minimal polynomial of the next smallest Pisot–Vijayaraghavan number gives,

which for n = 7 factors as,
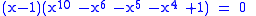
a decic not generated in the previous and has the root x = 1.216391... which is the 5th smallest known Salem number. As n → infinity, this family in turn tends towards the larger real root of x4 − x3 − 1 = 0.

