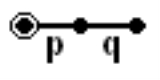
Schläfli symbol
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Schläfli symbol is a notation of the form {p,q,r,...} that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century mathematician Ludwig Schläfli
Ludwig Schläfli
Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
who made important contributions in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and other areas.
Description
The Schläfli symbol is a recursiveRecursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
description, starting with a p-sided regular polygon as {p}. For example, {3} is an equilateral triangle, {4} is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
and so on.
A regular polyhedron which has q regular p-gon faces around each vertex is represented by {p,q}. For example, the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
has 3 squares around each vertex and is represented by {4,3}.
A regular 4-polytope with r {p,q} regular polyhedral cells around each edge is represented by {p,q,r}, and so on.
Regular polytopes can have star polygon elements, like the pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
, with symbol {5/2}, represented by the vertices of a pentagon but connected alternately.
A facet
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
of a regular polytope {p,q,r,...,y,z} is {p,q,r,...,y}.
A regular polytope has a regular vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
. The vertex figure of a regular polytope {p,q,r,...} is {q,r,...}.
The Schläfli symbol can represent a finite convex polyhedron, an infinite tessellation of Euclidean space, or an infinite tessellation of hyperbolic space, depending on the angle defect of the construction. A positive angle defect allows the vertex figure to fold into a higher dimension and loops back into itself as a polytope. A zero angle defect will tessellate space of the same dimension as the facets. A negative angle defect can't exist in ordinary space, but can be constructed in hyperbolic space.
Usually a vertex figure is assumed to be a finite polytope, but can sometimes be considered a tessellation itself.
A regular polytope also has a dual polytope, represented by the Schläfli symbol elements in reverse order. A self-dual regular polytope will have a symmetric Schläfli symbol.
Symmetry groups
A Schläfli symbol is closely related to reflection symmetry groups, also called Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s, given with the same indices, but square brackets instead [p,q,r,...]. Such groups are often named by the regular polytopes they generate. For example [3,3] is the Coxeter group for Tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
, and [3,4] is octahedral symmetry
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
, and [3,5] is icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
.
Regular polygons (plane)
The Schläfli symbol of a regular polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with n edges is {n}.
For example, a regular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
is represented by {5}.
See the convex regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
and nonconvex star polygon.
For example, {5/2} is the pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
.
Regular polyhedra (3-space)
The Schläfli symbol of a regular polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
is {p,q} if its faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
are p-gons, and each vertex is surrounded by q faces (the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a q-gon).
For example {5,3} is the regular dodecahedron. It has pentagonal faces, and 3 pentagons around each vertex.
See the 5 convex Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, the 4 nonconvex Kepler-Poinsot polyhedra.
Schläfli symbols may also be defined for regular tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s of Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
or hyperbolic
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
space in a similar way.
For example, the hexagonal tiling is represented by {6,3}.
Regular polychora (4-space)
The Schläfli symbol of a regular polychoronPolychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
is of the form {p,q,r}. Its (two-dimensional) faces are regular p-gons ({p}), the cells are regular polyhedra of type {p,q}, the vertex figures are regular polyhedra of type {q,r}, and the edge figures are regular r-gons (type {r}).
See the six convex regular
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
and 10 nonconvex polychora.
For example, the 120-cell is represented by {5,3,3}. It is made of dodecahedron cells {5,3}, and has 3 cells around each edge.
There is also one regular tessellation of Euclidean 3-space: the cubic honeycomb
Cubic honeycomb
The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
, with a Schläfli symbol of {4,3,4}, made of cubic cells, and 4 cubes around each edge.
There are also 4 regular hyperbolic tessellations including {5,3,4}, the Hyperbolic small dodecahedral honeycomb
Hyperbolic small dodecahedral honeycomb
In the geometry of hyperbolic 3-space, the order-4 dodecahedral honeycomb is one of four regular space-filling tessellation . Four dodecahedra exist around each edge, and 8 dodecahedra around each vertex in an octahedral arrangement. Its vertices are constructed from 3 orthogonal axes...
, which fills space with dodecahedron cells.
Higher dimensions
For higher dimensional polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s, the Schläfli symbol is defined recursively as {p1, p2, ..., pn − 1} if the facet
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
s have Schläfli symbol {p1,p2, ..., pn − 2} and the
vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s have Schläfli symbol {p2,p3, ..., pn − 1}.
Notice that a vertex figure of a facet of a polytope and a facet of a vertex figure of the same polytope are the same: {p2,p3, ..., pn − 2}.
There are only 3 regular polytopes in 5 dimensions and above: the simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, {3,3,3,...,3}; the cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
, {3,3, ... ,3,4}; and the hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
, {4,3,3,...,3}. There are no non-convex regular polytopes above 4 dimensions.
Dual polytopes
If a polytope of dimension ≥ 2 has Schläfli symbol {p1,p2, ..., pn − 1} then its dualDual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
has Schläfli symbol {pn − 1, ..., p2,p1}.
If the sequence is palindromic, i.e. the same forwards and backwards, the polytope is self-dual. Every regular polytope in 2 dimensions (polygon) is self-dual.
Uniform prismatic polytopes
Uniform prismatic polytopes can be defined and named as a Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of lower dimensional regular polytopes:
- A p-gonal prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
, with vertex figure p.4.4 as . The symbol { } means a unit line.
. The symbol { } means a unit line. - A uniform {p,q}-hedral prism as
 .
. - A uniform p-q duoprismDuoprismIn geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
as .
.
Extension of Schläfli symbols
Coxeter expanded his usage of the Schläfli symbol to quasiregular polyhedra by adding a vertical dimension to the symbol. It was a starting point toward the more general Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
.
| Form | Extended Schläfli symbol | t-notation | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|---|---|---|---|
| Regular |  |
t0{p,q} | |
| Quasiregular |  |
t1{p,q} | |
| Regular dual |  |
t2{p,q} |
And for rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
4-polytopes:
| Form | Extended Schläfli symbol | t-notation | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|---|---|---|---|
| Regular |  |
t0{p,q,r} | |
| Rectified |  |
t1{p,q,r} | |
| Rectified dual |  |
t2{p,q,r} | |
| Regular dual |  |
t3{p,q,r} |

