
Signature matrix
Encyclopedia
In mathematics
, a signature matrix is a diagonal matrix
whose diagonal elements are plus or minus 1, that is, any matrix of the form:
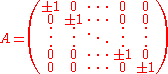
Any such matrix is its own inverse, hence is an involutary matrix. It is consequently a square root
of the identity matrix
. Note however that not all square roots of the identity are signature matrices.
Noting that signature matrices are both symmetric and involutary, they are thus orthogonal
. Consequently, any linear transformation corresponding to a signature matrix constitutes an isometry
.
Geometrically, signature matrices represent a reflection
in each of the axes corresponding to the negated rows or columns.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a signature matrix is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
whose diagonal elements are plus or minus 1, that is, any matrix of the form:
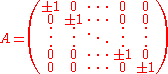
Any such matrix is its own inverse, hence is an involutary matrix. It is consequently a square root
Square root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
of the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Note however that not all square roots of the identity are signature matrices.
Noting that signature matrices are both symmetric and involutary, they are thus orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. Consequently, any linear transformation corresponding to a signature matrix constitutes an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
.
Geometrically, signature matrices represent a reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
in each of the axes corresponding to the negated rows or columns.

