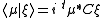Spinors in three dimensions
Encyclopedia
In mathematics
, the spinor
concept as specialised to three dimensions can be treated by means of the traditional notions of dot product
and cross product
. This is part of the detailed algebraic discussion of the rotation group SO(3).
, by means of quaternions. In detail, given a vector x = (x1, x2, x3) of real (or complex) numbers, one can associate the matrix of complex numbers: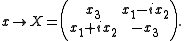
Matrices of this form have the following properties, which relate them intrinsically to the geometry of 3-space:
Having effectively encoded all of the rotational linear geometry of 3-space into a set of complex 2×2 matrices, it is natural to ask what role, if any, the 2×1 matrices (i.e., the column vectors) play. Provisionally, a spinor is a column vector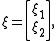
with complex entries ξ1 and ξ2.
The space of spinors is evidently acted upon by complex 2×2 matrices. Furthermore, the product of two reflections in a given pair of unit vectors defines a 2×2 matrix whose action on euclidean vectors is a rotation, so there is an action of rotations on spinors. However, there is one important caveat: the factorization of a rotation is not unique. Clearly, if X → RXR-1 is a representation of a rotation, then replacing R by -R will yield the same rotation. In fact, one can easily show that this is the only ambiguity which arises. Thus the action of a rotation on a spinor is always double-valued.
s in 3-space without using the quaternionic construction. To motivate this introduction of spinors, suppose that X is a matrix representing a vector x in complex 3-space. Suppose further that x is isotropic: i.e.,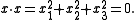
Then, from the properties of these matrices, X2=0. Any such matrix admits a factorization as an outer product
This factorization yields an overdetermined system
of equations in the coordinates of the vector x: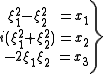
(1)
subject to the constraint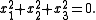
(2)
This system admits the solutions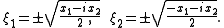
(3)
Either choice of sign solves the system (1). Thus a spinor may be viewed as an isotropic vector, along with a choice of sign. Note that because of the logarithmic branching, it is impossible to choose a sign consistently so that (3) varies continuously along a full rotation among the coordinates x. In spite of this ambiguity of the representation of a rotation on a spinor, the rotations do act unambiguously by a fractional linear transformation on the ratio ξ1:ξ2 since one choice of sign in the solution (3) forces the choice of the second sign. In particular, the space of spinors is a projective representation
of the orthogonal group.
As a consequence of this point of view, spinors may be regarded as a kind of "square root" of isotropic vectors. Specifically, introducing the matrix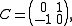
the system (1) is equivalent to solving X = 2 ξ tξ C for the undetermined spinor ξ.
A fortiori, if the roles of ξ and x are now reversed, the form Q(ξ) = x defines, for each spinor ξ, a vector x quadratically in the components of ξ. If this quadratic form is polarized
, it determines a bilinear vector-valued form on spinors Q(μ,ξ). This bilinear form then transform tensorially under a reflection or a rotation.
With this convention, real vectors correspond to hermitian matrices. Furthermore, real rotations preserving the form (4) correspond (in the double-valued sense) to unitary matrices of determinant one. In modern terms, this presents the special unitary group
SU(2) as a double cover of SO(3). As a consequence, the spinor hermitian product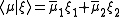
(5)
is preserved by all rotations, and therefore is canonical.
If, however, the signature of the inner product on 3-space is indefinite (i.e., non-degenerate, but also not positive definite), then the foregoing analysis must be adjusted to reflect this. Suppose then that the length form on 3-space is given by:
Then the construction of spinors of the preceding sections proceeds, but with x2 replacing i x2 in all the formulas. With this new convention, the matrix associated to a real vector (x1,x2,x3) is itself real: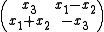
.
The form (5) is no longer invariant under a real rotation (or reversal), since the group stabilizing (4') is now a Lorentz group
O(2,1). Instead, the antihermitian form
defines the appropriate notion of inner product for spinors in this metric signature. This form is invariant under transformations in the connected component of the identity of O(2,1).
In either case, the quartic form
is fully invariant under O(3) (or O(2,1), respectively), where Q is the vector-valued bilinear form described in the previous section. The fact that this is a quartic invariant, rather than quadratic, has an important consequence. If one confines attention to the group of special orthogonal transformations, then it is possible unambiguously to take the square root of this form and obtain an identification of spinors with their duals. In the language of representation theory, this implies that there is only one irreducible spin representation of SO(3) (or SO(2,1)) up to isomorphism. If, however, reversals (e.g., reflections in a plane) are also allowed, then it is no longer possible to identify spinors with their duals owing to a change of sign on the application of a reflection. Thus there are two irreducible spin representations of O(3) (or O(2,1)), sometimes called the pin representations.
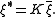
The particular form of the inner product on vectors (e.g., (4) or (4')) determines a reality structure (up to a factor of -1) by requiring
, whenever X is a matrix associated to a real vector.
Thus K = i C is the reality structure in euclidean signature (4), and K = Id is that for signature (4'). With a reality structure in hand, one has the following results:
encounters are the 2x1 spinors used in Pauli's theory of electron spin.
The Pauli matrices
are a vector of three 2x2 matrices
that are used as spin
operators
.
Given a unit vector in 3 dimensions, for example (a,b,c), one takes a
dot product
with the Pauli spin matrices to obtain a spin matrix for
spin in the direction of the unit vector.
The eigenvectors of that spin matrix are the spinors for
spin-1/2 oriented in the direction given by the vector.
Example: u = (0.8, -0.6, 0) is a unit vector. Dotting this with the Pauli
spin matrices gives the matrix:
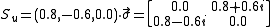
The eigenvectors may be found by the usual methods of
linear algebra
, but a convenient trick
is to note that the Pauli spin matrices are square
roots of unity, that is, the square
of the above matrix is the identity matrix
.
Thus a (matrix) solution to the eigenvector problem with eigenvalues of
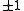is simply
. That is,
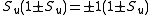
One can then choose either of the columns of the eigenvector
matrix as the vector solution, provided that the column chosen
is not zero. Taking the first column of the above,
eigenvector solutions for the two eigenvalues are:
The trick used to find the eigenvectors is related to the concept of
ideals
, that is, the matrix eigenvectors
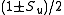are projection operators
or idempotents and therefore each generates an
ideal
in the Pauli algebra. The same trick
works in any Clifford algebra
, in particular
the Dirac algebra that are discussed below. These projection
operators are also seen in density matrix
theory
where they are examples of pure density matrices.
More generally, the projection operator for spin in the (a,b,c) direction
is given by
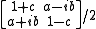
and any non zero column can be taken as the projection operator. While the
two columns appear different, one can use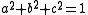
to show that they are multiples (possibly zero) of the same spinor.
, the property of spin plays a major role. In addition to their other properties all particles possess a non-classical property, i.e., which has no correspondence at all in conventional physics, namely the spin
, which is a kind of intrinsic angular momentum. In the position representation, instead of a wavefunction without spin,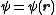
, one has with spin: 
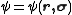, where 
belongs to the following discrete set of values: 
.
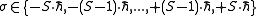The operator of the total angular momentum,
, of a particle corresponds to the sum of the orbital angular momentum (i.e., there only integers are allowed) and the intrinsic part, the spin. One distinguishes boson
s (S = 0 or ±1 or ±2 or ...) and fermion
s (S = ±1/2 or ±3/2 or ±5/2 or ...)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
concept as specialised to three dimensions can be treated by means of the traditional notions of dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. This is part of the detailed algebraic discussion of the rotation group SO(3).
Formulation
This algebra admits a convenient description, due to William Rowan HamiltonWilliam Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
, by means of quaternions. In detail, given a vector x = (x1, x2, x3) of real (or complex) numbers, one can associate the matrix of complex numbers:
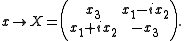
Matrices of this form have the following properties, which relate them intrinsically to the geometry of 3-space:
- det X = - (length x)2.
- X2 = (length x)2I, where I is the identity matrix.
-
-
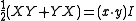
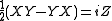where Z is the matrix associated to the cross product z = x × y. - If u is a unit vector, then -UXU is the matrix associated to the vector obtained from x by reflection in the plane orthogonal to u.
- It is an elementary fact from linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
that any rotation in 3-space factors as a composition of two reflections. (Similarly, any orientation reversing orthogonal transformation is either a reflection or the product of three reflections.) Thus if R is a rotation, decomposing as the reflection in the plane perpendicular to a unit vector u1 followed by the plane perpendicular to u2, then the matrix U2U1XU1U2 represents the rotation of the vector x through R.
Having effectively encoded all of the rotational linear geometry of 3-space into a set of complex 2×2 matrices, it is natural to ask what role, if any, the 2×1 matrices (i.e., the column vectors) play. Provisionally, a spinor is a column vector
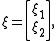with complex entries ξ1 and ξ2.The space of spinors is evidently acted upon by complex 2×2 matrices. Furthermore, the product of two reflections in a given pair of unit vectors defines a 2×2 matrix whose action on euclidean vectors is a rotation, so there is an action of rotations on spinors. However, there is one important caveat: the factorization of a rotation is not unique. Clearly, if X → RXR-1 is a representation of a rotation, then replacing R by -R will yield the same rotation. In fact, one can easily show that this is the only ambiguity which arises. Thus the action of a rotation on a spinor is always double-valued.
Isotropic vectors
Spinors can be constructed directly from isotropic vectorIsotropic line
An isotropic line or null line is a line in the complex projective plane with slope i or -i.-Equation:All isotropic lines have equations of the following form:y = ix + az or y = -ix + az,...
s in 3-space without using the quaternionic construction. To motivate this introduction of spinors, suppose that X is a matrix representing a vector x in complex 3-space. Suppose further that x is isotropic: i.e.,
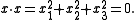
Then, from the properties of these matrices, X2=0. Any such matrix admits a factorization as an outer product
This factorization yields an overdetermined system
Overdetermined system
In mathematics, a system of linear equations is considered overdetermined if there are more equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
of equations in the coordinates of the vector x:
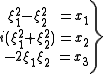(1)subject to the constraint
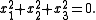(2)This system admits the solutions
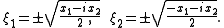(3)Either choice of sign solves the system (1). Thus a spinor may be viewed as an isotropic vector, along with a choice of sign. Note that because of the logarithmic branching, it is impossible to choose a sign consistently so that (3) varies continuously along a full rotation among the coordinates x. In spite of this ambiguity of the representation of a rotation on a spinor, the rotations do act unambiguously by a fractional linear transformation on the ratio ξ1:ξ2 since one choice of sign in the solution (3) forces the choice of the second sign. In particular, the space of spinors is a projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
of the orthogonal group.
As a consequence of this point of view, spinors may be regarded as a kind of "square root" of isotropic vectors. Specifically, introducing the matrix
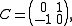
the system (1) is equivalent to solving X = 2 ξ tξ C for the undetermined spinor ξ.
A fortiori, if the roles of ξ and x are now reversed, the form Q(ξ) = x defines, for each spinor ξ, a vector x quadratically in the components of ξ. If this quadratic form is polarized
Polarization of an algebraic form
In mathematics, in particular in algebra, polarization is a technique for expressing a homogeneous polynomial in a simpler fashion by adjoining more variables...
, it determines a bilinear vector-valued form on spinors Q(μ,ξ). This bilinear form then transform tensorially under a reflection or a rotation.
Reality
The above considerations apply equally well whether the original euclidean space under consideration is real or complex. When the space is real, however, spinors possess some additional structure which in turn facilitates a complete description of the representation of the rotation group. Suppose, for simplicity, that the inner product on 3-space has positive-definite signature:- length(x)2 = x12 + x22 + x32 (4).
With this convention, real vectors correspond to hermitian matrices. Furthermore, real rotations preserving the form (4) correspond (in the double-valued sense) to unitary matrices of determinant one. In modern terms, this presents the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
SU(2) as a double cover of SO(3). As a consequence, the spinor hermitian product
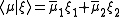(5)is preserved by all rotations, and therefore is canonical.
If, however, the signature of the inner product on 3-space is indefinite (i.e., non-degenerate, but also not positive definite), then the foregoing analysis must be adjusted to reflect this. Suppose then that the length form on 3-space is given by:
- length(x)2 = x12 - x22 + x32 (4').
Then the construction of spinors of the preceding sections proceeds, but with x2 replacing i x2 in all the formulas. With this new convention, the matrix associated to a real vector (x1,x2,x3) is itself real:
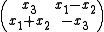.The form (5) is no longer invariant under a real rotation (or reversal), since the group stabilizing (4') is now a Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
O(2,1). Instead, the antihermitian form
defines the appropriate notion of inner product for spinors in this metric signature. This form is invariant under transformations in the connected component of the identity of O(2,1).
In either case, the quartic form
is fully invariant under O(3) (or O(2,1), respectively), where Q is the vector-valued bilinear form described in the previous section. The fact that this is a quartic invariant, rather than quadratic, has an important consequence. If one confines attention to the group of special orthogonal transformations, then it is possible unambiguously to take the square root of this form and obtain an identification of spinors with their duals. In the language of representation theory, this implies that there is only one irreducible spin representation of SO(3) (or SO(2,1)) up to isomorphism. If, however, reversals (e.g., reflections in a plane) are also allowed, then it is no longer possible to identify spinors with their duals owing to a change of sign on the application of a reflection. Thus there are two irreducible spin representations of O(3) (or O(2,1)), sometimes called the pin representations.
Reality structures
The differences between these two signatures can be codified by the notion of a reality structure on the space of spinors. Informally, this is a prescription for taking a complex conjugate of a spinor, but in such a way that this may not correspond to the usual conjugate per the components of a spinor. Specifically, a reality structure is specified by a hermitian 2 × 2 matrix K whose product with itself is the identity matrix: K2 = Id. The conjugate of a spinor with respect to a reality structure K is defined by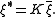The particular form of the inner product on vectors (e.g., (4) or (4')) determines a reality structure (up to a factor of -1) by requiring
, whenever X is a matrix associated to a real vector.Thus K = i C is the reality structure in euclidean signature (4), and K = Id is that for signature (4'). With a reality structure in hand, one has the following results:
- X is the matrix associated to a real vector if, and only if,
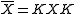. - If μ and ξ is a spinor, then the inner product
-
- determines a hermitian form which is invariant under proper orthogonal transformations.
Spinors of the Pauli spin matrices
Often, the first example of spinors that a student of physicsencounters are the 2x1 spinors used in Pauli's theory of electron spin.
The Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
are a vector of three 2x2 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that are used as spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
operators
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
.
Given a unit vector in 3 dimensions, for example (a,b,c), one takes a
dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
with the Pauli spin matrices to obtain a spin matrix for
spin in the direction of the unit vector.
The eigenvectors of that spin matrix are the spinors for
spin-1/2 oriented in the direction given by the vector.
Example: u = (0.8, -0.6, 0) is a unit vector. Dotting this with the Pauli
spin matrices gives the matrix:
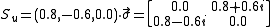
The eigenvectors may be found by the usual methods of
linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, but a convenient trick
is to note that the Pauli spin matrices are square
roots of unity, that is, the square
of the above matrix is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
Thus a (matrix) solution to the eigenvector problem with eigenvalues of
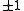is simply. That is,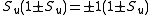One can then choose either of the columns of the eigenvector
matrix as the vector solution, provided that the column chosen
is not zero. Taking the first column of the above,
eigenvector solutions for the two eigenvalues are:
The trick used to find the eigenvectors is related to the concept of
ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, that is, the matrix eigenvectors
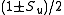are projection operatorsor idempotents and therefore each generates an
ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in the Pauli algebra. The same trick
works in any Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
, in particular
the Dirac algebra that are discussed below. These projection
operators are also seen in density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
theory
where they are examples of pure density matrices.
More generally, the projection operator for spin in the (a,b,c) direction
is given by
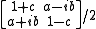
and any non zero column can be taken as the projection operator. While the
two columns appear different, one can use
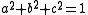
to show that they are multiples (possibly zero) of the same spinor.
General remarks
In atomic physics and quantum mechanicsMathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
, the property of spin plays a major role. In addition to their other properties all particles possess a non-classical property, i.e., which has no correspondence at all in conventional physics, namely the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, which is a kind of intrinsic angular momentum. In the position representation, instead of a wavefunction without spin,
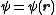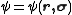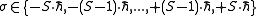, one has with spin: , where belongs to the following discrete set of values: .The operator of the total angular momentum,
, of a particle corresponds to the sum of the orbital angular momentum (i.e., there only integers are allowed) and the intrinsic part, the spin. One distinguishes bosonBoson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s (S = 0 or ±1 or ±2 or ...) and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s (S = ±1/2 or ±3/2 or ±5/2 or ...)