Stars and bars (probability)
Encyclopedia
In the context of combinatorial mathematics, stars and bars is a graphical aid for deriving certain combinatorial theorems. It was popularized by William Feller
in his classic book on probability.
s of positive integers whose sum is k is given by the binomial coefficient
.
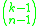s n and k, the number of distinct n-tuple
s of non-negative integers whose sum is k is given by the binomial coefficient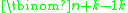
, or equivalently by the multiset number 
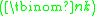which counts the multiset
s of cardinality k, with elements taken from a set of n elements (for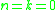
both these numbers are defined to be 1).
where the stars for the first bin will be taken from the left, followed by the stars for the second bin, and so forth. Thus the configuration will be determined once one knows what is the first star going to the second bin, and the first star going to the third bin, and so on. One can indicate this by placing n − 1 separating bars at some places between two stars; since no bin is allowed to be empty, there can be at most one bar between a given pair of stars:
Thus one views the k stars as fixed objects defining k − 1 gaps, in each of which there may or not be one bar (bin partition). One has to choose n − 1 of them to actually contain a bar; therefore there are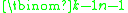
possible configurations (see combination
).
, one can apply theorem one to n + k objects, giving 
configurations with at least one object in each bin, and then remove one object from each bin to obtain a distribution of k objects into n bins, in which some bins may be empty. For example, placing 10 objects in 5 bins, allowing for bins to be empty, is equivalent to placing 15 objects in 5 bins and forcing something to be in each bin. An alternative way to arrive directly at the binomial coefficient: in a sequence of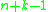 
symbols, one has to choose k of them to be stars and the remaining 
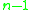to be bars (which can now be next to each other).
The case n = 0 (no bins at all) allows 0 configurations, unless k = 0 as well (no objects to place), in which there is one configuration (since an empty sum
is defined to be 0). In fact the binomial coefficient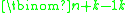
takes these values for n = 0 (since by convention 
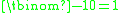(unlike 
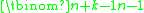, which by convention takes value 0 when 
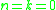, which is why the former expression is the one used in the statement of the theorem).
then ★|★★★||★ would represent the multiset {a, b, b, b, d} or the 4-tuple (1,3,0,1). The representation of any multiset for this example would use 5 stars (k) and 3 bars (n − 1).
Seven indistinguishable one dollar coins are to be distributed among Amber, Ben and Curtis so that each of them receives at least one dollar. Thus the stars and bars apply with n = 7 and k = 3; hence there are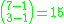
ways to distribute the coins.
William Feller
William Feller born Vilibald Srećko Feller , was a Croatian-American mathematician specializing in probability theory.-Early life and education:...
in his classic book on probability.
Theorem one
For any pair of positive integers n and k, the number of distinct n-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of positive integers whose sum is k is given by the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
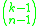.Theorem two
For any pair of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s n and k, the number of distinct n-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of non-negative integers whose sum is k is given by the binomial coefficient
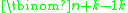, or equivalently by the multiset number 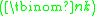which counts the multisetMultiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s of cardinality k, with elements taken from a set of n elements (for
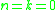both these numbers are defined to be 1).Theorem one
Suppose one has k objects (to be represented as stars; in the example below k = 7) to be placed into n bins (in the example n = 3), such that all bins contain at least one object; one distinguishes the bins (say they are numbered 1 to n) but one does not wish to distinguish the k stars (so configurations are only distinguished by the number of stars present in each bin; in fact a configuration is represented by a n-tuple of positive integers as in the statement of the theorem). Instead of starting to place stars into bins, one starts by placing the stars on a line:
|
where the stars for the first bin will be taken from the left, followed by the stars for the second bin, and so forth. Thus the configuration will be determined once one knows what is the first star going to the second bin, and the first star going to the third bin, and so on. One can indicate this by placing n − 1 separating bars at some places between two stars; since no bin is allowed to be empty, there can be at most one bar between a given pair of stars:
|
| Fig. 2: two bars give rise to three bins containing 4, 1, and 2 objects |
Thus one views the k stars as fixed objects defining k − 1 gaps, in each of which there may or not be one bar (bin partition). One has to choose n − 1 of them to actually contain a bar; therefore there are
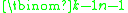possible configurations (see combinationCombination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
).
Theorem two
If, one can apply theorem one to n + k objects, giving configurations with at least one object in each bin, and then remove one object from each bin to obtain a distribution of k objects into n bins, in which some bins may be empty. For example, placing 10 objects in 5 bins, allowing for bins to be empty, is equivalent to placing 15 objects in 5 bins and forcing something to be in each bin. An alternative way to arrive directly at the binomial coefficient: in a sequence of 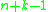symbols, one has to choose k of them to be stars and the remaining 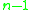to be bars (which can now be next to each other).The case n = 0 (no bins at all) allows 0 configurations, unless k = 0 as well (no objects to place), in which there is one configuration (since an empty sum
Empty sum
In mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero...
is defined to be 0). In fact the binomial coefficient
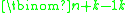takes these values for n = 0 (since by convention 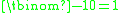(unlike 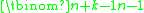, which by convention takes value 0 when 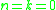, which is why the former expression is the one used in the statement of the theorem).Example
For example, if k = 5, n = 4, and a set of size n is {a, b, c, d},then ★|★★★||★ would represent the multiset {a, b, b, b, d} or the 4-tuple (1,3,0,1). The representation of any multiset for this example would use 5 stars (k) and 3 bars (n − 1).
Seven indistinguishable one dollar coins are to be distributed among Amber, Ben and Curtis so that each of them receives at least one dollar. Thus the stars and bars apply with n = 7 and k = 3; hence there are
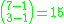ways to distribute the coins.