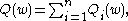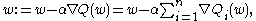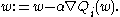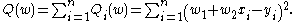Stochastic gradient descent
Encyclopedia
Stochastic gradient descent is an optimization
method
for minimizing an objective function that is written as a sum of differentiable functions.
estimation and machine learning
consider the problem of minimizing an objective function that has the form of a sum:
where the parameter
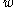is to be estimated
and where typically each summand function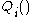
is associated with the 
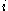-th observation
in the data set
(used for training).
In classical statistics, sum-minimization problems arise in least squares
and in maximum-likelihood estimation (for independent observations). The general class of estimators that arise as minimizers of sums are called M-estimator
s. However, in statistics, it has been long recognized that requiring even local minimization is too restrictive for some problems of maximum-likelihood estimation, as shown for example by Thomas Ferguson's example. Therefore, contemporary statisticial theorists often consider stationary points of the likelihood function
(or zeros of its derivative, the score function
, and other estimating equations
).
The sum-minimization problem also arises for empirical risk minimization
: In this case,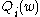
is the value of loss function
at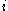
-th example, and 
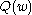is the empirical risk.
When used to minimize the above function, a standard (or "batch") gradient descent
method would perform the following iterations :
where
is a step size (sometimes called the learning rate in machine learning).
In many cases, the summand functions have a simple form that enables inexpensive evaluations of the sum-function and the sum gradient. For example, in statistics, one-parameter exponential families allow economical function-evaluations and gradient-evaluations.
However, in other cases, evaluating the sum-gradient may require expensive evaluations of the gradients from all summand functions. When the training set is enormous and no simple formulas exist, evaluating the sums of gradients becomes very expensive, because evaluating the gradient requires evaluating all the summand functions' gradients. To economize on the computational cost at every iteration, stochastic gradient descent samples
a subset of summand functions at every step.
In stochastic (or "on-line") gradient descent, the true gradient of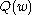 
is approximated by a gradient at a single example:
As the algorithm sweeps through the training set, it performs the above update for each training example. Several passes over the training set are made until the algorithm converges. Typical implementations may also randomly shuffle training examples at each pass and use an adaptive learning rate.
In pseudocode, stochastic gradient descent with shuffling of training set at each pass can be presented as follows:
There is a compromise between the two forms, which is often called "mini-batches", where the true gradient is approximated by a sum over a small number of training examples.
The convergence of stochastic gradient descent has been analyzed using the theories of convex minimization and of stochastic approximation
. Briefly, stochastic gradient methods need not converge to a global minimum unless the objective function is convex
--- or more generally unless the problem has convex lower level sets
and the function has the monotone property called "pseudoconvexity" in optimization theory, and finally the step-sizes are very small.
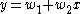to a training set of two-dimensional points 
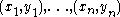using least squares
. The objective function to be minimized is:
The last line in the above pseudocode for this specific problem will become:
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for minimizing an objective function that is written as a sum of differentiable functions.
Background
Both statisticalStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
estimation and machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
consider the problem of minimizing an objective function that has the form of a sum:
where the parameter
Parametric statistics
Parametric statistics is a branch of statistics that assumes that the data has come from a type of probability distribution and makes inferences about the parameters of the distribution. Most well-known elementary statistical methods are parametric....
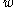is to be estimatedEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
and where typically each summand function
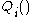is associated with the 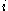-th observationObservation
Observation is either an activity of a living being, such as a human, consisting of receiving knowledge of the outside world through the senses, or the recording of data using scientific instruments. The term may also refer to any data collected during this activity...
in the data set
Data set
A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...
(used for training).
In classical statistics, sum-minimization problems arise in least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
and in maximum-likelihood estimation (for independent observations). The general class of estimators that arise as minimizers of sums are called M-estimator
M-estimator
In statistics, M-estimators are a broad class of estimators, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new...
s. However, in statistics, it has been long recognized that requiring even local minimization is too restrictive for some problems of maximum-likelihood estimation, as shown for example by Thomas Ferguson's example. Therefore, contemporary statisticial theorists often consider stationary points of the likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
(or zeros of its derivative, the score function
Score (statistics)
In statistics, the score, score function, efficient score or informant plays an important role in several aspects of inference...
, and other estimating equations
Estimating equations
In statistics, the method of estimating equations is a way of specifying how the parameters of a statistical model should be estimated. This can be thought of as a generalisation of many classical methods --- the method of moments, least squares, and maximum likelihood --- as well as some recent...
).
The sum-minimization problem also arises for empirical risk minimization
Empirical risk minimization
Empirical risk minimization is a principle in statistical learning theory which defines a family of learning algorithms and is used to give theoretical bounds on the performance of learning algorithms.- Background :...
: In this case,
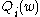is the value of loss functionLoss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
at
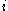-th example, and 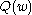is the empirical risk.When used to minimize the above function, a standard (or "batch") gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
method would perform the following iterations :
where
is a step size (sometimes called the learning rate in machine learning).In many cases, the summand functions have a simple form that enables inexpensive evaluations of the sum-function and the sum gradient. For example, in statistics, one-parameter exponential families allow economical function-evaluations and gradient-evaluations.
However, in other cases, evaluating the sum-gradient may require expensive evaluations of the gradients from all summand functions. When the training set is enormous and no simple formulas exist, evaluating the sums of gradients becomes very expensive, because evaluating the gradient requires evaluating all the summand functions' gradients. To economize on the computational cost at every iteration, stochastic gradient descent samples
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
a subset of summand functions at every step.
Iterative method
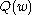is approximated by a gradient at a single example:
As the algorithm sweeps through the training set, it performs the above update for each training example. Several passes over the training set are made until the algorithm converges. Typical implementations may also randomly shuffle training examples at each pass and use an adaptive learning rate.
In pseudocode, stochastic gradient descent with shuffling of training set at each pass can be presented as follows:
There is a compromise between the two forms, which is often called "mini-batches", where the true gradient is approximated by a sum over a small number of training examples.
The convergence of stochastic gradient descent has been analyzed using the theories of convex minimization and of stochastic approximation
Stochastic approximation
Stochastic approximation methods are a family of iterative stochastic optimization algorithms that attempt to find zeroes or extrema of functions which cannot be computed directly, but only estimated via noisy observations....
. Briefly, stochastic gradient methods need not converge to a global minimum unless the objective function is convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
--- or more generally unless the problem has convex lower level sets
Quasiconvex function
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set...
and the function has the monotone property called "pseudoconvexity" in optimization theory, and finally the step-sizes are very small.
Example
Let's suppose we want to fit a straight line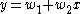 to a training set of two-dimensional points 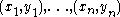using least squaresLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
. The objective function to be minimized is:
The last line in the above pseudocode for this specific problem will become:
-
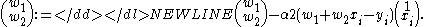
Applications
Some of the most popular stochastic gradient descent algorithms are the least mean squares (LMS)Least mean squares filterLeast mean squares algorithms are a class of adaptive filter used to mimic a desired filter by finding the filter coefficients that relate to producing the least mean squares of the error signal . It is a stochastic gradient descent method in that the filter is only adapted based on the error at...
adaptive filter and the backpropagationBackpropagationBackpropagation is a common method of teaching artificial neural networks how to perform a given task. Arthur E. Bryson and Yu-Chi Ho described it as a multi-stage dynamic system optimization method in 1969 . It wasn't until 1974 and later, when applied in the context of neural networks and...
algorithm.
External links
- sgd: an LGPL C++ library which uses stochastic gradient descent to fit SVMSupport vector machineA support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
and conditional random fieldConditional random fieldA conditional random field is a statistical modelling method often applied in pattern recognition.More specifically it is a type of discriminative undirected probabilistic graphical model. It is used to encode known relationships between observations and construct consistent interpretations...
models.
- sgd: an LGPL C++ library which uses stochastic gradient descent to fit SVM