Supersymmetry nonrenormalization theorems
Encyclopedia
In theoretical physics
a nonrenormalization theorem is a limitation on how a certain quantity in the classical description of a quantum field theory
may be modified by renormalization
in the full quantum theory. Renormalization theorems are common in theories with a sufficient amount of supersymmetry
, usually at least 4 supercharges.
Perhaps the first nonrenormalization theorem was introduced by Marcus T. Grisaru, Martin Rocek
and Warren Siegel
in their 1979 paper Improved methods for supergraphs.
. In this case the nonrenormalization theory is said to be a consequence of holomorphy.
The more supersymmetry a theory has, the more renormalization theorems apply. Therefore a renormalization theorem that is valid for a theory with
supersymmetries will also apply to any theory with more than 
supersymmetries.
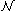counts the number of 4-component Majorana spinors of supercharges. Some examples of nonrenormalization theorems in 4-dimensional supersymmetric theories are:
In an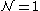
4D SUSY theory involving only chiral superfields, the superpotential
is immune from renormalization. With an arbitrary field content it is immune from renormalization in perturbation theory but may be renormalized by nonperturbative effects such as instantons.
In an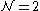
4D SUSY theory the moduli space
of the hypermultiplets
, called the Higgs branch, has a hyper-Kähler metric and is not renormalized. In the article Lagrangians of N=2 Supergravity - Matter Systems it was further shown that this metric is independent of the scalars
in the vector multiplets. They also proved that the metric of the Coulomb branch, which is a rigid special Kähler manifold
parametrized by the scalars in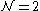
vector multiplets, is independent of the scalars in the hypermultiplets. Therefore the vacuum manifold is locally a product of a Columb and Higgs branch. The derivations of these statements appear in The Moduli Space of N=2 SUSY QCD and Duality in N=1 SUSY QCD.
In an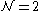
4D SUSY theory the superpotential is entirely determined by the matter content of the theory. Also there are no perturbative corrections to the β-function beyond one-loop, as was shown in 1983 in the article Superspace Or One Thousand and One Lessons in Supersymmetry by Sylvester James Gates
, Marcus Grisaru, Martin Rocek and Warren Siegel.
In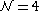
superYang-Mills the β-function is zero for all couplings, meaning that the theory is conformal
. This was demonstrated perturbatively by Martin Sohnius and Peter West
in the 1981 article Conformal Invariance in N=4 Supersymmetric Yang-Mills Theory under certain symmetry assumptions on the theory, and then with no assumptions by Stanley Mandelstam
in the 1983 article Light Cone Superspace and the Ultraviolet Finiteness of the N=4 Model. The full nonperturbative proof by Nathan Seiberg
appeared in the 1988 article Supersymmetry and Nonperturbative beta Functions.
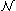counts the number of 2-component Majorana spinors of supercharges.
When
there is no holomorphicity and few exact results are known.
When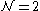
the superpotential cannot depend on the linear multiplets and in particular is independent of the Fayet-Iliopoulos terms (FI) and Majorana mass terms. On the other hand the central charge
is independent of the chiral multiplets, and so is a linear combination of the FI and Majorana mass terms. These two theorems were stated and proven in Aspects of N=2 Supersymmetric Gauge Theories in Three Dimensions.
When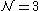
, unlike 
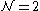, the R-symmetry
is the nonabelian group
SU(2) and so the representation
of each field is not renormalized. In a superconformal field theory the conformal dimension
of a chiral multiplet
is entirely determined by its R-charge, and so these conformal dimensions are not renormalized. Therefore matter fields have no wave function renormalization
in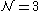
superconformal field theories, as was shown in On Mirror Symmetry in Three Dimensional Abelian Gauge Theories. These theories consist of vector multiplets and hypermultiplets. The hypermultiplet metric is hyperkähler and may not be lifted by quantum corrections, but its metric may be modified. No renormalizable
interaction between hyper and abelian vector multiplets is possible except for Chern-Simons terms
.
When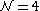
, unlike 
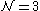the hypermultiplet metric may no longer be modified by quantum corrections.
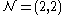linear sigma models, which are superrenormalizable abelian
gauge theories with matter in chiral supermultiplet
s, Edward Witten
has argued in Phases of N=2 theories in two-dimensions that the only divergent quantum correction is the logarithmic
one-loop correction to the FI term.
implies that it may only be renormalized at one-loop. In the 1994 article Nonrenormalization Theorem for Gauge Coupling in 2+1D the authors find the renormalization of the level can only be a finite shift, independent of the energy scale, and extended this result to topologically massive theories in which one includes a kinetic term
for the gluon
s. In Notes on Superconformal Chern-Simons-Matter Theories the authors then showed that this shift needs to occur at one loop, because any renormalization at higher loops would introduce inverse powers of the level, which are nonintegral and so would be in conflict with the quantization condition.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
a nonrenormalization theorem is a limitation on how a certain quantity in the classical description of a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
may be modified by renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
in the full quantum theory. Renormalization theorems are common in theories with a sufficient amount of supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
, usually at least 4 supercharges.
Perhaps the first nonrenormalization theorem was introduced by Marcus T. Grisaru, Martin Rocek
Martin Rocek
Martin Rocek is a professor of theoretical physics at the State University of New York at Stony Brook and a member of the C. N. Yang Institute for Theoretical Physics. He received A.B. and Ph.D. degrees from Harvard University in 1975 and 1979...
and Warren Siegel
Warren Siegel
Warren Siegel is a theoretical physicist specializing in supersymetric quantum field theory and string theory. He is a professor at the C. N. Yang Institute for Theoretical Physics at Stony Brook University in New York.-Background:...
in their 1979 paper Improved methods for supergraphs.
Nonrenormalization in supersymmetric theories and holomorphy
Nonrenormalization theorems in supersymmetric theories are often consequences of the fact that certain objects must have a holomorphic dependence on the quantum fields and coupling constantsCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
. In this case the nonrenormalization theory is said to be a consequence of holomorphy.
The more supersymmetry a theory has, the more renormalization theorems apply. Therefore a renormalization theorem that is valid for a theory with
supersymmetries will also apply to any theory with more than supersymmetries.Examples in 4-dimensional theories
In 4 dimensions the number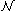 counts the number of 4-component Majorana spinors of supercharges. Some examples of nonrenormalization theorems in 4-dimensional supersymmetric theories are:In an
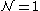4D SUSY theory involving only chiral superfields, the superpotentialSuperpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
is immune from renormalization. With an arbitrary field content it is immune from renormalization in perturbation theory but may be renormalized by nonperturbative effects such as instantons.
In an
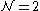4D SUSY theory the moduli spaceModuli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of the hypermultiplets
Supermultiplet
In theoretical physics, a supermultiplet is formally a group representation of a supersymmetry algebra. It consists of a collection of particles, called superpartners, corresponding to operators in a quantum field theory which in superspace are represented by superfields.Superfields were...
, called the Higgs branch, has a hyper-Kähler metric and is not renormalized. In the article Lagrangians of N=2 Supergravity - Matter Systems it was further shown that this metric is independent of the scalars
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
in the vector multiplets. They also proved that the metric of the Coulomb branch, which is a rigid special Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
parametrized by the scalars in
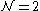vector multiplets, is independent of the scalars in the hypermultiplets. Therefore the vacuum manifold is locally a product of a Columb and Higgs branch. The derivations of these statements appear in The Moduli Space of N=2 SUSY QCD and Duality in N=1 SUSY QCD.In an
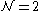4D SUSY theory the superpotential is entirely determined by the matter content of the theory. Also there are no perturbative corrections to the β-function beyond one-loop, as was shown in 1983 in the article Superspace Or One Thousand and One Lessons in Supersymmetry by Sylvester James GatesSylvester James Gates
Sylvester James Gates, Jr. is a noted American theoretical physicist. He received BS and PhD degrees from Massachusetts Institute of Technology, the latter in 1977. His doctoral thesis was the first thesis at MIT to deal with supersymmetry. Gates is currently the John S...
, Marcus Grisaru, Martin Rocek and Warren Siegel.
In
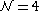superYang-Mills the β-function is zero for all couplings, meaning that the theory is conformalConformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
. This was demonstrated perturbatively by Martin Sohnius and Peter West
Peter West
Peter Anthony West was a BBC presenter and sports commentator best known for his work on the corporation's cricket, tennis and rugby coverage as well as occasionally commentating on field hockey. Throughout his television career he remained freelance.-Early life:He was an only child...
in the 1981 article Conformal Invariance in N=4 Supersymmetric Yang-Mills Theory under certain symmetry assumptions on the theory, and then with no assumptions by Stanley Mandelstam
Stanley Mandelstam
Stanley Mandelstam is a South African-born theoretical physicist. He introduced the relativistically invariant Mandelstam variables into particle physics in 1958 as a convenient coordinate system for formulating his double dispersion relations...
in the 1983 article Light Cone Superspace and the Ultraviolet Finiteness of the N=4 Model. The full nonperturbative proof by Nathan Seiberg
Nathan Seiberg
Nathan "Nati" Seiberg is an Israeli American theoretical physicist who works on string theory. He was recipient of a 1996 MacArthur Fellowship and the Dannie Heineman Prize for Mathematical Physics in 1998. He is currently a professor at the Institute for Advanced Study in Princeton, New Jersey, USA...
appeared in the 1988 article Supersymmetry and Nonperturbative beta Functions.
Examples in 3-dimensional theories
In 3 dimensions the number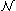 counts the number of 2-component Majorana spinors of supercharges.When
there is no holomorphicity and few exact results are known.When
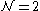the superpotential cannot depend on the linear multiplets and in particular is independent of the Fayet-Iliopoulos terms (FI) and Majorana mass terms. On the other hand the central chargeCentral charge
In theoretical physics, a central charge is an operator Z that commutes with all the other symmetry operators. The adjective "central" refers to the center of the symmetry group -- the subgroup of elements that commute with all other elements of the original group—or to the center of a Lie algebra...
is independent of the chiral multiplets, and so is a linear combination of the FI and Majorana mass terms. These two theorems were stated and proven in Aspects of N=2 Supersymmetric Gauge Theories in Three Dimensions.
When
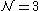, unlike 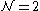, the R-symmetryR-symmetry
In theoretical physics, the R-symmetry is the symmetry transforming different supercharges in a theory with supersymmetry into each other. In the simplest case of the N=1 supersymmetry, such an R-symmetry is isomorphic to a global U group or its discrete subgroup...
is the nonabelian group
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
SU(2) and so the representation
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of each field is not renormalized. In a superconformal field theory the conformal dimension
Conformal dimension
In mathematics, the conformal dimension of a metric space X is the infimum of the Hausdorff dimension over the conformal gauge of X, that is, the class of all metric spaces quasisymmetric to X.-Formal definition:...
of a chiral multiplet
Chiral superfield
In theoretical physics, one often analyzes theories with supersymmetry in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace...
is entirely determined by its R-charge, and so these conformal dimensions are not renormalized. Therefore matter fields have no wave function renormalization
Wave function renormalization
In quantum field theory, wave function renormalization is a rescaling, or renormalization, of quantum fields to take into account the effects of interactions. For a noninteracting or free field, the field operator creates or annihilates a single particle with probability 1. Once interactions are...
in
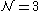superconformal field theories, as was shown in On Mirror Symmetry in Three Dimensional Abelian Gauge Theories. These theories consist of vector multiplets and hypermultiplets. The hypermultiplet metric is hyperkähler and may not be lifted by quantum corrections, but its metric may be modified. No renormalizableRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
interaction between hyper and abelian vector multiplets is possible except for Chern-Simons terms
Chern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
.
When
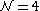, unlike 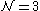the hypermultiplet metric may no longer be modified by quantum corrections.Examples in 2-dimensional theories
In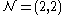 linear sigma models, which are superrenormalizable abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
gauge theories with matter in chiral supermultiplet
Chiral superfield
In theoretical physics, one often analyzes theories with supersymmetry in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace...
s, Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
has argued in Phases of N=2 theories in two-dimensions that the only divergent quantum correction is the logarithmic
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
one-loop correction to the FI term.
Nonrenormalization from a quantization condition
In supersymmetric and nonsupersymmetric theories, the nonrenormalization of a quantity subject to the Dirac quantization condition is often a consequence of the fact that possible renormalizations would be inconsistent with the quantization condition, for example the quantization of the level of a Chern-Simons theoryChern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
implies that it may only be renormalized at one-loop. In the 1994 article Nonrenormalization Theorem for Gauge Coupling in 2+1D the authors find the renormalization of the level can only be a finite shift, independent of the energy scale, and extended this result to topologically massive theories in which one includes a kinetic term
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
for the gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s. In Notes on Superconformal Chern-Simons-Matter Theories the authors then showed that this shift needs to occur at one loop, because any renormalization at higher loops would introduce inverse powers of the level, which are nonintegral and so would be in conflict with the quantization condition.