Technicolor (physics)
Encyclopedia
Technicolor theories are models of physics
beyond the standard model
that address electroweak symmetry breaking, the mechanism through which elementary particle
s acquire masses. Early technicolor theories were modelled on quantum chromodynamics
(QCD), the "color" theory of the strong nuclear force
, which inspired their name.
Instead of introducing elementary Higgs boson
s to explain observed phenomena, technicolor models hide electroweak
symmetry and generate masses for the W and Z bosons
through the dynamics of new gauge interactions
. Although asymptotically free
at very high energies, these interactions must become strong and confining (and hence unobservable) at lower energies that have been experimentally probed. This dynamical approach is natural
and avoids the hierarchy problem
of the Standard Model.
In order to produce quark
and lepton
masses, technicolor has to be "extended" by additional gauge interactions. Particularly when modelled on QCD, extended technicolor is challenged by experimental constraints on flavor-changing neutral current and precision electroweak measurements
. It is not known what is the extended technicolor dynamics.
Much technicolor research focuses on exploring strongly-interacting gauge theories other than QCD, in order to evade some of these challenges. A particularly active framework is "walking" technicolor, which exhibits nearly-conformal
behavior caused by an infrared fixed point
with strength just above that necessary for spontaneous chiral symmetry
breaking. Whether walking can occur and lead to agreement with precision electroweak measurements is being studied through non-perturbative lattice
simulations.
Experiments at the Large Hadron Collider
are expected to discover the mechanism responsible for electroweak symmetry breaking, and will be critical for determining whether the technicolor framework provides the correct description of nature.
gauge symmetry
in the Standard Model
of elementary particle interactions remains unknown. The breaking must be spontaneous
, meaning that the underlying theory manifests the symmetry exactly (the gauge-boson fields are massless in the equations of motion), but the solutions (the ground state and the excited states) do not. In particular, the physical W and Z gauge bosons
become massive. This phenomenon, in which the W and Z bosons also acquire an extra polarization state, is called the "Higgs mechanism". Despite the precise agreement of the electroweak theory with experiment at energies accessible so far, the necessary ingredients for the symmetry breaking remain hidden, yet to be revealed at higher energies.
The simplest mechanism of electroweak symmetry breaking introduces a single complex field and predicts the existence of the Higgs boson
. Typically, the Higgs boson is "unnatural" in the sense that quantum mechanical fluctuations produce corrections to its mass that lift it to such high values that it cannot play the role for which it was introduced. Unless the Standard Model breaks down at energies less than a few TeV, the Higgs mass can be kept small only by a delicate fine-tuning
of parameters.
Technicolor avoids this problem by hypothesizing a new gauge interaction coupled to new massless fermions. This interaction is asymptotically free
at very high energies and becomes strong and confining as the energy decreases to the electroweak scale of roughly 250 GeV. These strong forces spontaneously break the massless fermions' chiral symmetries, some of which are weakly gauged as part of the Standard Model. This is the dynamical version of the Higgs mechanism. The electroweak gauge symmetry is thus broken, producing masses for the W and Z bosons.
The new strong interaction leads to a host of new composite, short-lived particles at energies accessible at the Large Hadron Collider
(LHC). This framework is natural because there are no elementary Higgs bosons and, hence, no fine-tuning of parameters. Quark and lepton masses also break the electroweak gauge symmetries, so they, too, must arise spontaneously. A mechanism for incorporating this feature is known as extended technicolor. Technicolor and extended technicolor face a number of phenomenological challenges. Some of them can be addressed within a class of theories known as walking technicolor.
). The quadratic divergence in the scalar's mass requires adjustments of a part in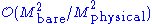
, where Mbare is the cutoff of the theory, the energy scale at which the theory changes in some essential way. In the standard electroweak model with Mbare ∼ 1015 GeV (the grand-unification mass scale), and with the Higgs boson
mass Mphysical = 100–500 GeV, the mass is tuned to at least a part in 1025.
By contrast, a natural theory of electroweak symmetry breaking is an asymptotically-free gauge theory with fermions as the only matter fields. The technicolor gauge group GTC is often assumed to be SU(NTC). Based on analogy with quantum chromodynamics (QCD), it is assumed that there are one or more doublets of massless Dirac "technifermions" transforming vectorially under the same complex representation
of GTC, TiL,R = (Ui,Di)L,R, i = 1,2, … ,Nf/2. Thus, there is a chiral symmetry
of these fermions, e.g., SU(Nf)L ⊗ SU(Nf)R, if they all transform according the same complex representation of GTC. Continuing the analogy with QCD, the running gauge coupling αTC(μ) triggers spontaneous chiral symmetry breaking, the technifermions acquire a dynamical mass, and a number of massless Goldstone boson
s result. If the technifermions transform under [SU(2) ⊗ U(1)]EW as left-handed doublets and right-handed singlets, three linear combinations of these Goldstone bosons couple to three of the electroweak gauge currents.
In 1973 Jackiw and Johnson and Cornwall and Norton studied the possibility that a (non-vectorial) gauge interaction of fermions can break itself; i.e., is strong enough to form a Goldstone boson coupled to the gauge current. Using Abelian gauge models, they showed that, if such a Goldstone boson is formed, it is "eaten" by the Higgs mechanism, becoming the longitudinal component of the now massive gauge boson. Technically, the polarization function Π(p2) appearing in the gauge boson propagator, Δμν = (pμ pν/p2 - gμν)/[p2(1 Ð g2 Π(p2))] develops a pole at p2 = 0 with residue F2, the square of the Goldstone boson's decay constant, and the gauge boson acquires mass M ≅ g F. In 1973, Weinstein showed that composite Goldstone bosons whose constituent fermions transform in the “standard” way under SU(2) ⊗ U(1) generate the weak boson masses
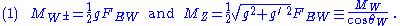
This standard-model relation is achieved with elementary Higgs bosons in electroweak doublets; it is verified experimentally to better than 1%. Here, g and g′ are SU(2) and U(1) gauge couplings and tanθW = g′/g defines the weak mixing angle.
The important idea of a new strong gauge interaction of massless fermions at the electroweak scale FEW driving the spontaneous breakdown of its global chiral symmetry, of which an SU(2) ⊗ U(1) subgroup is weakly gauged, was first proposed in 1979 by S. Weinberg and L. Susskind. This "technicolor" mechanism is natural in that no fine-tuning
of parameters is necessary.
s perform another important task. In the Standard Model
, quark
s and lepton
s are necessarily massless because they transform under SU(2) ⊗ U(1) as left-handed doublets and right-handed singlets. The Higgs doublet couples to these fermions. When it develops its vacuum expectation value, it transmits this electroweak
breaking to the quarks and leptons, giving them their observed masses. (In general, electroweak-eigenstate fermions are not mass eigenstates, so this process also induces the mixing matrices observed in charged-current weak interactions.)
In technicolor, something else must generate the quark and lepton masses. The only natural possibility, one avoiding the introduction of elementary scalars, is to enlarge GTC to allow technifermions to couple to quarks and leptons. This coupling is induced by gauge bosons of the enlarged group. The picture, then, is that there is a large "extended technicolor" (ETC) gauge group GETC ⊃ GTC in which technifermions, quarks, and leptons live in the same representations
. At one or more high scales ΛETC, GETC is broken down to GTC, and quarks and leptons emerge as the TC-singlet fermions. When αTC(μ) becomes strong at scale ΛTC ≅ FEW, the fermionic condensate
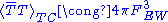forms. (The condensate is the vacuum expectation value
of the technifermion bilinear
. The estimate here is based on naive dimensional analysis of the quark condensate in QCD
, expected to be correct as an order of magnitude.) Then, the transitions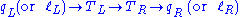
can proceed through the technifermion's dynamical mass by the emission and reabsorption of ETC bosons whose masses METC ≅ gETC ΛETC are much greater than ΛTC. The quarks and leptons develop masses given approximately by
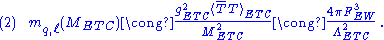
Here,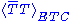
is the technifermion condensate renormalized at the ETC boson mass scale,
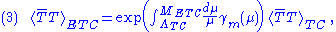
where γm(μ) is the anomalous dimension
of the technifermion bilinear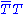
at the scale μ. The second estimate in Eq. (2) depends on the assumption that, as happens in QCD, αTC(μ) becomes weak not far above ΛTC, so that the anomalous dimension γm of 
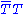is small there. Extended technicolor was introduced in 1979 by Dimopoulos and Susskind, and by Eichten and Lane. For a quark of mass mq ≅ 1 GeV, and with ΛTC ≅ 250 GeV, one estimates ΛETC ≅ 15 TeV. Therefore, assuming that 
, METC will be at least this large.
In addition to the ETC proposal for quark and lepton masses, Eichten and Lane observed that the size of the ETC representations required to generate all quark and lepton masses suggests that there will be more than one electroweak doublet of technifermions. If so, there will be more (spontaneously broken) chiral symmetries and therefore more Goldstone boson
s than are eaten by the Higgs mechanism. These must acquire mass by virtue of the fact that the extra chiral symmetries are also explicitly broken, by the standard-model interactions and the ETC interactions. These "pseudo-Goldstone bosons" are called technipions, πT. An application of Dashen's theorem gives for the ETC contribution to their mass
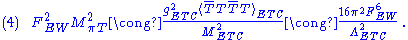
The second approximation in Eq. (4) assumes that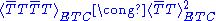
. For FEW ≅ ΛTC ≅ 250 GeV and ΛETC ≅ 15 TeV, this contribution to MπT is about 50 GeV. Since ETC interactions generate 
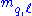and the coupling of technipions to quark and lepton pairs, one expects the couplings to be Higgs-like; i.e., roughly proportional to the masses of the quarks and leptons. This means that technipions are expected to decay to the heaviest 
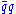and 
pairs allowed.
Perhaps the most important restriction on the ETC framework for quark mass generation is that ETC interactions are likely to induce flavor-changing neutral current processes such as μ → e γ, KL → μ e, and |Δ S| = 2 and |Δ B| = 2 interactions that induce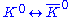
and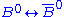 
mixing. The reason is that the algebra of the ETC currents involved in 
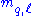generation imply 
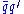and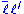 
ETC currents which, when written in terms of fermion mass eigenstates, have no reason to conserve flavor. The strongest constraint comes from requiring that ETC interactions mediating 
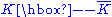mixing contribute less than the Standard Model. This implies an effective ΛETC greater than 1000 TeV. The actual ΛETC may be reduced somewhat if CKM-like mixing angle factors are present. If these interactions are CP-violating, as they well may be, the constraint from the ε-parameter is that the effective ΛETC > 104 TeV. Such huge ETC mass scales imply tiny quark and lepton masses and ETC contributions to MπT of at most a few GeV, in conflict with LEP
searches for πT at the Z0.
Extended technicolor is a very ambitious proposal, requiring that quark and lepton masses and mixing angles arise from experimentally accessible interactions. If there exists a successful model, it would not only predict the masses and mixings of quarks and leptons (and technipions), it would explain why there are three families of each: they are the ones that fit into the ETC representations of q,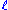
and T. It should not be surprising that the construction of a successful model has proven to be very difficult.
.
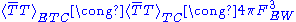During the 1980s, several dynamical mechanisms were advanced to do this. In 1981 Holdom suggested that, if the αTC(μ) evolves to a nontrivial fixed point in the ultraviolet, with a large positive anomalous dimension
γm for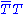
, realistic quark and lepton masses could arise with ΛETC large enough to suppress ETC-induced 
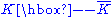mixing. However, no example of a nontrivial ultraviolet fixed point
in a four-dimensional gauge theory has been constructed. In 1985 Holdom analyzed a technicolor theory in which a “slowly varying” αTC(μ) was envisioned. His focus was to separate the chiral breaking and confinement scales, but he also noted that such a theory could enhance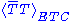
and thus allow the ETC scale to be raised. In 1986 Akiba and Yanagida also considered enhancing quark and lepton masses, by simply assuming that αTC is constant and strong all the way up to the ETC scale. In the same year Yamawaki, Bando and Matumoto again imagined an ultraviolet fixed point in a non-asymptotically free
theory to enhance the technifermion condensate.
In 1986 Appelquist, Karabali and Wijewardhana discussed the enhancement of fermion masses in an asymptotically free technicolor theory with a slowly running, or “walking”, gauge coupling. The slowness arose from the screening effect of a large number of technifermions, with the analysis carried out through two-loop perturbation theory. In 1987 Appelquist and Wijewardhana explored this walking scenario further. They took the analysis to three loops, noted that the walking can lead to a power law enhancement of the technifermion condensate, and estimated the resultant quark, lepton, and technipion masses. The condensate enhancement arises because the associated technifermion mass decreases slowly, roughly linearly, as a function of its renormalization scale. This corresponds to the condensate anomalous dimension γm in Eq. (3) approaching unity (see below).
In the 1990s, the idea emerged more clearly that walking is naturally described by asymptotically free gauge theories dominated in the infrared by an approximate fixed point. Unlike the speculative proposal of ultraviolet fixed points, fixed points in the infrared are known to exist in asymptotically free theories, arising at two loops in the beta function providing that the fermion count Nf is large enough. This has been known since the first two-loop computation in 1974 by Caswell. If Nf is close to the value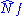
at which asymptotic freedom is lost, the resultant infrared fixed point is weak, of parametric order 
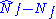, and reliably accessible in perturbation theory. This weak-coupling limit was explored by Banks and Zaks in 1982.
The fixed-point coupling αIR becomes stronger as Nf is reduced from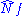
. Below some critical value Nfc the coupling becomes strong enough (> αχ SB) to break spontaneously the massless technifermions' chiral symmetry
. Since the analysis must typically go beyond two-loop perturbation theory, the definition of the running coupling αTC(μ), it’s fixed point value αIR, and the strength αχ SB necessary for chiral symmetry breaking depend on the particular renormalization scheme adopted. For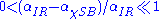
; i.e., for Nf just below Nfc, the evolution of αTC(μ) is governed by the infrared fixed point
and it will evolve slowly (walk) for a range of momenta above the breaking scale ΛTC. To overcome the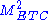
-suppression of the masses of first and second generation quarks involved in 
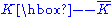mixing, this range must extend almost to their ETC scale, of 
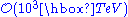. Cohen and Georgi argued that γm = 1 is the signal of spontaneous chiral symmetry breaking, i.e., that γm(αχ SB) = 1. Therefore, in the walking-αTC region, γm ≅ 1 and, from Eqs. (2) and (3), the light quark masses are enhanced approximately by METC/ΛTC.
The idea that αTC(μ) walks for a large range of momenta when αIR lies just above αχ SB was suggested by Lane and Ramana. They made an explicit model, discussed the walking that ensued, and used it in their discussion of walking technicolor phenomenology at hadron colliders. This idea was developed in some detail by Appelquist, Terning and Wijewardhana. Combining a perturbative computation of the infrared fixed point with an approximation of αχ SB based on the Schwinger-Dyson equation
, they estimated the critical value Nfc and explored the resultant electroweak
physics. Since the 1990s, most discussions of walking technicolor are in the framework of theories assumed to be dominated in the infrared by an approximate fixed point. Various models have been explored, some with the technifermions in the fundamental representation
of the gauge group and some employing higher representations.
The possibility that the technicolor condensate can be enhanced beyond that discussed in the walking literature, has also been considered recently by Luty and Okui under the name "conformal technicolor". They envision an infrared stable fixed point, but with a very large anomalous dimension
for the operator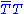
. It remains to be seen whether this can be realized, for example, in the class of theories currently being examined using lattice techniques.
mass, even for an ETC scale as low as a few TeV. However, this problem could be addressed if the effective four-technifermion coupling resulting from ETC gauge boson exchange is strong and tuned just above a critical value. The analysis of this strong-ETC possibility is that of a Nambu–Jona–Lasinio model with an additional (technicolor) gauge interaction. The technifermion masses are small compared to the ETC scale (the cutoff on the effective theory), but nearly constant out to this scale, leading to a large top quark mass. No fully realistic ETC theory for all quark masses has yet been developed incorporating these ideas. A related study was carried out by Miransky and Yamawaki. A problem with this approach is that it involves some degree of parameter fine-tuning
, in conflict with technicolor’s guiding principle of naturalness.
Finally, it should be noted that there is a large body of closely related work in which ETC does not generate mt. These are the top quark condensate
, topcolor
and top-color-assisted technicolor models, in which new strong interactions are ascribed to the top quark and other third-generation fermions. As with the strong-ETC scenario described above, all these proposals involve a considerable degree of fine-tuning of gauge couplings.
and Kimmo Tuominen proposed technicolor models with technifermions in higher-dimensional representations of the technicolor gauge group. They argued that these more "minimal" models required fewer flavors of technifermions in order to exhibit walking behavior, making it easier to pass precision electroweak tests.
For example, SU(2) and SU(3) gauge theories may exhibit walking with as few as two Dirac flavors of fermions in the adjoint or two-index symmetric representation. In contrast, at least eight flavors of fermions in the fundamental representation of SU(3) (and possibly SU(2) as well) are required to reach the near-conformal regime.
These results continue to be investigated by various methods, including lattice simulations discussed below, which have confirmed the near-conformal dynamics of these minimal walking models. The first comprehensive effective Lagrangian for minimal walking models, featuring a light composite Higgs, spin-one states, tree-level unitarity
, and consistency with phenomenological constraints was constructed in 2007 by Foadi, Frandsen, Ryttov and Sannino.
is a non-perturbative method applicable to strongly-interacting technicolor theories, allowing first-principles exploration of walking and conformal dynamics. In 2007, Catterall and Sannino used lattice gauge theory to study SU(2) gauge theories with two flavors of Dirac fermions in the symmetric representation, finding evidence of conformality that has been confirmed by subsequent studies.
As of 2010, the situation for SU(3) gauge theory with fermions in the fundamental representation is not as clear-cut. In 2007, Appelquist, Fleming and Neil reported evidence that a non-trivial infrared fixed point develops in such theories when there are twelve flavors, but not when there are eight. While some subsequent studies confirmed these results, others reported different conclusions, depending on the lattice methods used, and there is not yet consensus.
Further lattice studies exploring these issues, as well as considering the consequences of these theories for precision electroweak measurements
, are underway by several research groups.
must conform with precision measurements of the electroweak parameters. Its consequences for physics at existing and future high-energy hadron colliders, and for the dark matter of the universe must also be explored.
were introduced by Peskin and Takeuchi to quantify contributions to electroweak radiative corrections from physics beyond the Standard Model. They have a simple relation to the parameters of the electroweak chiral Lagrangian. The Peskin-Takeuchi analysis was based on the general formalism for weak radiative corrections developed by Kennedy, Lynn, Peskin and Stuart, and alternate formulations also exist.
The S, T, and U-parameters describe corrections to the electroweak gauge boson propagators from physics Beyond the Standard Model
. They can be written in terms of polarization functions of electroweak currents and their spectral representation as follows:
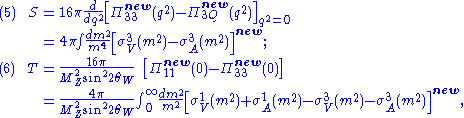
where only new, beyond-standard-model physics is included. The quantities are calculated relative to a minimal Standard Model with some chosen reference mass of the Higgs boson
, taken to range from the experimental lower bound of 117 GeV to 1000 GeV where its width becomes very large. For these parameters to describe the dominant corrections to the Standard Model, the mass scale of the new physics must be much greater than MW and MZ, and the coupling of quark
s and lepton
s to the new particles must be suppressed relative to their coupling to the gauge bosons. This is the case with technicolor, so long as the lightest technivector mesons, ρT and aT, are heavier than 200–300 GeV. The S-parameter is sensitive to all new physics at the TeV scale, while T is a measure of weak-isospin breaking effects. The U-parameter is generally not useful; most new-physics theories, including technicolor theories, give negligible contributions to it.
The S and T-parameters are determined by global fit to experimental data including Z-pole data from LEP
at CERN
, top quark and W-mass measurements at Fermilab, and measured levels of atomic parity violation. The resultant bounds on these parameters are given in the Review of Particle Properties. Assuming U = 0, the S and T parameters are small and, in fact, consistent with zero:
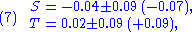
where the central value corresponds to a Higgs mass of 117 GeV and the correction to the central value when the Higgs mass is increased to 300 GeV is given in parentheses. These values place tight restrictions on beyond-standard-model theories—when the relevant corrections can be reliably computed.
The S parameter estimated in QCD
-like technicolor theories is significantly greater than the experimentally-allowed value. The computation was done assuming that the spectral integral for S is dominated by the lightest ρT and aT resonances, or by scaling effective Lagrangian parameters from QCD. In walking technicolor, however, the physics at the TeV scale and beyond must be quite different from that of QCD-like theories. In particular, the vector and axial-vector spectral functions cannot be dominated by just the lowest-lying resonances. It is unknown whether higher energy contributions to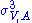
are a tower of identifiable ρT and aT states or a smooth continuum. It has been conjectured that ρT and aT partners could be more nearly degenerate in walking theories (approximate parity doubling), reducing their contribution to S. Lattice
calculations are underway or planned to test these ideas and obtain reliable estimates of S in walking theories.
The restriction on the T-parameter poses a problem for the generation of the top-quark mass in the ETC framework. The enhancement from walking can allow the associated ETC scale to be as large as a few TeV, but—since the ETC interactions must be strongly weak-isospin breaking to allow for the large top-bottom mass splitting—the contribution to the T parameter, as well as the rate for the decay
, could be too large.
doublet of technifermions, or one techni-family including one doublet each of color-triplet techniquarks and color-singlet technileptons. In the minimal, one-doublet model, three Goldstone boson
s (technipions, πT) have decay constant F = FEW = 246 GeV and are eaten by the electroweak gauge bosons. The most accessible collider signal is the production through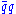
annihilation in a hadron collider of spin-one 
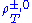, and their subsequent decay into a pair of longitudinally-polarized weak bosons, 
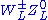and 
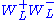. At an expected mass of 1.5–2.0 TeV and width of 300–400 GeV, such ρT's would be difficult to discover at the LHC. A one-family model has a large number of physical technipions, with F = FEW/ = 123 GeV. There is a collection of correspondingly lower-mass color-singlet and octet technivectors decaying into technipion pairs. The πT's are expected to decay to the heaviest possible quark and lepton pairs. Despite their lower masses, the ρT's are wider than in the minimal model and the backgrounds to the πT decays are likely to be insurmountable at a hadron collider.
This picture changed with the advent of walking technicolor. A walking gauge coupling occurs if αχ SB lies just below the IR fixed point value αIR, which requires either a large number of electroweak doublets in the fundamental representation
of the gauge group, e.g., or a few doublets in higher-dimensional TC representations. In the latter case, the constraints on ETC representations generally imply other technifermions in the fundamental representation as well. In either case, there are technipions πT with decay constant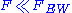
. This implies 
so that the lightest technivectors accessible at the LHC—ρT, ωT, aT (with IG JPC = 1+ 1−−, 0− 1−−, 1− 1++)—have masses well below a TeV. The class of theories with many technifermions and thus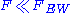 
is called low-scale technicolor.
A second consequence of walking technicolor concerns the decays of the spin-one technihadrons. Since technipion masses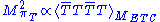
(see Eq. (4)), walking enhances them much more than it does other technihadron masses. Thus, it is very likely that the lightest MρT < 2MπT and that the two and three-πT decay channels of the light technivectors are closed. This further implies that these technivectors are very narrow. Their most probable two-body channels are 
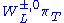, WL WL, γ πT and γ WL. The coupling of the lightest technivectors to WL is proportional to F/FEW. Thus, all their decay rates are suppressed by powers of 
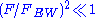or the fine-structure constant, giving total widths of a few GeV (for ρT) to a few tenths of a GeV (for ωT and T).
A more speculative consequence of walking technicolor is motivated by consideration of its contribution to the S-parameter. As noted above, the usual assumptions made to estimate STC are invalid in a walking theory. In particular, the spectral integrals used to evaluate STC cannot be dominated by just the lowest-lying ρT and aT and, if STC is to be small, the masses and weak-current couplings of the ρT and aT could be more nearly equal than they are in QCD.
Low-scale technicolor phenomenology, including the possibility of a more parity-doubled spectrum, has been developed into a set of rules and decay amplitudes. An April 2011 announcement of an excess in jet pairs produced in association with a W boson measured at the Tevatron
has been interpreted by Eichten, Lane and Martin as a possible signal of the technipion of low-scale technicolor.
The general scheme of low-scale technicolor makes little sense if the limit on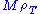
is pushed past about 700 GeV. The LHC should be able to discover it or rule it out. Searches there involving decays to technipions and thence to heavy quark jets are hampered by backgrounds from 
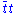production; its rate is 100 times larger than that at the Tevatron. Consequently, the discovery of low-scale technicolor at the LHC relies on all-leptonic final-state channels with favorable signal-to-background ratios: 
, 
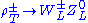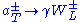and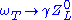 
.
candidates. Almost certainly, models can be built in which the lowest-lying technibaryon, a technicolor-singlet bound state of technifermions, is stable enough to survive the evolution of the universe. If the technicolor theory is low-scale (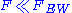
), the baryon's mass should be no more than 1–2 TeV. If not, it could be much heavier. The technibaryon must be electrically neutral and satisfy constraints on its abundance. Given the limits on spin-independent dark-matter-nucleon cross sections from dark-matter search experiments (
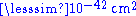for the masses of interest), it may have to be electroweak neutral (weak isospin I = 0) as well. These considerations suggest that the "old" technicolor dark matter candidates may be difficult to produce at the LHC.
A different class of technicolor dark matter candidates light enough to be accessible at the LHC was introduced by Francesco Sannino
and his collaborators. These states are pseudo Goldstone bosons possessing a global charge that makes them stable against decay.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
beyond the standard model
Beyond the Standard Model
Physics beyond the Standard Model refers to the theoretical developments needed to explain the deficiencies of the Standard Model, such as the origin of mass, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy...
that address electroweak symmetry breaking, the mechanism through which elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s acquire masses. Early technicolor theories were modelled on quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
(QCD), the "color" theory of the strong nuclear force
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
, which inspired their name.
Instead of introducing elementary Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
s to explain observed phenomena, technicolor models hide electroweak
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
symmetry and generate masses for the W and Z bosons
W and Z bosons
The W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
through the dynamics of new gauge interactions
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
. Although asymptotically free
Asymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
at very high energies, these interactions must become strong and confining (and hence unobservable) at lower energies that have been experimentally probed. This dynamical approach is natural
Naturalness (physics)
Naturalness is the property that all parameters appearing in a theory take values of order 1...
and avoids the hierarchy problem
Hierarchy problem
In theoretical physics, a hierarchy problem occurs when the fundamental parameters of some Lagrangian are vastly different than the parameters measured by experiment. This can happen because measured parameters are related to the fundamental parameters by a prescription known as renormalization...
of the Standard Model.
In order to produce quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
and lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
masses, technicolor has to be "extended" by additional gauge interactions. Particularly when modelled on QCD, extended technicolor is challenged by experimental constraints on flavor-changing neutral current and precision electroweak measurements
Peskin-Takeuchi parameter
In particle physics, the Peskin–Takeuchi parameters are a set of three measurable quantities, called S, T, and U, that parameterize potential new physics contributions to electroweak radiative corrections...
. It is not known what is the extended technicolor dynamics.
Much technicolor research focuses on exploring strongly-interacting gauge theories other than QCD, in order to evade some of these challenges. A particularly active framework is "walking" technicolor, which exhibits nearly-conformal
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
behavior caused by an infrared fixed point
Infrared fixed point
In physics, an infrared fixed point is a set of coupling constants, or other parameters that evolve from initial values at very high energies , to fixed stable values, usually predictable, at low energies...
with strength just above that necessary for spontaneous chiral symmetry
Chiral symmetry
In quantum field theory, chiral symmetry is a possible symmetry of the Lagrangian under which the left-handed and right-handed parts of Dirac fields transform independently...
breaking. Whether walking can occur and lead to agreement with precision electroweak measurements is being studied through non-perturbative lattice
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
simulations.
Experiments at the Large Hadron Collider
Large Hadron Collider
The Large Hadron Collider is the world's largest and highest-energy particle accelerator. It is expected to address some of the most fundamental questions of physics, advancing the understanding of the deepest laws of nature....
are expected to discover the mechanism responsible for electroweak symmetry breaking, and will be critical for determining whether the technicolor framework provides the correct description of nature.
Introduction
The mechanism for the breaking of electroweakElectroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
gauge symmetry
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
in the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of elementary particle interactions remains unknown. The breaking must be spontaneous
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
, meaning that the underlying theory manifests the symmetry exactly (the gauge-boson fields are massless in the equations of motion), but the solutions (the ground state and the excited states) do not. In particular, the physical W and Z gauge bosons
W and Z bosons
The W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
become massive. This phenomenon, in which the W and Z bosons also acquire an extra polarization state, is called the "Higgs mechanism". Despite the precise agreement of the electroweak theory with experiment at energies accessible so far, the necessary ingredients for the symmetry breaking remain hidden, yet to be revealed at higher energies.
The simplest mechanism of electroweak symmetry breaking introduces a single complex field and predicts the existence of the Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
. Typically, the Higgs boson is "unnatural" in the sense that quantum mechanical fluctuations produce corrections to its mass that lift it to such high values that it cannot play the role for which it was introduced. Unless the Standard Model breaks down at energies less than a few TeV, the Higgs mass can be kept small only by a delicate fine-tuning
Fine-tuning
In theoretical physics, fine-tuning refers to circumstances when the parameters of a model must be adjusted very precisely in order to agree with observations. Theories requiring fine-tuning are regarded as problematic in the absence of a known mechanism to explain why the parameters happen to...
of parameters.
Technicolor avoids this problem by hypothesizing a new gauge interaction coupled to new massless fermions. This interaction is asymptotically free
Asymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
at very high energies and becomes strong and confining as the energy decreases to the electroweak scale of roughly 250 GeV. These strong forces spontaneously break the massless fermions' chiral symmetries, some of which are weakly gauged as part of the Standard Model. This is the dynamical version of the Higgs mechanism. The electroweak gauge symmetry is thus broken, producing masses for the W and Z bosons.
The new strong interaction leads to a host of new composite, short-lived particles at energies accessible at the Large Hadron Collider
Large Hadron Collider
The Large Hadron Collider is the world's largest and highest-energy particle accelerator. It is expected to address some of the most fundamental questions of physics, advancing the understanding of the deepest laws of nature....
(LHC). This framework is natural because there are no elementary Higgs bosons and, hence, no fine-tuning of parameters. Quark and lepton masses also break the electroweak gauge symmetries, so they, too, must arise spontaneously. A mechanism for incorporating this feature is known as extended technicolor. Technicolor and extended technicolor face a number of phenomenological challenges. Some of them can be addressed within a class of theories known as walking technicolor.
Early technicolor
Technicolor is the name given to the theory of electroweak symmetry breaking by new strong gauge-interactions whose characteristic energy scale ΛTC is the weak scale itself, ΛTC ≅ FEW ≡ 246 GeV. The guiding principle of technicolor is "naturalness": basic physical phenomena should not require fine-tuning of the parameters in the Lagrangian that describes them. What constitutes fine-tuning is to some extent a subjective matter, but a theory with elementary scalar particles typically is very finely tuned (unless it is supersymmetricSupersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
). The quadratic divergence in the scalar's mass requires adjustments of a part in
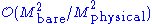, where Mbare is the cutoff of the theory, the energy scale at which the theory changes in some essential way. In the standard electroweak model with Mbare ∼ 1015 GeV (the grand-unification mass scale), and with the Higgs bosonHiggs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
mass Mphysical = 100–500 GeV, the mass is tuned to at least a part in 1025.
By contrast, a natural theory of electroweak symmetry breaking is an asymptotically-free gauge theory with fermions as the only matter fields. The technicolor gauge group GTC is often assumed to be SU(NTC). Based on analogy with quantum chromodynamics (QCD), it is assumed that there are one or more doublets of massless Dirac "technifermions" transforming vectorially under the same complex representation
Complex representation
The term complex representation has slightly different meanings in mathematics and physics.In mathematics, a complex representation is a group representationof a group on a complex vector space....
of GTC, TiL,R = (Ui,Di)L,R, i = 1,2, … ,Nf/2. Thus, there is a chiral symmetry
Chiral symmetry
In quantum field theory, chiral symmetry is a possible symmetry of the Lagrangian under which the left-handed and right-handed parts of Dirac fields transform independently...
of these fermions, e.g., SU(Nf)L ⊗ SU(Nf)R, if they all transform according the same complex representation of GTC. Continuing the analogy with QCD, the running gauge coupling αTC(μ) triggers spontaneous chiral symmetry breaking, the technifermions acquire a dynamical mass, and a number of massless Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
s result. If the technifermions transform under [SU(2) ⊗ U(1)]EW as left-handed doublets and right-handed singlets, three linear combinations of these Goldstone bosons couple to three of the electroweak gauge currents.
In 1973 Jackiw and Johnson and Cornwall and Norton studied the possibility that a (non-vectorial) gauge interaction of fermions can break itself; i.e., is strong enough to form a Goldstone boson coupled to the gauge current. Using Abelian gauge models, they showed that, if such a Goldstone boson is formed, it is "eaten" by the Higgs mechanism, becoming the longitudinal component of the now massive gauge boson. Technically, the polarization function Π(p2) appearing in the gauge boson propagator, Δμν = (pμ pν/p2 - gμν)/[p2(1 Ð g2 Π(p2))] develops a pole at p2 = 0 with residue F2, the square of the Goldstone boson's decay constant, and the gauge boson acquires mass M ≅ g F. In 1973, Weinstein showed that composite Goldstone bosons whose constituent fermions transform in the “standard” way under SU(2) ⊗ U(1) generate the weak boson masses
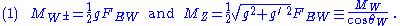
This standard-model relation is achieved with elementary Higgs bosons in electroweak doublets; it is verified experimentally to better than 1%. Here, g and g′ are SU(2) and U(1) gauge couplings and tanθW = g′/g defines the weak mixing angle.
The important idea of a new strong gauge interaction of massless fermions at the electroweak scale FEW driving the spontaneous breakdown of its global chiral symmetry, of which an SU(2) ⊗ U(1) subgroup is weakly gauged, was first proposed in 1979 by S. Weinberg and L. Susskind. This "technicolor" mechanism is natural in that no fine-tuning
Fine-tuning
In theoretical physics, fine-tuning refers to circumstances when the parameters of a model must be adjusted very precisely in order to agree with observations. Theories requiring fine-tuning are regarded as problematic in the absence of a known mechanism to explain why the parameters happen to...
of parameters is necessary.
Extended technicolor
Elementary Higgs bosonHiggs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
s perform another important task. In the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s and lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s are necessarily massless because they transform under SU(2) ⊗ U(1) as left-handed doublets and right-handed singlets. The Higgs doublet couples to these fermions. When it develops its vacuum expectation value, it transmits this electroweak
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
breaking to the quarks and leptons, giving them their observed masses. (In general, electroweak-eigenstate fermions are not mass eigenstates, so this process also induces the mixing matrices observed in charged-current weak interactions.)
In technicolor, something else must generate the quark and lepton masses. The only natural possibility, one avoiding the introduction of elementary scalars, is to enlarge GTC to allow technifermions to couple to quarks and leptons. This coupling is induced by gauge bosons of the enlarged group. The picture, then, is that there is a large "extended technicolor" (ETC) gauge group GETC ⊃ GTC in which technifermions, quarks, and leptons live in the same representations
Representation of a Lie group
In mathematics and theoretical physics, the idea of a representation of a Lie group plays an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie...
. At one or more high scales ΛETC, GETC is broken down to GTC, and quarks and leptons emerge as the TC-singlet fermions. When αTC(μ) becomes strong at scale ΛTC ≅ FEW, the fermionic condensate
Fermionic condensate
A fermionic condensate is a superfluid phase formed by fermionic particles at low temperatures. It is closely related to the Bose–Einstein condensate, a superfluid phase formed by bosonic atoms under similar conditions. Unlike the Bose–Einstein condensates, fermionic condensates are formed using...
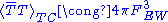forms. (The condensate is the vacuum expectation valueVacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the technifermion bilinear
. The estimate here is based on naive dimensional analysis of the quark condensate in QCDQuantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, expected to be correct as an order of magnitude.) Then, the transitions
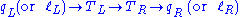can proceed through the technifermion's dynamical mass by the emission and reabsorption of ETC bosons whose masses METC ≅ gETC ΛETC are much greater than ΛTC. The quarks and leptons develop masses given approximately by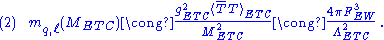Here,
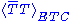is the technifermion condensate renormalized at the ETC boson mass scale,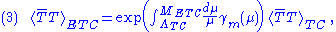where γm(μ) is the anomalous dimension
Anomalous scaling dimension
In theoretical physics, by anomaly one usually means that the symmetry remains broken when the symmetry-breaking factor goes to zero.When the symmetry which is broken is scale invariance, then true power laws usually cannot be found from dimensional reasoning like in turbulence or quantum field...
of the technifermion bilinear
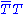at the scale μ. The second estimate in Eq. (2) depends on the assumption that, as happens in QCD, αTC(μ) becomes weak not far above ΛTC, so that the anomalous dimension γm of 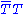is small there. Extended technicolor was introduced in 1979 by Dimopoulos and Susskind, and by Eichten and Lane. For a quark of mass mq ≅ 1 GeV, and with ΛTC ≅ 250 GeV, one estimates ΛETC ≅ 15 TeV. Therefore, assuming that , METC will be at least this large.In addition to the ETC proposal for quark and lepton masses, Eichten and Lane observed that the size of the ETC representations required to generate all quark and lepton masses suggests that there will be more than one electroweak doublet of technifermions. If so, there will be more (spontaneously broken) chiral symmetries and therefore more Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
s than are eaten by the Higgs mechanism. These must acquire mass by virtue of the fact that the extra chiral symmetries are also explicitly broken, by the standard-model interactions and the ETC interactions. These "pseudo-Goldstone bosons" are called technipions, πT. An application of Dashen's theorem gives for the ETC contribution to their mass
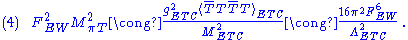
The second approximation in Eq. (4) assumes that
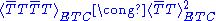. For FEW ≅ ΛTC ≅ 250 GeV and ΛETC ≅ 15 TeV, this contribution to MπT is about 50 GeV. Since ETC interactions generate 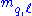and the coupling of technipions to quark and lepton pairs, one expects the couplings to be Higgs-like; i.e., roughly proportional to the masses of the quarks and leptons. This means that technipions are expected to decay to the heaviest 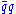and pairs allowed.Perhaps the most important restriction on the ETC framework for quark mass generation is that ETC interactions are likely to induce flavor-changing neutral current processes such as μ → e γ, KL → μ e, and |Δ S| = 2 and |Δ B| = 2 interactions that induce
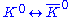and 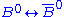mixing. The reason is that the algebra of the ETC currents involved in 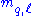generation imply 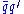and 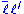ETC currents which, when written in terms of fermion mass eigenstates, have no reason to conserve flavor. The strongest constraint comes from requiring that ETC interactions mediating 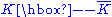mixing contribute less than the Standard Model. This implies an effective ΛETC greater than 1000 TeV. The actual ΛETC may be reduced somewhat if CKM-like mixing angle factors are present. If these interactions are CP-violating, as they well may be, the constraint from the ε-parameter is that the effective ΛETC > 104 TeV. Such huge ETC mass scales imply tiny quark and lepton masses and ETC contributions to MπT of at most a few GeV, in conflict with LEPLarge Electron-Positron Collider
The Large Electron–Positron Collider was one of the largest particle accelerators ever constructed.It was built at CERN, a multi-national centre for research in nuclear and particle physics near Geneva, Switzerland. LEP was a circular collider with a circumference of 27 kilometres built in a...
searches for πT at the Z0.
Extended technicolor is a very ambitious proposal, requiring that quark and lepton masses and mixing angles arise from experimentally accessible interactions. If there exists a successful model, it would not only predict the masses and mixings of quarks and leptons (and technipions), it would explain why there are three families of each: they are the ones that fit into the ETC representations of q,
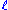and T. It should not be surprising that the construction of a successful model has proven to be very difficult.Walking technicolor
Since quark and lepton masses are proportional to the bilinear technifermion condensate divided by the ETC mass scale squared, their tiny values can be avoided if the condensate is enhanced above the weak-αTC estimate in Eq. (2),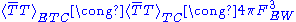.During the 1980s, several dynamical mechanisms were advanced to do this. In 1981 Holdom suggested that, if the αTC(μ) evolves to a nontrivial fixed point in the ultraviolet, with a large positive anomalous dimension
Anomalous scaling dimension
In theoretical physics, by anomaly one usually means that the symmetry remains broken when the symmetry-breaking factor goes to zero.When the symmetry which is broken is scale invariance, then true power laws usually cannot be found from dimensional reasoning like in turbulence or quantum field...
γm for
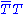, realistic quark and lepton masses could arise with ΛETC large enough to suppress ETC-induced 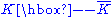mixing. However, no example of a nontrivial ultraviolet fixed pointUV fixed point
In a quantum field theory, one may calculate an effectiveor running coupling constant that defines thecoupling of the theory measured at a given momentum scale.One example of such a coupling constantis the electric charge...
in a four-dimensional gauge theory has been constructed. In 1985 Holdom analyzed a technicolor theory in which a “slowly varying” αTC(μ) was envisioned. His focus was to separate the chiral breaking and confinement scales, but he also noted that such a theory could enhance
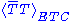and thus allow the ETC scale to be raised. In 1986 Akiba and Yanagida also considered enhancing quark and lepton masses, by simply assuming that αTC is constant and strong all the way up to the ETC scale. In the same year Yamawaki, Bando and Matumoto again imagined an ultraviolet fixed point in a non-asymptotically freeAsymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
theory to enhance the technifermion condensate.
In 1986 Appelquist, Karabali and Wijewardhana discussed the enhancement of fermion masses in an asymptotically free technicolor theory with a slowly running, or “walking”, gauge coupling. The slowness arose from the screening effect of a large number of technifermions, with the analysis carried out through two-loop perturbation theory. In 1987 Appelquist and Wijewardhana explored this walking scenario further. They took the analysis to three loops, noted that the walking can lead to a power law enhancement of the technifermion condensate, and estimated the resultant quark, lepton, and technipion masses. The condensate enhancement arises because the associated technifermion mass decreases slowly, roughly linearly, as a function of its renormalization scale. This corresponds to the condensate anomalous dimension γm in Eq. (3) approaching unity (see below).
In the 1990s, the idea emerged more clearly that walking is naturally described by asymptotically free gauge theories dominated in the infrared by an approximate fixed point. Unlike the speculative proposal of ultraviolet fixed points, fixed points in the infrared are known to exist in asymptotically free theories, arising at two loops in the beta function providing that the fermion count Nf is large enough. This has been known since the first two-loop computation in 1974 by Caswell. If Nf is close to the value
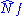at which asymptotic freedom is lost, the resultant infrared fixed point is weak, of parametric order 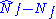, and reliably accessible in perturbation theory. This weak-coupling limit was explored by Banks and Zaks in 1982.The fixed-point coupling αIR becomes stronger as Nf is reduced from
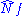. Below some critical value Nfc the coupling becomes strong enough (> αχ SB) to break spontaneously the massless technifermions' chiral symmetryChiral symmetry
In quantum field theory, chiral symmetry is a possible symmetry of the Lagrangian under which the left-handed and right-handed parts of Dirac fields transform independently...
. Since the analysis must typically go beyond two-loop perturbation theory, the definition of the running coupling αTC(μ), it’s fixed point value αIR, and the strength αχ SB necessary for chiral symmetry breaking depend on the particular renormalization scheme adopted. For
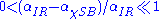; i.e., for Nf just below Nfc, the evolution of αTC(μ) is governed by the infrared fixed pointInfrared fixed point
In physics, an infrared fixed point is a set of coupling constants, or other parameters that evolve from initial values at very high energies , to fixed stable values, usually predictable, at low energies...
and it will evolve slowly (walk) for a range of momenta above the breaking scale ΛTC. To overcome the
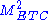-suppression of the masses of first and second generation quarks involved in 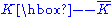mixing, this range must extend almost to their ETC scale, of 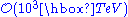. Cohen and Georgi argued that γm = 1 is the signal of spontaneous chiral symmetry breaking, i.e., that γm(αχ SB) = 1. Therefore, in the walking-αTC region, γm ≅ 1 and, from Eqs. (2) and (3), the light quark masses are enhanced approximately by METC/ΛTC.The idea that αTC(μ) walks for a large range of momenta when αIR lies just above αχ SB was suggested by Lane and Ramana. They made an explicit model, discussed the walking that ensued, and used it in their discussion of walking technicolor phenomenology at hadron colliders. This idea was developed in some detail by Appelquist, Terning and Wijewardhana. Combining a perturbative computation of the infrared fixed point with an approximation of αχ SB based on the Schwinger-Dyson equation
Schwinger-Dyson equation
The Schwinger–Dyson equation , also Dyson-Schwinger equations, named after Julian Schwinger and Freeman Dyson, are general relations between Green functions in quantum field theories...
, they estimated the critical value Nfc and explored the resultant electroweak
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
physics. Since the 1990s, most discussions of walking technicolor are in the framework of theories assumed to be dominated in the infrared by an approximate fixed point. Various models have been explored, some with the technifermions in the fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
of the gauge group and some employing higher representations.
The possibility that the technicolor condensate can be enhanced beyond that discussed in the walking literature, has also been considered recently by Luty and Okui under the name "conformal technicolor". They envision an infrared stable fixed point, but with a very large anomalous dimension
Anomalous scaling dimension
In theoretical physics, by anomaly one usually means that the symmetry remains broken when the symmetry-breaking factor goes to zero.When the symmetry which is broken is scale invariance, then true power laws usually cannot be found from dimensional reasoning like in turbulence or quantum field...
for the operator
. It remains to be seen whether this can be realized, for example, in the class of theories currently being examined using lattice techniques.Top quark mass
The walking enhancement described above may be insufficient to generate the measured top quarkTop quark
The top quark, also known as the t quark or truth quark, is an elementary particle and a fundamental constituent of matter. Like all quarks, the top quark is an elementary fermion with spin-, and experiences all four fundamental interactions: gravitation, electromagnetism, weak interactions, and...
mass, even for an ETC scale as low as a few TeV. However, this problem could be addressed if the effective four-technifermion coupling resulting from ETC gauge boson exchange is strong and tuned just above a critical value. The analysis of this strong-ETC possibility is that of a Nambu–Jona–Lasinio model with an additional (technicolor) gauge interaction. The technifermion masses are small compared to the ETC scale (the cutoff on the effective theory), but nearly constant out to this scale, leading to a large top quark mass. No fully realistic ETC theory for all quark masses has yet been developed incorporating these ideas. A related study was carried out by Miransky and Yamawaki. A problem with this approach is that it involves some degree of parameter fine-tuning
Fine-tuning
In theoretical physics, fine-tuning refers to circumstances when the parameters of a model must be adjusted very precisely in order to agree with observations. Theories requiring fine-tuning are regarded as problematic in the absence of a known mechanism to explain why the parameters happen to...
, in conflict with technicolor’s guiding principle of naturalness.
Finally, it should be noted that there is a large body of closely related work in which ETC does not generate mt. These are the top quark condensate
Top quark condensate
In particle physics, the top quark condensate theory is an alternative to the Standard Model in which a fundamental scalar Higgs field is replaced by a composite field composed of the top quark and its antiquark. These are bound by a four-fermion interaction, analogous to Cooper pairs in a BCS...
, topcolor
Topcolor
In theoretical physics, Topcolor is a model of dynamical electroweak symmetry breaking in which the top quark and anti-top quark form a top quark condensate and act effectively like the Higgs boson. This is analogous to the phenomenon of superconductivity....
and top-color-assisted technicolor models, in which new strong interactions are ascribed to the top quark and other third-generation fermions. As with the strong-ETC scenario described above, all these proposals involve a considerable degree of fine-tuning of gauge couplings.
Minimal Walking Models
In 2004 Francesco SanninoFrancesco Sannino
Francesco Sannino is an Italian theoretical physicist and a professor at the University of Southern Denmark. He is an expert in effective field theories and their applications to strongly coupled theories such as quantum chromodynamics. He is also an expert in beyond standard model physics and...
and Kimmo Tuominen proposed technicolor models with technifermions in higher-dimensional representations of the technicolor gauge group. They argued that these more "minimal" models required fewer flavors of technifermions in order to exhibit walking behavior, making it easier to pass precision electroweak tests.
For example, SU(2) and SU(3) gauge theories may exhibit walking with as few as two Dirac flavors of fermions in the adjoint or two-index symmetric representation. In contrast, at least eight flavors of fermions in the fundamental representation of SU(3) (and possibly SU(2) as well) are required to reach the near-conformal regime.
These results continue to be investigated by various methods, including lattice simulations discussed below, which have confirmed the near-conformal dynamics of these minimal walking models. The first comprehensive effective Lagrangian for minimal walking models, featuring a light composite Higgs, spin-one states, tree-level unitarity
Unitarity (physics)
In quantum physics, unitarity is a restriction on the allowed evolution of quantum systems that insures the sum of probabilities of all possible outcomes of any event is always 1....
, and consistency with phenomenological constraints was constructed in 2007 by Foadi, Frandsen, Ryttov and Sannino.
Technicolor on the lattice
Lattice gauge theoryLattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
is a non-perturbative method applicable to strongly-interacting technicolor theories, allowing first-principles exploration of walking and conformal dynamics. In 2007, Catterall and Sannino used lattice gauge theory to study SU(2) gauge theories with two flavors of Dirac fermions in the symmetric representation, finding evidence of conformality that has been confirmed by subsequent studies.
As of 2010, the situation for SU(3) gauge theory with fermions in the fundamental representation is not as clear-cut. In 2007, Appelquist, Fleming and Neil reported evidence that a non-trivial infrared fixed point develops in such theories when there are twelve flavors, but not when there are eight. While some subsequent studies confirmed these results, others reported different conclusions, depending on the lattice methods used, and there is not yet consensus.
Further lattice studies exploring these issues, as well as considering the consequences of these theories for precision electroweak measurements
Peskin-Takeuchi parameter
In particle physics, the Peskin–Takeuchi parameters are a set of three measurable quantities, called S, T, and U, that parameterize potential new physics contributions to electroweak radiative corrections...
, are underway by several research groups.
Technicolor phenomenology
Any framework for physics beyond the Standard ModelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
must conform with precision measurements of the electroweak parameters. Its consequences for physics at existing and future high-energy hadron colliders, and for the dark matter of the universe must also be explored.
Precision electroweak tests
In 1990, the phenomenological parameters S, T, and UPeskin-Takeuchi parameter
In particle physics, the Peskin–Takeuchi parameters are a set of three measurable quantities, called S, T, and U, that parameterize potential new physics contributions to electroweak radiative corrections...
were introduced by Peskin and Takeuchi to quantify contributions to electroweak radiative corrections from physics beyond the Standard Model. They have a simple relation to the parameters of the electroweak chiral Lagrangian. The Peskin-Takeuchi analysis was based on the general formalism for weak radiative corrections developed by Kennedy, Lynn, Peskin and Stuart, and alternate formulations also exist.
The S, T, and U-parameters describe corrections to the electroweak gauge boson propagators from physics Beyond the Standard Model
Beyond the Standard Model
Physics beyond the Standard Model refers to the theoretical developments needed to explain the deficiencies of the Standard Model, such as the origin of mass, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy...
. They can be written in terms of polarization functions of electroweak currents and their spectral representation as follows:
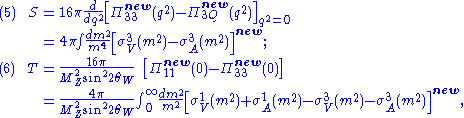
where only new, beyond-standard-model physics is included. The quantities are calculated relative to a minimal Standard Model with some chosen reference mass of the Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
, taken to range from the experimental lower bound of 117 GeV to 1000 GeV where its width becomes very large. For these parameters to describe the dominant corrections to the Standard Model, the mass scale of the new physics must be much greater than MW and MZ, and the coupling of quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s and lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s to the new particles must be suppressed relative to their coupling to the gauge bosons. This is the case with technicolor, so long as the lightest technivector mesons, ρT and aT, are heavier than 200–300 GeV. The S-parameter is sensitive to all new physics at the TeV scale, while T is a measure of weak-isospin breaking effects. The U-parameter is generally not useful; most new-physics theories, including technicolor theories, give negligible contributions to it.
The S and T-parameters are determined by global fit to experimental data including Z-pole data from LEP
Large Electron-Positron Collider
The Large Electron–Positron Collider was one of the largest particle accelerators ever constructed.It was built at CERN, a multi-national centre for research in nuclear and particle physics near Geneva, Switzerland. LEP was a circular collider with a circumference of 27 kilometres built in a...
at CERN
CERN
The European Organization for Nuclear Research , known as CERN , is an international organization whose purpose is to operate the world's largest particle physics laboratory, which is situated in the northwest suburbs of Geneva on the Franco–Swiss border...
, top quark and W-mass measurements at Fermilab, and measured levels of atomic parity violation. The resultant bounds on these parameters are given in the Review of Particle Properties. Assuming U = 0, the S and T parameters are small and, in fact, consistent with zero:
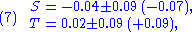
where the central value corresponds to a Higgs mass of 117 GeV and the correction to the central value when the Higgs mass is increased to 300 GeV is given in parentheses. These values place tight restrictions on beyond-standard-model theories—when the relevant corrections can be reliably computed.
The S parameter estimated in QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
-like technicolor theories is significantly greater than the experimentally-allowed value. The computation was done assuming that the spectral integral for S is dominated by the lightest ρT and aT resonances, or by scaling effective Lagrangian parameters from QCD. In walking technicolor, however, the physics at the TeV scale and beyond must be quite different from that of QCD-like theories. In particular, the vector and axial-vector spectral functions cannot be dominated by just the lowest-lying resonances. It is unknown whether higher energy contributions to
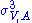are a tower of identifiable ρT and aT states or a smooth continuum. It has been conjectured that ρT and aT partners could be more nearly degenerate in walking theories (approximate parity doubling), reducing their contribution to S. LatticeLattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
calculations are underway or planned to test these ideas and obtain reliable estimates of S in walking theories.
The restriction on the T-parameter poses a problem for the generation of the top-quark mass in the ETC framework. The enhancement from walking can allow the associated ETC scale to be as large as a few TeV, but—since the ETC interactions must be strongly weak-isospin breaking to allow for the large top-bottom mass splitting—the contribution to the T parameter, as well as the rate for the decay
, could be too large.Hadron collider phenomenology
Early studies generally assumed the existence of just one electroweakElectroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
doublet of technifermions, or one techni-family including one doublet each of color-triplet techniquarks and color-singlet technileptons. In the minimal, one-doublet model, three Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
s (technipions, πT) have decay constant F = FEW = 246 GeV and are eaten by the electroweak gauge bosons. The most accessible collider signal is the production through
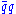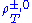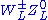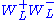annihilation in a hadron collider of spin-one , and their subsequent decay into a pair of longitudinally-polarized weak bosons, and . At an expected mass of 1.5–2.0 TeV and width of 300–400 GeV, such ρT's would be difficult to discover at the LHC. A one-family model has a large number of physical technipions, with F = FEW/ = 123 GeV. There is a collection of correspondingly lower-mass color-singlet and octet technivectors decaying into technipion pairs. The πT's are expected to decay to the heaviest possible quark and lepton pairs. Despite their lower masses, the ρT's are wider than in the minimal model and the backgrounds to the πT decays are likely to be insurmountable at a hadron collider.This picture changed with the advent of walking technicolor. A walking gauge coupling occurs if αχ SB lies just below the IR fixed point value αIR, which requires either a large number of electroweak doublets in the fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
of the gauge group, e.g., or a few doublets in higher-dimensional TC representations. In the latter case, the constraints on ETC representations generally imply other technifermions in the fundamental representation as well. In either case, there are technipions πT with decay constant
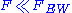. This implies so that the lightest technivectors accessible at the LHC—ρT, ωT, aT (with IG JPC = 1+ 1−−, 0− 1−−, 1− 1++)—have masses well below a TeV. The class of theories with many technifermions and thus 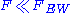is called low-scale technicolor.A second consequence of walking technicolor concerns the decays of the spin-one technihadrons. Since technipion masses
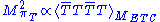(see Eq. (4)), walking enhances them much more than it does other technihadron masses. Thus, it is very likely that the lightest MρT < 2MπT and that the two and three-πT decay channels of the light technivectors are closed. This further implies that these technivectors are very narrow. Their most probable two-body channels are 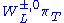, WL WL, γ πT and γ WL. The coupling of the lightest technivectors to WL is proportional to F/FEW. Thus, all their decay rates are suppressed by powers of 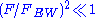or the fine-structure constant, giving total widths of a few GeV (for ρT) to a few tenths of a GeV (for ωT and T).A more speculative consequence of walking technicolor is motivated by consideration of its contribution to the S-parameter. As noted above, the usual assumptions made to estimate STC are invalid in a walking theory. In particular, the spectral integrals used to evaluate STC cannot be dominated by just the lowest-lying ρT and aT and, if STC is to be small, the masses and weak-current couplings of the ρT and aT could be more nearly equal than they are in QCD.
Low-scale technicolor phenomenology, including the possibility of a more parity-doubled spectrum, has been developed into a set of rules and decay amplitudes. An April 2011 announcement of an excess in jet pairs produced in association with a W boson measured at the Tevatron
Tevatron
The Tevatron is a circular particle accelerator in the United States, at the Fermi National Accelerator Laboratory , just east of Batavia, Illinois, and is the second highest energy particle collider in the world after the Large Hadron Collider...
has been interpreted by Eichten, Lane and Martin as a possible signal of the technipion of low-scale technicolor.
The general scheme of low-scale technicolor makes little sense if the limit on
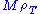is pushed past about 700 GeV. The LHC should be able to discover it or rule it out. Searches there involving decays to technipions and thence to heavy quark jets are hampered by backgrounds from production; its rate is 100 times larger than that at the Tevatron. 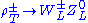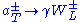Consequently, the discovery of low-scale technicolor at the LHC relies on all-leptonic final-state channels with favorable signal-to-background ratios: , and 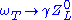.Dark matter
Technicolor theories naturally contain dark matterDark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
candidates. Almost certainly, models can be built in which the lowest-lying technibaryon, a technicolor-singlet bound state of technifermions, is stable enough to survive the evolution of the universe. If the technicolor theory is low-scale (
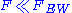), the baryon's mass should be no more than 1–2 TeV. If not, it could be much heavier. The technibaryon must be electrically neutral and satisfy constraints on its abundance. Given the limits on spin-independent dark-matter-nucleon cross sections from dark-matter search experiments ( 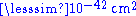for the masses of interest), it may have to be electroweak neutral (weak isospin I = 0) as well. These considerations suggest that the "old" technicolor dark matter candidates may be difficult to produce at the LHC.A different class of technicolor dark matter candidates light enough to be accessible at the LHC was introduced by Francesco Sannino
Francesco Sannino
Francesco Sannino is an Italian theoretical physicist and a professor at the University of Southern Denmark. He is an expert in effective field theories and their applications to strongly coupled theories such as quantum chromodynamics. He is also an expert in beyond standard model physics and...
and his collaborators. These states are pseudo Goldstone bosons possessing a global charge that makes them stable against decay.