Theoretical motivation for general relativity
Encyclopedia
A Theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity
by examining the dynamics
of particles in circular orbit
s about the earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori
. This provides a means to inform and verify the formalism.
General relativity
addresses two questions:
The former question is answered with the geodesic equation. The second question is answered with the Einstein field equation. The geodesic equation and the field equation are related through a principle of least action
. The motivation for the geodesic equation is provided in the section #Geodesic equation for circular orbits The motivation for the Einstein field equation is provided in the section #Stress-energy tensor
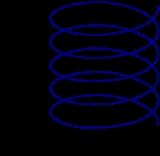
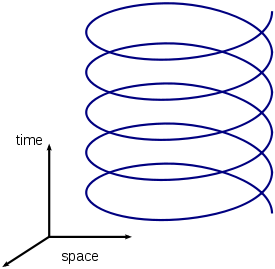For definiteness consider a circular earth orbit (helical world line
) of a particle. The particle travels with speed v. An observer on earth sees that length is contracted in the frame of the particle. A measuring stick traveling with the particle appears shorter to the earth observer. Therefore the circumference of the orbit, which is in the direction of motion appears longer than
times the diameter of the orbit.
In special relativity
the 4-velocity of the particle in the inertial (non-accelerating) frame of the earth is
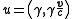
where c is the speed of light
,
is the 3-velocity, and 
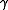is
.
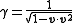The magnitude of the 4-velocity vector is always constant
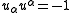
where we are using a Minkowski metric
.
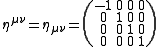The magnitude of the 4-velocity is therefore a Lorentz scalar
.
The 4-acceleration in the earth (non-accelerating) frame is
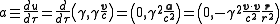
where
is c times the proper time interval measured in the frame of the particle. This is related to the time interval in the Earth's frame by
.
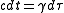Here, the 3-acceleration for a circular orbit is
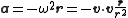
where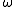
is the angular velocity of the rotating particle and 
is the 3-position of the particle.
The magnitude of the 4-velocity is constant. This implies that the 4-acceleration must be perpendicular to the 4-velocity. The 4-acceleration is, in fact, perpendicular to the 4-velocity in this example (see Fermi-Walker transport
). The inner product of the 4-acceleration and the 4-velocity is therefore always zero. The inner product is a Lorentz scalar
.
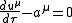
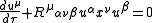
where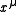
is the 4-position of the particle and 
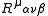is the curvature
tensor give by
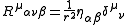
where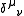
is the Kronecker delta function, and we have the constraints
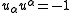
and
.
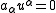It is easily verified that circular orbits satisfy the geodesic equation. The geodesic equation is actually more general. Circular orbits are a particular solution of the equation. Solutions other than circular orbits are permissible and valid.
tensor is a special curvature tensor given by the contraction
.
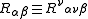The trace of the Ricci tensor, called the scalar curvature
, is
.
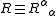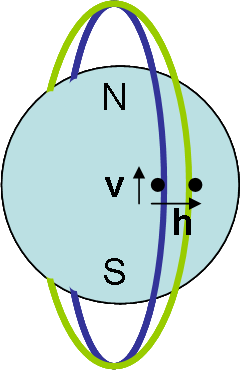Consider the situation in which there are now two particles in nearby circular
polar
orbits of the earth
at radius
and speed 
.
The particles execute simple harmonic motion
about the earth and with respect to each other. They are at their maximum distance from each other as they cross the equator. Their trajectories
intersect at the poles.
Imagine we have a spacecraft co-moving with one of the particles. The ceiling of the craft, the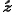
direction, coincides with the 
direction. The front of the craft is in the 
direction, and the 
direction is to the left of the craft. The spacecraft is small compared with the size of the orbit so that the local frame is a local Lorentz frame. The 4-separation of the two particles is given by 
. In the local frame of the spacecraft the geodesic equation is given by
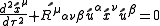
where
and
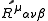
is the curvature tensor in the local frame.
.
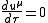If we require a particle to travel along a geodesic in curved spacetime, then the analogous expression in curved spacetime is
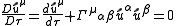
where the derivative on the left is the covariant derivative
, which is the generalization of the normal derivative to a derivative in curved spacetime. Here
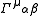
is a Christoffel symbol.
The curvature is related to the Christoffel symbol by
.
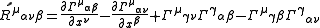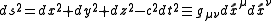
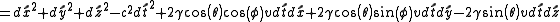
where
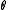is the angle with the z axis (longitude) and
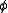is the angle with the x axis (latitude).
This gives a metric
of
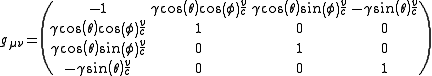
in the local frame.
The inverse of the metric tensor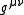
is defined such that
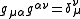
where the term on the right is the Kronecker delta.
The transformation of the infinitesimal 4-volume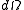
is
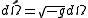
where g is the determinant of the metric tensor.
The differential of the determinant of the metric tensor is
.
The relationship between the Christoffel symbols and the metric tensor is
.
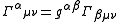
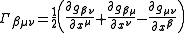between two events in spacetime is that world line that minimizes the action between the two events. In classical mechanics
the principle of least action is used to derive Newton's laws of motion
and is the basis for Lagrangian dynamics. In relativity it is expressed as
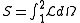
between events 1 and 2 is a minimum. Here S is a scalar
and
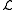
is known as the Lagrangian density. The Lagrangian density is divided into two parts, the density for the orbiting particle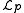
and the density 
of the gravitational field generated by all other particles including those comprising the earth,
.
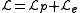In curved spacetime
, the "shortest" world line is that geodesic
that minimizes the curvature along the geodesic. The action then is proportional to the curvature of the world line. Since S is a scalar, the scalar curvature
is the appropriate measure of curvature. The action for the particle is therefore
where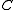
is an unknown constant. This constant will be determined by requiring the theory to reduce to Newton's law of gravitation in the nonrelativistic limit.
The Lagrangian density for the particle is therefore
.
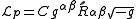The action for the particle and the earth is
.
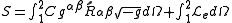We find the world line that lies on the surface of the sphere of radius r by varying the metric tensor. Minimization and neglect of terms that disappear on the boundaries, including terms second order in the derivative of g, yields
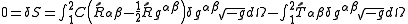
where
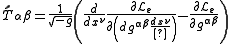
is the Hilbert stress-energy tensor
of the field generated by the earth.
The relationship, to within an unknown constant factor, between the stress-energy and the curvature is
.
Newton's Law of Gravitation in non-relativistic mechanics states that the acceleration on an object of mass
due to another object of mass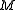 
is equal to
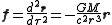
where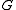
is the gravitational constant
,
is a vector from mass 
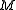to mass 
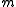and 
is the magnitude of that vector. The time t is scaled with the speed of light
c
.
The acceleration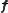
is independent of 
.
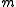For definiteness. consider a particle of mass
orbiting in the gravitational field of the earth with mass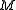 
. The law of gravitation can be written
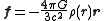
where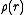
is the average mass density inside a sphere
of radius
.
.
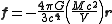where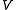
is the volume
of a sphere of radius
. The quantity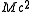 
will be recognized from special relativity
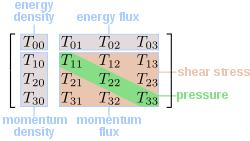
as the rest energy of the large body, the earth. This is the sum of the rest energies of all the particles that compose earth. The quantity in the parentheses is then the average rest energy density of a sphere of radius
about the earth. The gravitational field is proportional to the average energy density within a radius r. This is the 00 component of the stress-energy tensor
in relativity
for the special case in which all the energy is rest energy. More generally
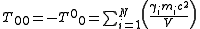
where
and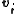
is the velocity of particle i making up the earth and 
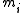in the rest mass of particle i. There are N particles altogether making up the earth.
There are two simple relativistic entities that reduce to the 00 component of the stress-energy tensor in the nonrelativistic limit
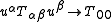
and the trace
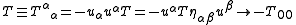
where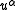
is the 4-velocity.
The 00 component of the stress-energy tensor can be generalized to the relativistic case as a linear combination of the two terms
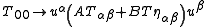
where
.
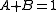
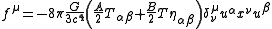Unfortunately, this acceleration is nonzero for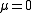
as is required for circular orbits. Since the magnitude of the 4-velocity is constant, it is only the component of the force perpendicular to the 4-velocity that contributes to the acceleration. We must therefore subtract off the component of force parallel to the 4-velocity. This is known as Fermi-Walker transport
. In other words
.
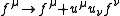This yields
.
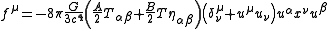The force in the local frame is
.
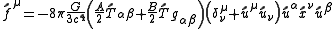We obtain the Einstein field equation by equating the acceleration required for circular orbits with the acceleration due to gravity
.
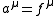
This is the relationship between curvature of spacetime and the stress-energy tensor.
The Ricci tensor becomes
.
The trace of the Ricci tensor is
.
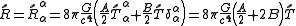Comparison of the Ricci tensor with the Ricci tensor calculated from the principle of least action, Theoretical motivation for general relativity#Principle of least action in general relativity identifying the stress-energy tensor with the Hilbert stress-energy, and remembering that A+B=1 removes the ambiguity in A, B, and C.
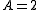
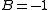
and
.
This gives
.
The field equation can be written
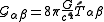
where
.
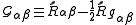This is the Einstein field equation that describes curvature of spacetime that results from stress-energy density. This equation, along with the geodesic equation have motivated by the kinetics and dynamics of a particle orbiting the earth in a circular orbit. They are true in general.
.
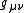Typically there is an initial guess for the tensor. The guess is used to calculate Christoffel symbols, which are used to calculate the curvature. If the Einstein field equation is not satisfied, the process is repeated.
Solutions occur in two forms, vacuum solutions and non-vacuum solutions. A vacuum solution
is one in which the stress-energy tensor is zero. The relevant vacuum solution for circular orbits is the Schwarzschild metric
. There are also a number of exact solutions
that are non-vacuum solutions, solutions in which the stress tensor is non-zero.
, the equations of electrodynamics, in curved spacetime are a generalization of Maxwell's equations in flat spacetime
(see Formulation of Maxwell's equations in special relativity
). Curvature of spacetime affects electrodynamics. Maxwell's equations in curved spacetime can be obtained by replacing the derivatives in the equations in flat spacetime with covariant derivative
s. The sourced and source-free equations become (cgs units):
,
and
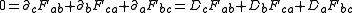
where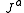
is the 4-current, 
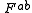is the field strength tensor
,
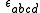is the Levi-Civita symbol
, and
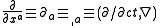
is the 4-gradient
. Repeated indices are summed over according to Einstein summation convention
. We have displayed the results in several common notations.
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss' law and the Ampère's law with Maxwell's correction. The second equation is an expression of the homogenous equations, Faraday's law of induction
and Gauss's law for magnetism.
The electromagnetic wave equation is modified from the equation in flat spacetime in two ways, the derivative is replaced with the covariant derivative and a new term that depends on the curvature appears.
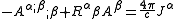
where the 4-potential is defined such that
.
We have assumed the generalization of the Lorenz gauge in curved spacetime
.
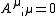Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
by examining the dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
of particles in circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s about the earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori
A priori and a posteriori (philosophy)
The terms a priori and a posteriori are used in philosophy to distinguish two types of knowledge, justifications or arguments...
. This provides a means to inform and verify the formalism.
General relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
addresses two questions:
- How does the curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
affect the motion of matterMatterMatter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
? - How does the presence of matter affect the curvature of spacetime?
The former question is answered with the geodesic equation. The second question is answered with the Einstein field equation. The geodesic equation and the field equation are related through a principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
. The motivation for the geodesic equation is provided in the section #Geodesic equation for circular orbits The motivation for the Einstein field equation is provided in the section #Stress-energy tensor
Geodesic equation for circular orbits
Kinetics of circular orbits
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
) of a particle. The particle travels with speed v. An observer on earth sees that length is contracted in the frame of the particle. A measuring stick traveling with the particle appears shorter to the earth observer. Therefore the circumference of the orbit, which is in the direction of motion appears longer than
times the diameter of the orbit.In special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
the 4-velocity of the particle in the inertial (non-accelerating) frame of the earth is
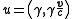
where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
,
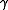is the 3-velocity, and is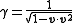.The magnitude of the 4-velocity vector is always constant
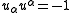
where we are using a Minkowski metric
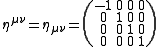.The magnitude of the 4-velocity is therefore a Lorentz scalar
Lorentz scalar
In physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors...
.
The 4-acceleration in the earth (non-accelerating) frame is
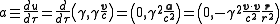
where
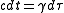is c times the proper time interval measured in the frame of the particle. This is related to the time interval in the Earth's frame by.Here, the 3-acceleration for a circular orbit is
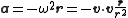
where
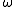is the angular velocity of the rotating particle and is the 3-position of the particle.The magnitude of the 4-velocity is constant. This implies that the 4-acceleration must be perpendicular to the 4-velocity. The 4-acceleration is, in fact, perpendicular to the 4-velocity in this example (see Fermi-Walker transport
Fermi-Walker transport
Fermi-Walker transport is a process in general relativity used to define a coordinate system or reference frame such that all curvature in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame....
). The inner product of the 4-acceleration and the 4-velocity is therefore always zero. The inner product is a Lorentz scalar
Lorentz scalar
In physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors...
.
Curvature of spacetime: Geodesic equation
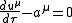
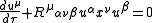
The equation for the acceleration can be generalized, yielding the geodesic equationwhere
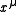is the 4-position of the particle and 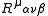is the curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
tensor give by
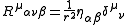
where
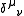is the Kronecker delta function, and we have the constraints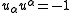and
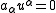.It is easily verified that circular orbits satisfy the geodesic equation. The geodesic equation is actually more general. Circular orbits are a particular solution of the equation. Solutions other than circular orbits are permissible and valid.
Ricci curvature tensor and trace
The Ricci curvatureRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
tensor is a special curvature tensor given by the contraction
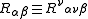.The trace of the Ricci tensor, called the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
, is
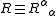.The geodesic equation in a local coordinate system
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
polar
Polar orbit
A polar orbit is an orbit in which a satellite passes above or nearly above both poles of the body being orbited on each revolution. It therefore has an inclination of 90 degrees to the equator...
orbits of the earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
at radius
and speed .The particles execute simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
about the earth and with respect to each other. They are at their maximum distance from each other as they cross the equator. Their trajectories
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
intersect at the poles.
Imagine we have a spacecraft co-moving with one of the particles. The ceiling of the craft, the
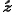direction, coincides with the direction. The front of the craft is in the direction, and the direction is to the left of the craft. The spacecraft is small compared with the size of the orbit so that the local frame is a local Lorentz frame. The 4-separation of the two particles is given by . In the local frame of the spacecraft the geodesic equation is given by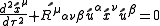where
and
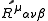
is the curvature tensor in the local frame.
Geodesic equation as a covariant derivative
The equation of motion for a particle in flat spacetime and in the absence of forces is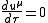.If we require a particle to travel along a geodesic in curved spacetime, then the analogous expression in curved spacetime is
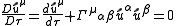
where the derivative on the left is the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
, which is the generalization of the normal derivative to a derivative in curved spacetime. Here
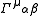
is a Christoffel symbol.
The curvature is related to the Christoffel symbol by
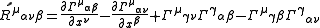.Metric tensor in the local frame
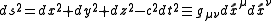
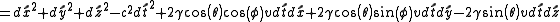
The interval in the local frame iswhere
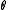is the angle with the z axis (longitude) and 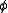is the angle with the x axis (latitude).This gives a metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
of
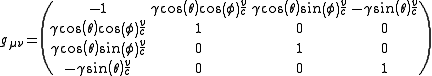
in the local frame.
The inverse of the metric tensor
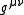is defined such that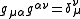where the term on the right is the Kronecker delta.
The transformation of the infinitesimal 4-volume
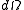is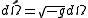where g is the determinant of the metric tensor.
The differential of the determinant of the metric tensor is
.The relationship between the Christoffel symbols and the metric tensor is
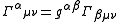
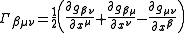.Principle of least action in general relativity
The principle of least action states that the world lineWorld line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
between two events in spacetime is that world line that minimizes the action between the two events. In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
the principle of least action is used to derive Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
and is the basis for Lagrangian dynamics. In relativity it is expressed as
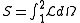
between events 1 and 2 is a minimum. Here S is a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
and
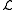
is known as the Lagrangian density. The Lagrangian density is divided into two parts, the density for the orbiting particle
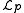and the density of the gravitational field generated by all other particles including those comprising the earth,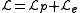.In curved spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, the "shortest" world line is that geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
that minimizes the curvature along the geodesic. The action then is proportional to the curvature of the world line. Since S is a scalar, the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
is the appropriate measure of curvature. The action for the particle is therefore
where
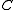is an unknown constant. This constant will be determined by requiring the theory to reduce to Newton's law of gravitation in the nonrelativistic limit.The Lagrangian density for the particle is therefore
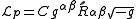.The action for the particle and the earth is
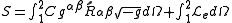.We find the world line that lies on the surface of the sphere of radius r by varying the metric tensor. Minimization and neglect of terms that disappear on the boundaries, including terms second order in the derivative of g, yields
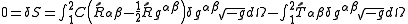
where
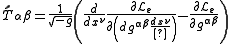
is the Hilbert stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
of the field generated by the earth.
The relationship, to within an unknown constant factor, between the stress-energy and the curvature is
.Newton's law of gravitation
Newton's Law of Gravitation in non-relativistic mechanics states that the acceleration on an object of mass
due to another object of mass 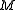is equal to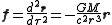where
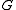is the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
,
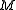is a vector from mass to mass 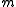and is the magnitude of that vector. The time t is scaled with the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c
.The acceleration
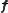is independent of 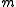.For definiteness. consider a particle of mass
orbiting in the gravitational field of the earth with mass 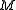. The law of gravitation can be written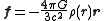where
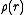is the average mass density inside a sphereVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of radius
.Gravitational force in terms of the 00 component of the stress-energy tensor
Newton's law can be written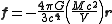.where
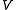is the volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a sphere of radius
. The quantity 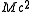will be recognized from special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
as the rest energy of the large body, the earth. This is the sum of the rest energies of all the particles that compose earth. The quantity in the parentheses is then the average rest energy density of a sphere of radius
about the earth. The gravitational field is proportional to the average energy density within a radius r. This is the 00 component of the stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
in relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
for the special case in which all the energy is rest energy. More generally
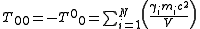
where
and
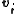is the velocity of particle i making up the earth and 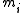in the rest mass of particle i. There are N particles altogether making up the earth.Relativistic generalization of the energy density
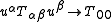
and the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
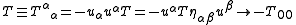
where
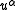is the 4-velocity.The 00 component of the stress-energy tensor can be generalized to the relativistic case as a linear combination of the two terms
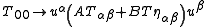
where
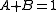
4-acceleration due to gravity
The 4-acceleration due to gravity can be written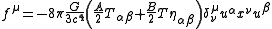.Unfortunately, this acceleration is nonzero for
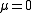as is required for circular orbits. Since the magnitude of the 4-velocity is constant, it is only the component of the force perpendicular to the 4-velocity that contributes to the acceleration. We must therefore subtract off the component of force parallel to the 4-velocity. This is known as Fermi-Walker transportFermi-Walker transport
Fermi-Walker transport is a process in general relativity used to define a coordinate system or reference frame such that all curvature in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame....
. In other words
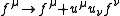.This yields
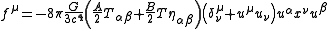.The force in the local frame is
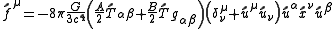.Einstein field equation
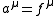
.This is the relationship between curvature of spacetime and the stress-energy tensor.
The Ricci tensor becomes
.The trace of the Ricci tensor is
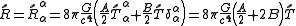.Comparison of the Ricci tensor with the Ricci tensor calculated from the principle of least action, Theoretical motivation for general relativity#Principle of least action in general relativity identifying the stress-energy tensor with the Hilbert stress-energy, and remembering that A+B=1 removes the ambiguity in A, B, and C.
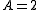
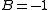
and
.This gives
.The field equation can be written
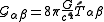
where
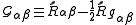.This is the Einstein field equation that describes curvature of spacetime that results from stress-energy density. This equation, along with the geodesic equation have motivated by the kinetics and dynamics of a particle orbiting the earth in a circular orbit. They are true in general.
Solving the Einstein field equation
Solving the Einstein field equation requires an iterative process. The solution is represented in the metric tensor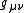.Typically there is an initial guess for the tensor. The guess is used to calculate Christoffel symbols, which are used to calculate the curvature. If the Einstein field equation is not satisfied, the process is repeated.
Solutions occur in two forms, vacuum solutions and non-vacuum solutions. A vacuum solution
Vacuum solution (general relativity)
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor also vanishes identically, so that no matter or non-gravitational fields are present.More generally, a...
is one in which the stress-energy tensor is zero. The relevant vacuum solution for circular orbits is the Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
. There are also a number of exact solutions
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
that are non-vacuum solutions, solutions in which the stress tensor is non-zero.
Solving the geodesic equation
Solving the geodesic equations requires knowledge of the metric tensor obtained through the solution of the Einstein field equation. Either the Christoffel symbols or the curvature are calculated from the metric tensor. The geodesic equation is then integrated with the appropriate boundary conditions.Electrodynamics in curved spacetime
Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, the equations of electrodynamics, in curved spacetime are a generalization of Maxwell's equations in flat spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
(see Formulation of Maxwell's equations in special relativity
Formulation of Maxwell's equations in special relativity
The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form which is "manifestly covariant" , in the formalism of special relativity...
). Curvature of spacetime affects electrodynamics. Maxwell's equations in curved spacetime can be obtained by replacing the derivatives in the equations in flat spacetime with covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s. The sourced and source-free equations become (cgs units):
,and
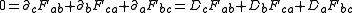
where
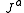is the 4-current, 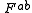is the field strength tensorElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
,
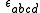is the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
, and
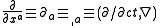
is the 4-gradient
Four-gradient
The four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...
. Repeated indices are summed over according to Einstein summation convention
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
. We have displayed the results in several common notations.
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss' law and the Ampère's law with Maxwell's correction. The second equation is an expression of the homogenous equations, Faraday's law of induction
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
and Gauss's law for magnetism.
The electromagnetic wave equation is modified from the equation in flat spacetime in two ways, the derivative is replaced with the covariant derivative and a new term that depends on the curvature appears.
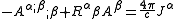
where the 4-potential is defined such that
.We have assumed the generalization of the Lorenz gauge in curved spacetime
.
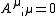