
Topological entropy (in physics)
Encyclopedia
The topological entanglement entropy, usually denoted by γ, is a number characterizing many-body states that possess topological order
.
The short form topological entropy is often used, although the same name in ergodic theory
refers to an unrelated mathematical concept (see topological entropy
).
A non-zero topological entanglement entropy reflects the presence of long range quantum entanglements in a many-body quantum state. So the topological entanglement entropy links topological order
with pattern of
long range quantum entanglements.
Given a topologically ordered
state, the topological entropy can be extracted from the asymptotic behavior of the Von Neumann entropy
measuring the quantum entanglement
between a spatial block and the rest of the system. The entanglement entropy of a simply connected region of boundary length L, within an infinite two-dimensional topologically ordered state, has the following form for large L:
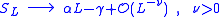
-γ is the topological entanglement entropy.
The topological entanglement entropy is equal to the logarithm of the total quantum dimension of the quasiparticle excitations of the state.
For example, the simplest fractional quantum Hall states, the Laughlin states at filling fraction 1/m, have γ = ½log(m). The Z2 fractionalized states, such as topologically ordered states of
Z2 spin-liquid, quantum dimer models
on non-bipartite lattices, and Kitaev's toric code
state, are characterized γ = log(2).
Topological order
In physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
.
The short form topological entropy is often used, although the same name in ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
refers to an unrelated mathematical concept (see topological entropy
Topological entropy
In mathematics, the topological entropy of a topological dynamical system is a nonnegative real number that measures the complexity of the system. Topological entropy was first introduced in 1965 by Adler, Konheim and McAndrew. Their definition was modelled after the definition of the...
).
A non-zero topological entanglement entropy reflects the presence of long range quantum entanglements in a many-body quantum state. So the topological entanglement entropy links topological order
Topological order
In physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
with pattern of
long range quantum entanglements.
Given a topologically ordered
Topological order
In physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
state, the topological entropy can be extracted from the asymptotic behavior of the Von Neumann entropy
Von Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
measuring the quantum entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
between a spatial block and the rest of the system. The entanglement entropy of a simply connected region of boundary length L, within an infinite two-dimensional topologically ordered state, has the following form for large L:
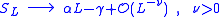
-γ is the topological entanglement entropy.
The topological entanglement entropy is equal to the logarithm of the total quantum dimension of the quasiparticle excitations of the state.
For example, the simplest fractional quantum Hall states, the Laughlin states at filling fraction 1/m, have γ = ½log(m). The Z2 fractionalized states, such as topologically ordered states of
Z2 spin-liquid, quantum dimer models
Quantum dimer models
Quantum dimer models were introduced to model the physics of resonating valence bond states in lattice spin systems. The only degrees of freedom retained from the motivating spin systems are the valence bonds, represented as dimers which live on the lattice bonds...
on non-bipartite lattices, and Kitaev's toric code
Toric code
The Toric Code is a topological quantum error correcting code, and an example of a stabilizer code, defined on a two dimensional spin lattice It is the simplest and most well studied of the quantum double models...
state, are characterized γ = log(2).
See also
- Quantum topologyQuantum topologyQuantum topology is a branch of mathematics that connects quantum mechanics with low-dimensional topology.Dirac notation provides a viewpoint of quantum mechanics which becomes amplified into a framework that can embrace the amplitudes associated with topological spaces and the related embedding of...
- Topological defectTopological defectIn mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
- Topological orderTopological orderIn physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
- Topological quantum field theoryTopological quantum field theoryA topological quantum field theory is a quantum field theory which computes topological invariants....
- Topological quantum numberTopological quantum numberIn physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...
- Topological string theoryTopological string theoryIn theoretical physics, topological string theory is a simplified version of string theory. The operators in topological string theory represent the algebra of operators in the full string theory that preserve a certain amount of supersymmetry...
Introduction of the quantity
- Topological Entanglement Entropy, Alexei Kitaev and John Preskill, Phys. Rev. Lett. 96, 110404 (2006).
- Detecting Topological Order in a Ground State Wave Function, Michael Levin and Xiao-Gang Wen, Phys. Rev. Lett. 96, 110405 (2006).
Calculations for specific topologically ordered states
- M. Haque, O. Zozulya and K. Schoutens; Phys. Rev. Lett. 98, 060401 (2007).
- S. Furukawa and G. Misguich, Phys. Rev. B 75, 214407 (2007).

