Weil pairing
Encyclopedia
In mathematics
, the Weil pairing is a construction of roots of unity by means of functions on an elliptic curve
E, in such a way as to constitute a pairing
(bilinear form, though with multiplicative notation) on the torsion subgroup
of E. The name is for André Weil
, who gave an abstract algebraic definition; the corresponding results for elliptic function
s were known, and can be expressed simply by use of the Weierstrass sigma function
.
K. Given an integer n > 0 (we require n to be prime to char(K) if char(K)> 0) such that K contains a primitive nth root of unity, then the n-torsion on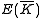
has known structure, as a Cartesian product
of two cyclic group
s of order n. The basis of the construction is of an n-th root of unity
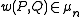
for given points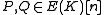
, where 
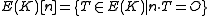and 
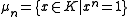, by means of Kummer theory
.
By a direct argument one can define a function F in the function field
of E over the algebraic closure
of K, by its divisor
:
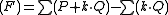
with sums for 0 ≤ k < n. In words F has a simple zero at each point P + kQ, and a simple pole at each point kQ. Then F is well-defined up to multiplication by a constant. If G is the translation of F by Q, then by construction G has the same divisor. One can show that
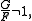
unless P and Q generate cyclic subgroups one of which is inside the other. In fact then G/F would yield a function on the isogenous curve E/C where C is the cyclic subgroup generated by Q, having just one simple pole. Such a function cannot exist, as follows by proving the residue at the pole is zero, a contradiction.
Therefore if we define
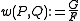
we shall have an n-th root of unity (translating n times must give 1) other than 1. With this definition it can be shown that w is antisymmetric and bilinear, giving rise to a non-degenerate pairing on the n-torsion.
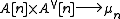
for all n prime to the characteristic of k. Here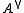
denotes the dual abelian variety
of A. This is the so-called Weil pairing for higher dimensions. If A is equipped with a polarisation
,
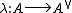then composition gives a (possibly degenerate) pairing
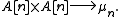
If C is a projective, nonsingular curve of genus ≥ 0 over k, and J its Jacobian
, then the theta-divisor
of J induces a principal polarisation of J, which in this particular case happens to be an isomorphism (see autoduality of Jacobians). Hence, composing the Weil pairing for J with the polarisation gives a nondegenerate pairing
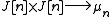
for all n prime to the characteristic of k.
As in the case of elliptic curves, explicit formulae for this pairing can be given in terms of divisors of C.
and algebraic geometry
, and has also been applied in elliptic curve cryptography
and identity based encryption.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weil pairing is a construction of roots of unity by means of functions on an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
E, in such a way as to constitute a pairing
Pairing
The concept of pairing treated here occurs in mathematics.-Definition:Let R be a commutative ring with unity, and let M, N and L be three R-modules.A pairing is any R-bilinear map e:M \times N \to L...
(bilinear form, though with multiplicative notation) on the torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
of E. The name is for André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, who gave an abstract algebraic definition; the corresponding results for elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s were known, and can be expressed simply by use of the Weierstrass sigma function
Weierstrass sigma function
In mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass.-Weierstrass sigma-function:...
.
Formulation
Suppose E is defined over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. Given an integer n > 0 (we require n to be prime to char(K) if char(K)> 0) such that K contains a primitive nth root of unity, then the n-torsion on
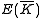has known structure, as a Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of order n. The basis of the construction is of an n-th root of unity
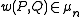
for given points
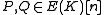, where 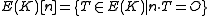and 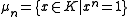, by means of Kummer theoryKummer theory
In abstract algebra and number theory, Kummer theory provides a description of certain types of field extensions involving the adjunction of nth roots of elements of the base field. The theory was originally developed by Ernst Eduard Kummer around the 1840s in his pioneering work on Fermat's last...
.
By a direct argument one can define a function F in the function field
Function field
Function field may refer to:*Function field of an algebraic variety*Function field...
of E over the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K, by its divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
:
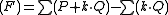
with sums for 0 ≤ k < n. In words F has a simple zero at each point P + kQ, and a simple pole at each point kQ. Then F is well-defined up to multiplication by a constant. If G is the translation of F by Q, then by construction G has the same divisor. One can show that
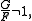
unless P and Q generate cyclic subgroups one of which is inside the other. In fact then G/F would yield a function on the isogenous curve E/C where C is the cyclic subgroup generated by Q, having just one simple pole. Such a function cannot exist, as follows by proving the residue at the pole is zero, a contradiction.
Therefore if we define
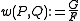
we shall have an n-th root of unity (translating n times must give 1) other than 1. With this definition it can be shown that w is antisymmetric and bilinear, giving rise to a non-degenerate pairing on the n-torsion.
Generalisation to abelian varieties
For abelian varieties over an algebraically closed field K, the Weil pairing is a nondegenerate pairing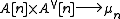for all n prime to the characteristic of k. Here
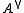denotes the dual abelian varietyDual abelian variety
In mathematics, a dual abelian variety can be defined from an abelian variety A, defined over a field K.-Definition:To an abelian variety A over a field k, one associates a dual abelian variety Av , which is the solution to the following moduli problem...
of A. This is the so-called Weil pairing for higher dimensions. If A is equipped with a polarisation
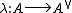,then composition gives a (possibly degenerate) pairing
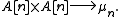
If C is a projective, nonsingular curve of genus ≥ 0 over k, and J its Jacobian
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
, then the theta-divisor
Theta-divisor
In mathematics, the theta divisor Θ is the divisor in the sense of algebraic geometry defined on an abelian variety A over the complex numbers by the zero locus of the associated Riemann theta-function...
of J induces a principal polarisation of J, which in this particular case happens to be an isomorphism (see autoduality of Jacobians). Hence, composing the Weil pairing for J with the polarisation gives a nondegenerate pairing
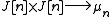
for all n prime to the characteristic of k.
As in the case of elliptic curves, explicit formulae for this pairing can be given in terms of divisors of C.
Applications
The Weil pairing is used in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, and has also been applied in elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
and identity based encryption.
See also
- Pairing-based cryptographyPairing-based cryptographyPairing-based cryptography is the use of a pairing between elements of two cryptographic groups to a third group to construct cryptographic systems. If the same group is used for the first two groups, the pairing is called symmetric and is a mapping from two elements of one group to an element from...
- Boneh/Franklin schemeBoneh/Franklin schemeThe Boneh/Franklin scheme is an Identity based encryption system proposed by Dan Boneh and Matthew K. Franklin in 2001 . This article refers to the protocol version called BasicIdent...
- Homomorphic Signatures for Network CodingHomomorphic signatures for network codingNetwork coding has been shown to optimally use bandwidth in a network, maximizing information flow but the scheme is very inherently vulnerable to pollution attacks by malicious nodes in the network. A node injecting garbage can quickly affect many receivers...