
Homomorphic signatures for network coding
Encyclopedia
Network coding
has been shown to optimally use bandwidth
in a network, maximizing information flow but the scheme is very inherently vulnerable to pollution attacks by malicious nodes in the network. A node injecting garbage can quickly affect many receivers. The pollution of network packets spreads quickly since the output of (even an) honest node is corrupted if at least one of the incoming packets is corrupted. An attacker can easily corrupt a packet even if it is encrypted by either forging the signature or by producing a collision under the hash function
. This will give an attacker access to the packets and the ability to corrupt them. Denis Charles, Kamal Jain and Kristin Lauter designed a new homomorphic encryption
signature scheme for use with network coding to prevent pollution attacks. The homomorphic property of the signatures allows nodes to sign any linear combination of the incoming packets without contacting the signing authority. In this scheme it is computationally infeasible for a node to sign a linear combination of the packets without disclosing what linear combination
was used in the generation of the packet. Furthermore, we can prove that the signature scheme is secure under well known cryptographic
assumptions of the hardness of the discrete logarithm
problem and the computational Elliptic curve Diffie–Hellman.
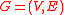 be a directed graph
be a directed graph
where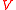 is a set, whose elements are called vertices or node
is a set, whose elements are called vertices or node
s, and is a set of ordered pair
is a set of ordered pair
s of vertices, called arcs, directed edges, or arrows. A source wants to transmit a file
wants to transmit a file  to a set
to a set  of the vertices. One chooses a vector space
of the vertices. One chooses a vector space
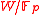 (say of dimension
(say of dimension  ), where
), where 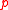 is a prime, and views the data to be transmitted as a bunch of vectors
is a prime, and views the data to be transmitted as a bunch of vectors 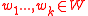 . The source then creates the augmented vectors
. The source then creates the augmented vectors  by setting
by setting  where
where 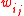 is the
is the 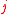 -th coordinate of the vector
-th coordinate of the vector 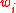 . There are
. There are  zeros before the first '1' appears in
zeros before the first '1' appears in 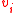 . One can assume without loss of generality that the vectors
. One can assume without loss of generality that the vectors 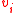 are linearly independent
are linearly independent
. We denote the linear subspace
(of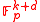 ) spanned by these vectors by
) spanned by these vectors by 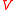 . Each outgoing edge
. Each outgoing edge  computes a linear combination,
computes a linear combination, 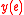 , of the vectors entering the vertex
, of the vectors entering the vertex 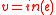 where the edge originates, that is to say
where the edge originates, that is to say
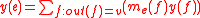
where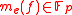 . We consider the source as having
. We consider the source as having  input edges carrying the
input edges carrying the  vectors
vectors 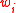 . By induction
. By induction
, one has that the vector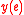 on any edge is a linear combination
on any edge is a linear combination 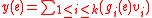 and is a vector in
and is a vector in  . The k-dimensional vector
. The k-dimensional vector 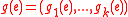 is simply the first k-coordinates of the vector
is simply the first k-coordinates of the vector 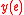 . We call the matrix
. We call the matrix
whose rows are the vectors , where
, where  are the incoming edges for a vertex
are the incoming edges for a vertex 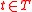 , the global encoding matrix for
, the global encoding matrix for  and denote it as
and denote it as  . In practice the encoding vectors are chosen at random so the matrix
. In practice the encoding vectors are chosen at random so the matrix 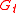 is invertible with high probability. Thus any receiver, on receiving
is invertible with high probability. Thus any receiver, on receiving  can find
can find  by solving
by solving
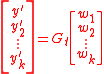
where the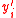 are the vectors formed by removing the first
are the vectors formed by removing the first  coordinates of the vector
coordinates of the vector 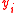 .
.
,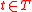 , gets
, gets  vectors
vectors  which are random linear combinations of the
which are random linear combinations of the 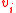 ’s.
’s.
In fact, if
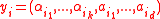
then
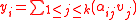 .
.
Thus we can invert the linear transformation to find the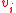 ’s with high probability
’s with high probability
.
 such that:
such that:
Then server can securely distribute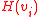 to each receiver, and to check if
to each receiver, and to check if
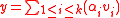
we can check if
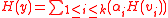
The problem with this method is that the server needs to transfer secure information to each of the receivers. The hash functions needs to be transmitted to all the nodes in the network through a separate secure channel.
needs to be transmitted to all the nodes in the network through a separate secure channel. is expensive to compute and secure transmission of
is expensive to compute and secure transmission of  is not economical either.
is not economical either.
over a finite field is an approach to public-key cryptography
based on the algebraic structure of elliptic curves over finite field
s.
Let be a finite field such that
be a finite field such that 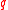 is not a power of 2 or 3. Then an elliptic curve
is not a power of 2 or 3. Then an elliptic curve  over
over 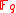 is a curve given by an equation of the form
is a curve given by an equation of the form
 ,
,
where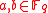 such that
such that 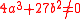
Let , then,
, then,
 forms an abelian group
forms an abelian group
with O as identity. The group operations
can be performed efficiently.
is a construction of roots of unity by means of functions on an elliptic curve
 , in such a way as to constitute a pairing
, in such a way as to constitute a pairing
(bilinear form, though with multiplicative notation) on the torsion subgroup
of . Let
. Let 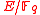 be an elliptic curve and let
be an elliptic curve and let 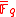 be an algebraic closure of
be an algebraic closure of 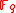 . If
. If  is an integer, relatively prime to the characteristic of the field
is an integer, relatively prime to the characteristic of the field 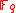 , then the group of
, then the group of  -torsion points,
-torsion points,
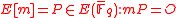 .
.
If is an elliptic curve and
is an elliptic curve and 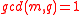 then
then
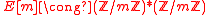
There is a map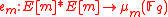 such that:
such that:
Also, can be computed efficiently.
can be computed efficiently.
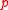 be a prime and
be a prime and 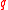 a prime power. Let
a prime power. Let 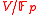 be a vector space of dimension
be a vector space of dimension  and
and 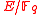 be an elliptic curve such that
be an elliptic curve such that 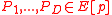 .
.
Define as follows:
as follows:
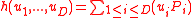 .
.
The function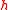 is an arbitrary homomorphism from
is an arbitrary homomorphism from 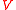 to
to 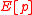 .
.
The server chooses secretly in
secretly in 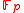 and publishes a point
and publishes a point  of p-torsion such that
of p-torsion such that 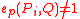 and also publishes
and also publishes 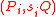 for
for 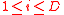 .
.
The signature of the vector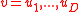 is
is
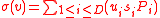
Note: This signature is homomorphic since the computation of h is a homomorphism.
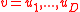 and its signature
and its signature  , verify that
, verify that
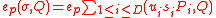
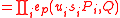
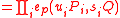
The verification crucially uses the bilinearity of the Weil-pairing.
 for each
for each  . Transmits
. Transmits  .
.
At each edge while computing
while computing
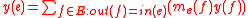
also compute
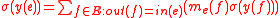
on the elliptic curve .
.
The signature is a point on the elliptic curve with coordinates in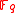 . Thus the size of the signature is
. Thus the size of the signature is 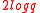 bits (which is some constant times
bits (which is some constant times 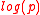 bits, depending on the relative size of
bits, depending on the relative size of 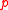 and
and 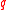 ), and this is the transmission overhead. The computation of the signature
), and this is the transmission overhead. The computation of the signature 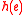 at each vertex requires
at each vertex requires 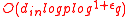 bit operations, where
bit operations, where 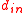 is the in-degree of the vertex
is the in-degree of the vertex 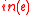 . The verification of a signature requires
. The verification of a signature requires 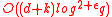 bit operations.
bit operations.
If given points in
points in 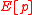 find
find
 and
and 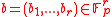
such that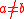 and
and
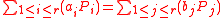 .
.
Proposition: There is a polynomial time reduction from Discrete Log on the cyclic group of order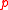 on elliptic curves to Hash-Collision.
on elliptic curves to Hash-Collision.
If , then we get
, then we get  . Thus
. Thus 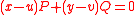 .
.
We claim that and
and 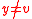 . Suppose that
. Suppose that  , then we would have
, then we would have  , but
, but  is a point of order
is a point of order 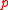 (a prime) thus
(a prime) thus  . In other words
. In other words  in
in 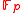 . This contradicts the assumption that
. This contradicts the assumption that 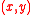 and
and  are distinct pairs in
are distinct pairs in 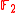 . Thus we have that
. Thus we have that 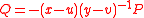 , where the inverse is taken as modulo
, where the inverse is taken as modulo 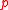 .
.
If we have r > 2 then we can do one of two things. Either we can take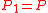 and
and  as before and set
as before and set  for
for  > 2 (in this case the proof reduces to the case when
> 2 (in this case the proof reduces to the case when  ), or we can take
), or we can take  and
and  where
where 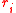 are chosen at random from
are chosen at random from 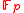 . We get one equation in one unknown (the discrete log of
. We get one equation in one unknown (the discrete log of  ). It is quite possible that the equation we get does not involve the unknown. However, this happens with very small probability as we argue next. Suppose the algorithm for Hash-Collision gave us that
). It is quite possible that the equation we get does not involve the unknown. However, this happens with very small probability as we argue next. Suppose the algorithm for Hash-Collision gave us that
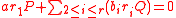 .
.
Then as long as , we can solve for the discrete log of Q. But the
, we can solve for the discrete log of Q. But the 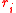 ’s are unknown to the oracle for Hash-Collision and so we can interchange the order in which this process occurs. In other words, given
’s are unknown to the oracle for Hash-Collision and so we can interchange the order in which this process occurs. In other words, given 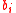 , for
, for 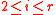 , not all zero, what is the probability that the
, not all zero, what is the probability that the 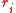 ’s we chose satisfies
’s we chose satisfies 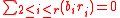 ? It is clear that the latter probability is
? It is clear that the latter probability is  . Thus with high probability we can solve for the discrete log of
. Thus with high probability we can solve for the discrete log of  .
.
We have shown that producing hash collisions in this scheme is difficult. The other method by which an adversary can foil our system is by forging a signature. This scheme for the signature is essentially the Aggregate Signature version of the Boneh-Lynn-Shacham signature scheme. Here it is shown that forging a signature is at least as hard as solving the Elliptic curve Diffie-Hellman
problem. The only known way to solve this problem on elliptic curves is via computing discrete-logs. Thus forging a signature is at least as hard as solving the computational co-Diffie-Hellman on elliptic curves and probably as hard as computing discrete-logs.
Network coding
Network coding is a technique where, instead of simply relaying the packets of information they receive, the nodes of a network will take several packets and combine them together for transmission. This can be used to attain the maximum possible information flow in a network...
has been shown to optimally use bandwidth
Bandwidth (computing)
In computer networking and computer science, bandwidth, network bandwidth, data bandwidth, or digital bandwidth is a measure of available or consumed data communication resources expressed in bits/second or multiples of it .Note that in textbooks on wireless communications, modem data transmission,...
in a network, maximizing information flow but the scheme is very inherently vulnerable to pollution attacks by malicious nodes in the network. A node injecting garbage can quickly affect many receivers. The pollution of network packets spreads quickly since the output of (even an) honest node is corrupted if at least one of the incoming packets is corrupted. An attacker can easily corrupt a packet even if it is encrypted by either forging the signature or by producing a collision under the hash function
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
. This will give an attacker access to the packets and the ability to corrupt them. Denis Charles, Kamal Jain and Kristin Lauter designed a new homomorphic encryption
Homomorphic encryption
Homomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....
signature scheme for use with network coding to prevent pollution attacks. The homomorphic property of the signatures allows nodes to sign any linear combination of the incoming packets without contacting the signing authority. In this scheme it is computationally infeasible for a node to sign a linear combination of the packets without disclosing what linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
was used in the generation of the packet. Furthermore, we can prove that the signature scheme is secure under well known cryptographic
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
assumptions of the hardness of the discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
problem and the computational Elliptic curve Diffie–Hellman.
Network coding
Let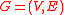 be a directed graph
be a directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
where
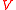 is a set, whose elements are called vertices or node
is a set, whose elements are called vertices or nodeNode (networking)
In communication networks, a node is a connection point, either a redistribution point or a communication endpoint . The definition of a node depends on the network and protocol layer referred to...
s, and
 is a set of ordered pair
is a set of ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of vertices, called arcs, directed edges, or arrows. A source
 wants to transmit a file
wants to transmit a file  to a set
to a set  of the vertices. One chooses a vector space
of the vertices. One chooses a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
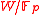 (say of dimension
(say of dimension  ), where
), where 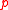 is a prime, and views the data to be transmitted as a bunch of vectors
is a prime, and views the data to be transmitted as a bunch of vectors 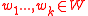 . The source then creates the augmented vectors
. The source then creates the augmented vectors  by setting
by setting  where
where 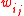 is the
is the 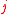 -th coordinate of the vector
-th coordinate of the vector 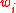 . There are
. There are  zeros before the first '1' appears in
zeros before the first '1' appears in 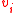 . One can assume without loss of generality that the vectors
. One can assume without loss of generality that the vectors 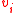 are linearly independent
are linearly independentLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
. We denote the linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
(of
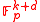 ) spanned by these vectors by
) spanned by these vectors by 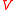 . Each outgoing edge
. Each outgoing edge  computes a linear combination,
computes a linear combination, 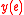 , of the vectors entering the vertex
, of the vectors entering the vertex 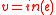 where the edge originates, that is to say
where the edge originates, that is to say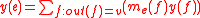
where
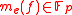 . We consider the source as having
. We consider the source as having  input edges carrying the
input edges carrying the  vectors
vectors 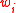 . By induction
. By inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, one has that the vector
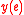 on any edge is a linear combination
on any edge is a linear combination 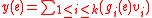 and is a vector in
and is a vector in  . The k-dimensional vector
. The k-dimensional vector 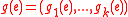 is simply the first k-coordinates of the vector
is simply the first k-coordinates of the vector 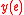 . We call the matrix
. We call the matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose rows are the vectors
 , where
, where  are the incoming edges for a vertex
are the incoming edges for a vertex 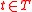 , the global encoding matrix for
, the global encoding matrix for  and denote it as
and denote it as  . In practice the encoding vectors are chosen at random so the matrix
. In practice the encoding vectors are chosen at random so the matrix 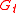 is invertible with high probability. Thus any receiver, on receiving
is invertible with high probability. Thus any receiver, on receiving  can find
can find  by solving
by solving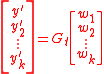
where the
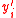 are the vectors formed by removing the first
are the vectors formed by removing the first  coordinates of the vector
coordinates of the vector 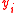 .
.Decoding at the receiver
Each receiverReceiver (Information Theory)
The receiver in information theory is the receiving end of a communication channel. It receives decoded messages/information from the sender, who first encoded them. Sometimes the receiver is modeled so as to include the decoder. Real-world receivers like radio receivers or telephones can not be...
,
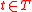 , gets
, gets  vectors
vectors  which are random linear combinations of the
which are random linear combinations of the 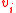 ’s.
’s.In fact, if
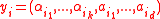
then
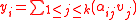 .
.Thus we can invert the linear transformation to find the
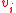 ’s with high probability
’s with high probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
.
History
Krohn, Freedman and Mazieres proposed a theory in 2004 that if we have a hash function such that:
such that:
-
 is collision resistantCollision resistanceCollision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
is collision resistantCollision resistanceCollision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
– it is hard to find and
and  such that
such that 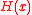 =
= 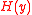 ;
; -
 is a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
is a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
–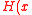 +
+ 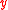 ) =
) =  .
.
Then server can securely distribute
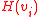 to each receiver, and to check if
to each receiver, and to check if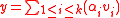
we can check if
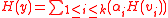
The problem with this method is that the server needs to transfer secure information to each of the receivers. The hash functions
 needs to be transmitted to all the nodes in the network through a separate secure channel.
needs to be transmitted to all the nodes in the network through a separate secure channel. is expensive to compute and secure transmission of
is expensive to compute and secure transmission of  is not economical either.
is not economical either.Advantages of homomorphic signatures
- Establishes authentication in addition to detecting pollution.
- No need for distributing secure hash digests.
- Smaller bit lengths in general will suffice. Signatures of length 180 bits have as much security as 1024 bit RSA signatures.
- Public information does not change for subsequent file transmission.
Signature scheme
The homomorphic property of the signatures allows nodes to sign any linear combination of the incoming packets without contacting the signing authority.Elliptic curves cryptography over a finite field
Elliptic curve cryptographyElliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
over a finite field is an approach to public-key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
based on the algebraic structure of elliptic curves over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Let
 be a finite field such that
be a finite field such that 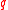 is not a power of 2 or 3. Then an elliptic curve
is not a power of 2 or 3. Then an elliptic curve  over
over 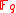 is a curve given by an equation of the form
is a curve given by an equation of the form ,
,where
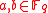 such that
such that 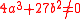
Let
 , then,
, then, forms an abelian group
forms an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
with O as identity. The group operations
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
can be performed efficiently.
Weil pairing
Weil pairingWeil pairing
In mathematics, the Weil pairing is a construction of roots of unity by means of functions on an elliptic curve E, in such a way as to constitute a pairing on the torsion subgroup of E...
is a construction of roots of unity by means of functions on an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
 , in such a way as to constitute a pairing
, in such a way as to constitute a pairingPairing
The concept of pairing treated here occurs in mathematics.-Definition:Let R be a commutative ring with unity, and let M, N and L be three R-modules.A pairing is any R-bilinear map e:M \times N \to L...
(bilinear form, though with multiplicative notation) on the torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
of
 . Let
. Let 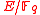 be an elliptic curve and let
be an elliptic curve and let 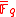 be an algebraic closure of
be an algebraic closure of 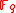 . If
. If  is an integer, relatively prime to the characteristic of the field
is an integer, relatively prime to the characteristic of the field 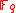 , then the group of
, then the group of  -torsion points,
-torsion points,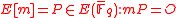 .
.If
 is an elliptic curve and
is an elliptic curve and 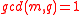 then
then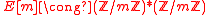
There is a map
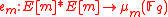 such that:
such that:- (Bilinear)
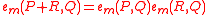 &
& 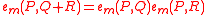 .
. - (Non-degenerate)
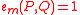 for all P implies that
for all P implies that  .
. - (Alternating)
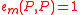 .
.
Also,
 can be computed efficiently.
can be computed efficiently.Homomorphic signatures
Let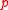 be a prime and
be a prime and 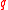 a prime power. Let
a prime power. Let 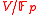 be a vector space of dimension
be a vector space of dimension  and
and 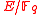 be an elliptic curve such that
be an elliptic curve such that 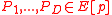 .
.Define
 as follows:
as follows: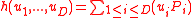 .
.The function
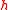 is an arbitrary homomorphism from
is an arbitrary homomorphism from 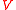 to
to 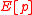 .
.The server chooses
 secretly in
secretly in 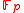 and publishes a point
and publishes a point  of p-torsion such that
of p-torsion such that 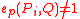 and also publishes
and also publishes 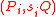 for
for 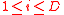 .
.The signature of the vector
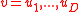 is
is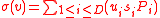
Note: This signature is homomorphic since the computation of h is a homomorphism.
Signature verification
Given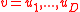 and its signature
and its signature  , verify that
, verify that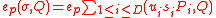
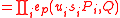
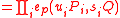
The verification crucially uses the bilinearity of the Weil-pairing.
System setup
The server computes for each
for each  . Transmits
. Transmits  .
.At each edge
 while computing
while computing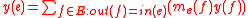
also compute
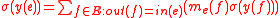
on the elliptic curve
 .
.The signature is a point on the elliptic curve with coordinates in
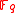 . Thus the size of the signature is
. Thus the size of the signature is 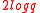 bits (which is some constant times
bits (which is some constant times 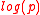 bits, depending on the relative size of
bits, depending on the relative size of 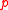 and
and 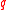 ), and this is the transmission overhead. The computation of the signature
), and this is the transmission overhead. The computation of the signature 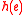 at each vertex requires
at each vertex requires 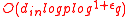 bit operations, where
bit operations, where 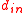 is the in-degree of the vertex
is the in-degree of the vertex 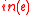 . The verification of a signature requires
. The verification of a signature requires 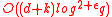 bit operations.
bit operations.Proof of security
Attacker can produce a collision under the hash function.If given
 points in
points in 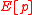 find
find and
and 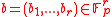
such that
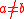 and
and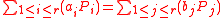 .
.Proposition: There is a polynomial time reduction from Discrete Log on the cyclic group of order
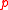 on elliptic curves to Hash-Collision.
on elliptic curves to Hash-Collision.If
 , then we get
, then we get  . Thus
. Thus 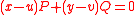 .
.We claim that
 and
and 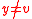 . Suppose that
. Suppose that  , then we would have
, then we would have  , but
, but  is a point of order
is a point of order 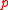 (a prime) thus
(a prime) thus  . In other words
. In other words  in
in 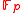 . This contradicts the assumption that
. This contradicts the assumption that 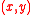 and
and  are distinct pairs in
are distinct pairs in 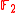 . Thus we have that
. Thus we have that 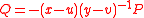 , where the inverse is taken as modulo
, where the inverse is taken as modulo 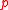 .
.If we have r > 2 then we can do one of two things. Either we can take
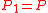 and
and  as before and set
as before and set  for
for  > 2 (in this case the proof reduces to the case when
> 2 (in this case the proof reduces to the case when  ), or we can take
), or we can take  and
and  where
where 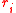 are chosen at random from
are chosen at random from 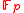 . We get one equation in one unknown (the discrete log of
. We get one equation in one unknown (the discrete log of  ). It is quite possible that the equation we get does not involve the unknown. However, this happens with very small probability as we argue next. Suppose the algorithm for Hash-Collision gave us that
). It is quite possible that the equation we get does not involve the unknown. However, this happens with very small probability as we argue next. Suppose the algorithm for Hash-Collision gave us that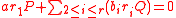 .
.Then as long as
 , we can solve for the discrete log of Q. But the
, we can solve for the discrete log of Q. But the 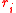 ’s are unknown to the oracle for Hash-Collision and so we can interchange the order in which this process occurs. In other words, given
’s are unknown to the oracle for Hash-Collision and so we can interchange the order in which this process occurs. In other words, given 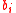 , for
, for 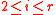 , not all zero, what is the probability that the
, not all zero, what is the probability that the 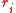 ’s we chose satisfies
’s we chose satisfies 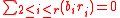 ? It is clear that the latter probability is
? It is clear that the latter probability is  . Thus with high probability we can solve for the discrete log of
. Thus with high probability we can solve for the discrete log of  .
.We have shown that producing hash collisions in this scheme is difficult. The other method by which an adversary can foil our system is by forging a signature. This scheme for the signature is essentially the Aggregate Signature version of the Boneh-Lynn-Shacham signature scheme. Here it is shown that forging a signature is at least as hard as solving the Elliptic curve Diffie-Hellman
Elliptic Curve Diffie-Hellman
Elliptic curve Diffie–Hellman is a key agreement protocol that allows two parties, each having an elliptic curve public-private key pair, to establish a shared secret over an insecure channel. This shared secret may be directly used as a key, or better yet, to derive another key which can then be...
problem. The only known way to solve this problem on elliptic curves is via computing discrete-logs. Thus forging a signature is at least as hard as solving the computational co-Diffie-Hellman on elliptic curves and probably as hard as computing discrete-logs.
See also
- Network codingNetwork codingNetwork coding is a technique where, instead of simply relaying the packets of information they receive, the nodes of a network will take several packets and combine them together for transmission. This can be used to attain the maximum possible information flow in a network...
- Homomorphic EncryptionHomomorphic encryptionHomomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....
- Elliptic Curve CryptographyElliptic curve cryptographyElliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
- Weil pairingWeil pairingIn mathematics, the Weil pairing is a construction of roots of unity by means of functions on an elliptic curve E, in such a way as to constitute a pairing on the torsion subgroup of E...
- Elliptic Curve Diffie-HellmanElliptic Curve Diffie-HellmanElliptic curve Diffie–Hellman is a key agreement protocol that allows two parties, each having an elliptic curve public-private key pair, to establish a shared secret over an insecure channel. This shared secret may be directly used as a key, or better yet, to derive another key which can then be...
- Elliptic Curve DSAElliptic Curve DSAThe Elliptic Curve Digital Signature Algorithm is a variant of the Digital Signature Algorithm which uses Elliptic curve cryptography.-Key and signature size comparison to DSA:...
- Digital Signature AlgorithmDigital Signature AlgorithmThe Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...

