Wolstenholme's theorem
Encyclopedia
In mathematics
, Wolstenholme's theorem states that for a prime number
p > 3, the congruence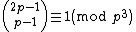
holds, where the parentheses denote a binomial coefficient
. For example, with p = 7, this says that 1716 is one more than a multiple of 343. An equivalent formulation is the congruence
The theorem was first proved by Joseph Wolstenholme
in 1862. In 1819, Charles Babbage
showed the same congruence modulo p2, which holds for all primes p (for p=2 only in the second formulation). The second formulation of Wolstenholme's theorem is due to J. W. L. Glaisher and is inspired by Lucas' theorem.
No known composite number
s satisfy Wolstenholme's theorem and it is conjectured that there are none (see below). A prime that satisfies the congruence modulo p4 is called a Wolstenholme prime
(see below).
As Wolstenholme himself established, his theorem can also be expressed as a pair of congruences for (generalized) harmonic numbers:
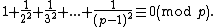
(Congruences with fractions make sense, provided that the denominators are coprime to the modulus.)
For example, with p=7, the first of these says that the numerator of 49/20 is a multiple of 49, while the second says the numerator of 5369/3600 is a multiple of 7.
the following condition holds:
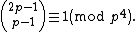
If p is a Wolstenholme prime
, then Glaisher's theorem holds modulo p4. The only known Wolstenholme primes so far are 16843 and 2124679 ; any other Wolstenholme prime must be greater than 109. This result is consistent with the heuristic argument
that the residue modulo
p4 is a pseudo-random multiple of p3. This heuristic predicts that the number of Wolstenholme primes between K and N is roughly ln ln N − ln ln K. The Wolstenholme condition has been checked up to 109, and the heuristic says that there should be roughly one Wolstenholme prime between 109 and 1024. A similar heuristic predicts that there are no "doubly Wolstenholme" primes, meaning that the congruence holds modulo p5.
For the moment let p be any prime, and let a and b be any non-negative integers. Then a set A with ap elements can be divided into a rings of length p, and the rings can be rotated separately. Thus, the group Cpa acts on the set A, and by extension it acts on the set of subsets of size bp. Every orbit of this group action has pk elements, where k is the number of incomplete rings, i.e., if there are k rings that only partly intersect a subset B in the orbit. There are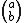
orbits of size 1 and there are no orbits of size p. Thus we first obtain Babbage's theorem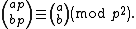
Examining the orbits of size p2, we also obtain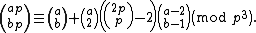
Among other consequences, this equation tells us that the case a=2 and b=1 implies the general case of the second form of Wolstenholme's theorem.
Switching from combinatorics to algebra, both sides of this congruence are polynomials in a for each fixed value of b. The congruence therefore holds when a is any integer, positive or negative, provided that b is a fixed positive integer. In particular, if a=-1 and b=1, the congruence becomes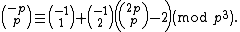
This congruence becomes an equation for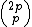
using the relation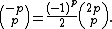
When p is odd, the relation is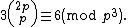
When p≠3, we can divide both sides by 3 to complete the argument.
A similar derivation modulo p4 establishes that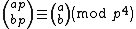
for all positive a and b if and only if it holds when a=2 and b=1, i.e., if and only if p is a Wolstenholme prime.
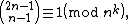
when k=3, then n is prime. The conjecture can be understood by considering k = 1 and 2 as well as 3. When k = 1, Babbage's theorem implies that it holds for n = p2 for p an odd prime, while Wolstenholme's theorem implies that it holds for n = p3 for p > 3. When k = 2, it holds for n = p2 if p is a Wolstenholme prime. Only a few other composite values of n are known when k = 1, and none are known when k = 2, much less k = 3. Thus the conjecture is considered likely because Wolstenholme's congruence seems over-constrained and artificial for composite numbers. Moreover, if the congruence does hold for any particular n other than a prime or prime power, and any particular k, it does not imply that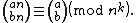
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Wolstenholme's theorem states that for a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p > 3, the congruence
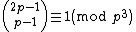
holds, where the parentheses denote a binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. For example, with p = 7, this says that 1716 is one more than a multiple of 343. An equivalent formulation is the congruence
The theorem was first proved by Joseph Wolstenholme
Joseph Wolstenholme
Joseph Wolstenholme was an English mathematician.Wolstenholme was born in Eccles near Salford, Lancashire, England. He graduated from St John's College, Cambridge as Third Wrangler in 1850 and was elected a fellow of Christ's College in 1852...
in 1862. In 1819, Charles Babbage
Charles Babbage
Charles Babbage, FRS was an English mathematician, philosopher, inventor and mechanical engineer who originated the concept of a programmable computer...
showed the same congruence modulo p2, which holds for all primes p (for p=2 only in the second formulation). The second formulation of Wolstenholme's theorem is due to J. W. L. Glaisher and is inspired by Lucas' theorem.
No known composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
s satisfy Wolstenholme's theorem and it is conjectured that there are none (see below). A prime that satisfies the congruence modulo p4 is called a Wolstenholme prime
Wolstenholme prime
In number theory, a Wolstenholme prime is a special type of prime number satisfying a stronger version of Wolstenholme's theorem. Wolstenholme's theorem is a congruence relation satisfied by all prime numbers greater than 7...
(see below).
As Wolstenholme himself established, his theorem can also be expressed as a pair of congruences for (generalized) harmonic numbers:
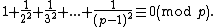
(Congruences with fractions make sense, provided that the denominators are coprime to the modulus.)
For example, with p=7, the first of these says that the numerator of 49/20 is a multiple of 49, while the second says the numerator of 5369/3600 is a multiple of 7.
Wolstenholme primes
A prime p is called a Wolstenholme prime iffIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the following condition holds:
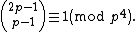
If p is a Wolstenholme prime
Wolstenholme prime
In number theory, a Wolstenholme prime is a special type of prime number satisfying a stronger version of Wolstenholme's theorem. Wolstenholme's theorem is a congruence relation satisfied by all prime numbers greater than 7...
, then Glaisher's theorem holds modulo p4. The only known Wolstenholme primes so far are 16843 and 2124679 ; any other Wolstenholme prime must be greater than 109. This result is consistent with the heuristic argument
Heuristic argument
A heuristic argument is an argument that reasons from the value of a method or principle that has been shown by experimental investigation to be a useful aid in learning, discovery and problem-solving. A widely-used and important example of a heuristic argument is Occam's Razor....
that the residue modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
p4 is a pseudo-random multiple of p3. This heuristic predicts that the number of Wolstenholme primes between K and N is roughly ln ln N − ln ln K. The Wolstenholme condition has been checked up to 109, and the heuristic says that there should be roughly one Wolstenholme prime between 109 and 1024. A similar heuristic predicts that there are no "doubly Wolstenholme" primes, meaning that the congruence holds modulo p5.
A proof of the theorem
There is more than one way to prove Wolstenholme's theorem. Here is a proof that directly establishes Glaisher's version using both combinatorics and algebra.For the moment let p be any prime, and let a and b be any non-negative integers. Then a set A with ap elements can be divided into a rings of length p, and the rings can be rotated separately. Thus, the group Cpa acts on the set A, and by extension it acts on the set of subsets of size bp. Every orbit of this group action has pk elements, where k is the number of incomplete rings, i.e., if there are k rings that only partly intersect a subset B in the orbit. There are
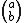orbits of size 1 and there are no orbits of size p. Thus we first obtain Babbage's theorem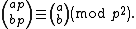Examining the orbits of size p2, we also obtain
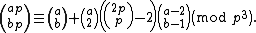
Among other consequences, this equation tells us that the case a=2 and b=1 implies the general case of the second form of Wolstenholme's theorem.
Switching from combinatorics to algebra, both sides of this congruence are polynomials in a for each fixed value of b. The congruence therefore holds when a is any integer, positive or negative, provided that b is a fixed positive integer. In particular, if a=-1 and b=1, the congruence becomes
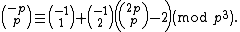
This congruence becomes an equation for
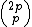using the relation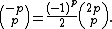When p is odd, the relation is
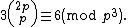
When p≠3, we can divide both sides by 3 to complete the argument.
A similar derivation modulo p4 establishes that
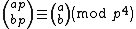
for all positive a and b if and only if it holds when a=2 and b=1, i.e., if and only if p is a Wolstenholme prime.
The converse as a conjecture
It is conjectured that if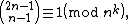when k=3, then n is prime. The conjecture can be understood by considering k = 1 and 2 as well as 3. When k = 1, Babbage's theorem implies that it holds for n = p2 for p an odd prime, while Wolstenholme's theorem implies that it holds for n = p3 for p > 3. When k = 2, it holds for n = p2 if p is a Wolstenholme prime. Only a few other composite values of n are known when k = 1, and none are known when k = 2, much less k = 3. Thus the conjecture is considered likely because Wolstenholme's congruence seems over-constrained and artificial for composite numbers. Moreover, if the congruence does hold for any particular n other than a prime or prime power, and any particular k, it does not imply that
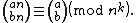
See also
- Fermat's little theoremFermat's little theoremFermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
- Wilson's theorem
- Wieferich primeWieferich primeIn number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1...
- Wilson primeWilson primeA Wilson prime, named after English mathematician John Wilson, is a prime number p such that p2 divides ! + 1, where "!" denotes the factorial function; compare this with Wilson's theorem, which states that every prime p divides ! + 1.The only known Wilson primes are 5, 13, and...
- Wall-Sun-Sun primeWall-Sun-Sun primeIn number theory, a Wall–Sun–Sun prime or Fibonacci–Wieferich prime is a certain kind of prime number which is conjectured to exist although none are known.- Definition :...
- List of special classes of prime numbers