Zero-phonon line and phonon sideband

The zero-phonon line and the phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...

sideband jointly constitute the line

Spectral linewidth

The spectral linewidth characterizes the width of a spectral line, such as in the electromagnetic emission spectrum of an atom, or the frequency spectrum of an acoustic or electronic system...

shape of individual light absorbing and emitting molecules (chromophore

Chromophore

A chromophore is the part of a molecule responsible for its color. The color arises when a molecule absorbs certain wavelengths of visible light and transmits or reflects others. The chromophore is a region in the molecule where the energy difference between two different molecular orbitals falls...

s) embedded into a transparent solid matrix. When the host matrix contains many chromophores, each will contribute a zero-phonon

Phonon

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...

line and a phonon sideband to the absorption and emission spectra

Spectrum

A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...

. The spectra originating from a collection of identical chromophores in a matrix is said to be inhomogeneously broadened because each chromophore is surrounded by a somewhat different matrix environment which modifies the energy required for an electronic transition. In an inhomogeneous distribution of chromophores, individual zero-phonon line and phonon sideband positions are therefore shifted and overlapping.

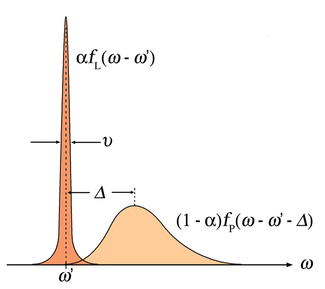
Figure 1 shows the typical line shape for electronic transitions of individual chromophores in a solid matrix. The zero-phonon line is located at a frequency

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

ω’ determined by the intrinsic difference in energy levels between ground and excited state as well as by the local environment. The phonon side band is shifted to a higher frequency in absorption and to a lower frequency in fluorescence. The frequency gap Δ between the zero-phonon line and the peak of the phonon side band is determined by Franck-Condon principle

Franck-Condon principle

The Franck–Condon principle is a rule in spectroscopy and quantum chemistry that explains the intensity of vibronic transitions. Vibronic transitions are the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the...

s.

The distribution of intensity between the zero-phonon line and the phonon side band is strongly dependent on temperature. At room temperature there is enough thermal energy to excite many phonons and the probability of zero-phonon transition is close to zero. For organic chromophores in organic matrices, the probability of a zero-phonon electronic transition only becomes likely below about 40 kelvin

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

s, but depends also on the strength of coupling between the chromophore and the host lattice.

Energy diagram

The transition between the ground

Ground state

The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...

and the excited state

Excited state

Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....

is based on the Franck-Condon principle

Franck-Condon principle

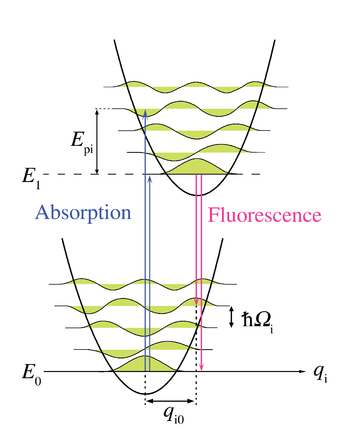
, that the electronic transition is very fast compared with the motion in the lattice. The energy transitions can then be symbolized by vertical arrows between the ground and excited state, that is, there is no motion along the configurational coordinates during the transition. Figure 2 is an energy diagram for interpreting absorption and emission with and without phonons in terms of the configurational coordinate q_i. The energy transitions originate at the lowest phonon energy level of the electronic states. As represented in the figure, the largest wavefunction overlap (and therefore largest transition probability) occurs when the photon

Photon

In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...

energy is equal the energy difference between the two electronic states (E₁ – E₀) plus three quanta

Quantum

In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...

of lattice mode i vibrational energy (

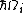). This three phonon transition is mirrored in emission when the excited state quickly decays to its zero-point lattice vibration level by means of a radiationless process, and from there to the ground state via photon emission. The zero-phonon transition is depicted as having a lower wavefunction overlap and therefore a lower transition probability.

In addition to the Franck-Condon assumption, three other approximations are commonly assumed and are implicit in the figures. The first is that each lattice vibrational mode is well described by a quantum harmonic oscillator

Quantum harmonic oscillator

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...

. This approximation is implied in the parabolic

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

shape of the potential wells of Figure 2, and in the equal energy spacing between phonon energy levels. The second approximation is that only the lowest (zero-point) lattice vibration is excited. This is called the low temperature approximation and means that electronic transitions do not originate from any of the higher phonon levels. The third approximation is that the interaction between the chromophore and the lattice is the same in both the ground and the excited state. Specifically, the harmonic oscillator potential is equal in both states. This approximation, called linear coupling, is represented in Figure 2 by two equally shaped parabolic potentials and by equally spaced phonon energy levels in both the ground and excited states.

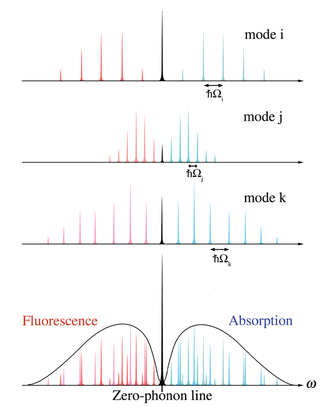
The strength of the zero-phonon transition arises in the superposition of all of the lattice modes. Each lattice mode

Normal mode

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...

m has a characteristic vibrational frequency Ω_m which leads to an energy difference between phonons

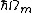. When the transition probabilities for all the modes are summed, the zero-phonon transitions always add at the electronic origin (E₁ – E₀), while the transitions with phonons contribute at a distribution of energies. Figure 3 illustrates the superposition of transition probabilities of several lattice modes. The phonon transition contributions from all lattice modes constitute the phonon sideband.

The frequency separation between the maxima of the absorption and fluorescence phonon sidebands is the phonon contribution to the Stokes’ shift

Stokes shift

Stokes shift is the difference between positions of the band maxima of the absorption and emission spectra of the same electronic transition. It is named after Irish physicist George G. Stokes. When a system absorbs a photon, it gains energy and enters an excited state...

Line shape

The shape of the zero-phonon line is Lorentzian

Lorentzian

Lorentzian may refer to* Cauchy–Lorentz distribution, also known as the Lorentz distribution, Lorentzian function, or Cauchy distribution* Lorentz transformation* Lorentzian inner product* Lorentzian manifoldThe name Lorentz may refer to*Hendrik Lorentz...

with a width determined by the excited state lifetime T₁₀ according to the Heisenberg uncertainty principle

Uncertainty principle

In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...

. Without the influence of the lattice, the natural line width (full width at half maximum) of the chromophore is γ₀ = 1/T₁₀ . The lattice reduces the lifetime of the excited state by introducing radiationless decay mechanisms. At absolute zero

Absolute zero

Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....

the lifetime of the excited state influenced by the lattice is T₁. Above absolute zero, thermal motions will introduce random perturbations to the chromophores local environment. These perturbations shift the energy of the electronic transition, introducing a temperature dependent broadening of the line width. The measured width of a single chromophore’s zero phonon line, the homogeneous line width, is then γ_h(T) ≥ 1/T₁ .

The line shape of the phonon side band is that of a Poisson distribution

Poisson distribution

In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...

as it expresses a discrete number of events, electronic transitions with phonons, during a period of time. At higher temperatures, or when the chromophore interacts strongly with the matrix, the probability of multiphonon is high and the phonon side band approximates a Gaussian distribution.

The distribution of intensity between the zero-phonon line and the phonon sideband is characterized by the Debye-Waller factor

Debye-Waller factor

The Debye–Waller factor , named after Peter Debye and Ivar Waller, is used in condensed matter physics to describe the attenuation of x-ray scattering or coherent neutron scattering caused by thermal motion. It has also been called the B factor or the temperature factor...

α.

Analogy to the Mössbauer effect

The zero-phonon line is an optical analogy to the Mössbauer lines

Mössbauer effect

The Mössbauer effect, or recoilless nuclear resonance fluorescence‎, is a physical phenomenon discovered by Rudolf Mössbauer in 1958. It involves the resonant and recoil-free emission and absorption of γ radiation by atomic nuclei bound in a solid...

, which originate in the recoil-free emission or absorption of gamma ray

Gamma ray

Gamma radiation, also known as gamma rays or hyphenated as gamma-rays and denoted as γ, is electromagnetic radiation of high frequency . Gamma rays are usually naturally produced on Earth by decay of high energy states in atomic nuclei...

s from the nuclei of atoms bound in a solid matrix. In the case of the optical zero-phonon line, the position of the chromophore is the physical parameter that may be perturbed, whereas in the gamma transition, the momenta

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

of the atoms may be changed. More technically, the key to the analogy is the symmetry between position and momentum in the Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

of the quantum harmonic oscillator

Quantum harmonic oscillator

. Both position and momentum contribute in the same way (quadratically) to the total energy.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.