Franck-Condon principle - AbsoluteAstronomy.com

James Franck

James Franck was a German Jewish physicist and Nobel laureate.-Biography:Franck was born to Jacob Franck and Rebecca Nachum Drucker. Franck completed his Ph.D...

–Condon

Edward Condon

Edward Uhler Condon was a distinguished American nuclear physicist, a pioneer in quantum mechanics, and a participant in the development of radar and nuclear weapons during World War II.-Early life and career:...

principle is a rule in spectroscopy

Spectroscopy

Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...

and quantum chemistry

Quantum chemistry

Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...

that explains the intensity of vibronic transition

Vibronic transition

A vibronic transition denotes the simultaneous change of vibrational and electronic quantum number in a molecule. According to the separability of electronic and nuclear motion in the Born-Oppenheimer approximation, the vibrational transition and electronic transition may be described separately...

s. Vibronic transitions are the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon

Photon

In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...

of the appropriate energy. The principle states that during an electronic transition, a change from one vibrational energy level

Energy level

A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...

to another will be more likely to happen if the two vibrational wave functions overlap more significantly.

Overview

The Franck-Condon principle has a well-established semiclassical interpretation based on the original contributions of James Franck

James Franck

James Franck was a German Jewish physicist and Nobel laureate.-Biography:Franck was born to Jacob Franck and Rebecca Nachum Drucker. Franck completed his Ph.D...

[Franck 1926]. Electronic transitions are essentially instantaneous compared with the time scale of nuclear motions, therefore if the molecule is to move to a new vibrational level during the electronic transition, this new vibrational level must be instantaneously compatible with the nuclear

Atomic nucleus

The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...

positions and momenta

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

of the vibrational level of the molecule in the originating electronic state. In the semiclassical picture of vibrations (oscillations) of a simple harmonic oscillator, the necessary conditions can occur at the turning points, where the momentum is zero.

Classically, the Franck–Condon principle is the approximation that an electronic transition is most likely to occur without changes in the positions of the nuclei in the molecular entity and its environment. The resulting state is called a Franck–Condon state, and the transition involved, a vertical transition. The quantum mechanical formulation of this principle is that the intensity of a vibronic transition is proportional to the square of the overlap integral between the vibrational wavefunctions of the two states that are involved in the transition. — IUPAC Compendium of Chemical Terminology, 2nd Edition (1997)

In the quantum mechanical

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

picture, the vibrational levels and vibrational wavefunctions are those of quantum harmonic oscillator

Quantum harmonic oscillator

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...

s, or of more complex approximations to the potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

of molecules, such as the Morse potential

Morse potential

The Morse potential, named after physicist Philip M. Morse, is a convenient model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond...

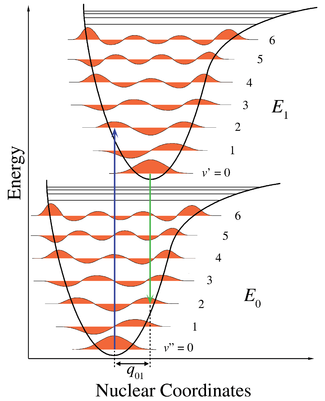
. Figure 1 illustrates the Franck–Condon principle for vibronic transitions in a molecule with Morse-like potential energy functions in both the ground and excited electronic states. In the low temperature approximation, the molecule starts out in the v = 0 vibrational level of the ground electronic state and upon absorbing a photon of the necessary energy, makes a transition to the excited electronic state. The electron configuration of the new state may result in a shift of the equilibrium position of the nuclei constituting the molecule. In the figure this shift in nuclear coordinates between the ground and the first excited state is labeled as q₀₁. In the simplest case of a diatomic

Diatomic

Diatomic molecules are molecules composed only of two atoms, of either the same or different chemical elements. The prefix di- means two in Greek. Common diatomic molecules are hydrogen , nitrogen , oxygen , and carbon monoxide . Seven elements exist in the diatomic state in the liquid and solid...

molecule the nuclear coordinates axis refers to the internuclear separation. The vibronic transition is indicated by a vertical arrow due to the assumption of constant nuclear coordinates during the transition. The probability that the molecule can end up in any particular vibrational level is proportional to the square of the (vertical) overlap of the vibrational wavefunctions of the original and final state (see Quantum mechanical formulation section below). In the electronic excited state molecules quickly relax to the lowest vibrational level (Kasha's rule

Kasha's rule

Kasha's rule is a principle in the photochemistry of electronically excited molecules. The rule states that photon emission occurs in appreciable yield only from the lowest excited state of a given multiplicity...

), and from there can decay to the lowest electronic state via photon emission. The Franck–Condon principle is applied equally to absorption and to fluorescence

Fluorescence

Fluorescence is the emission of light by a substance that has absorbed light or other electromagnetic radiation of a different wavelength. It is a form of luminescence. In most cases, emitted light has a longer wavelength, and therefore lower energy, than the absorbed radiation...

.

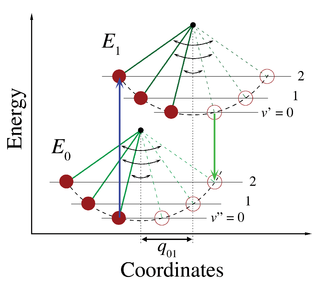
The applicability of the Franck–Condon principle in both absorption and fluorescence, along with Kasha's rule leads to an approximate mirror symmetry shown in Figure 2. The vibrational structure of molecules in a cold, sparse gas is most clearly visible due to the absence of inhomogeneous broadening of the individual transitions. Vibronic transitions are drawn in figure 2 as narrow, equally spaced Lorentzian

Lorentzian

Lorentzian may refer to* Cauchy–Lorentz distribution, also known as the Lorentz distribution, Lorentzian function, or Cauchy distribution* Lorentz transformation* Lorentzian inner product* Lorentzian manifoldThe name Lorentz may refer to*Hendrik Lorentz...

lineshapes. Equal spacing between vibrational levels is only the case for the parabolic

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

potential of simple harmonic oscillators, in more realistic potentials, such as those shown in Figure 1, energy spacing decreases with increasing vibrational energy. Electronic transitions to and from the lowest vibrational states are often referred to as 0-0 (zero zero) transitions and have the same energy in both absorption and fluorescence.

Development of the principle

In a report published in 1926 by the Transactions of the Faraday Society

Faraday Society

The Faraday Society was a British society for the study of physical chemistry, founded in 1903 and named in honour of Michael Faraday. It merged with several similar organisations in 1980 to form the Royal Society of Chemistry...

, James Franck

James Franck

James Franck was a German Jewish physicist and Nobel laureate.-Biography:Franck was born to Jacob Franck and Rebecca Nachum Drucker. Franck completed his Ph.D...

was concerned with the mechanisms of photon-induced chemical reactions. The presumed mechanism was the excitation of a molecule by a photon followed by a collision with another molecule during the short period of excitation. The question was whether it was possible for a molecule to break into photoproducts in a single step, the absorption of a photon, and without a collision. In order for a molecule to break apart it must acquire from the photon vibrational energy exceeding the dissociation energy, that is, the energy to break a chemical bond. However, as was known at the time, molecules will only absorb energy corresponding to allowed quantum transitions and there are no vibrational levels above the dissociation energy level of the potential well

Potential well

A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...

. High energy photon absorption leads to a transition to a higher electronic state instead of dissociation. In examining how much vibrational energy a molecule could acquire when it is excited to a higher electronic level, and whether this vibrational energy could be enough to immediately break apart the molecule, he drew three diagrams representing the possible changes in binding energy between the lowest electronic state and higher electronic states.

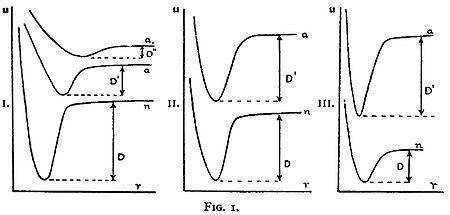
Diagram I. shows a great weakening of the binding on a transition from the normal state n to the excited states a and a. Here we have D > D' and D' > D". At the same time the equilibrium position of the nuclei moves with the excitation to greater values of r. If we go from the equilibrium position (the minimum of potential energy) of the n curve vertically [emphasis added] upwards to the a curves in Diagram I. the particles will have a potential energy greater than D' and will fly apart. In this case we have a very great change in the oscillation energy on excitation by light... — James Franck 1926

James Franck recognized that changes in vibrational levels could be a consequence of the instantaneous nature of excitation to higher electronic energy levels and a new equilibrium position for the nuclear interaction potential. Edward Condon

Edward Condon

extended this insight beyond photoreactions in a 1926 Physical Review

Physical Review

Physical Review is an American scientific journal founded in 1893 by Edward Nichols. It publishes original research and scientific and literature reviews on all aspects of physics. It is published by the American Physical Society. The journal is in its third series, and is split in several...

article titled "A Theory of Intensity Distribution in Band Systems". Here he formulates the semiclassical formulation in a manner quite similar to its modern form. The first joint reference to both Franck and Condon in regards to the new principle appears in the same 1926 issue of Physical Review in an article on the band structure of carbon monoxide

Carbon monoxide

Carbon monoxide , also called carbonous oxide, is a colorless, odorless, and tasteless gas that is slightly lighter than air. It is highly toxic to humans and animals in higher quantities, although it is also produced in normal animal metabolism in low quantities, and is thought to have some normal...

by Raymond Birge

Raymond Thayer Birge

Raymond Thayer Birge was a physicist. Born in Brooklyn, New York, into an academic scientific family, Birge obtained his Doctor's Degree from the University of Wisconsin–Madison in 1913. In the same year he married Irene A. Walsh. The Birges had two children, Carolyn Elizabeth Raymond Thayer...

Quantum mechanical formulation

Consider an electrical dipole

Dipole

In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...

transition from the initial vibrational state (υ) of the ground electronic level (ε),

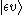, to some vibrational state (υ') of an excited electronic state (ε'),

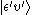(see bra-ket notation

Bra-ket notation

Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...

). The molecular dipole operator μ is determined by the charge (-e) and locations (r_i) of the electrons as well as the charges (+eZ_j) and locations (R_j) of the nuclei

Atomic nucleus

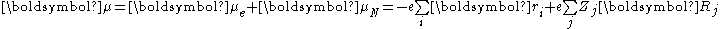
The probability amplitude

Probability amplitude

In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...

P for the transition between these two states is given by

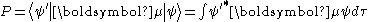
Where

and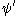

are, respectively, the overall wavefunctions of the initial and final state. The overall wavefunctions are the product of the individual vibrational (depending on spatial coordinates of the nuclei) and electronic space and spin

Spin (physics)

In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...

wavefunctions:

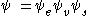
This separation of the electronic and vibrational wavefunctions is an expression of the Born-Oppenheimer approximation

Born-Oppenheimer approximation

In quantum chemistry, the computation of the energy and wavefunction of an average-size molecule is a formidable task that is alleviated by the Born–Oppenheimer approximation, named after Max Born and J. Robert Oppenheimer. For instance the benzene molecule consists of 12 nuclei and 42...

and is the fundamental assumption of the Franck–Condon principle. Combining these equations leads to an expression for the probability amplitude in terms of separate electronic space, spin and vibrational contributions:

The spin-independent part of the initial integral is here approximated as a product of two integrals

This factorization would be exact if the integral

over the spatial coordinates of the electrons would not depend on the nuclear coordinates. However, in the Born-Oppenheimer approximation

and

do depend (parametrically) on the nuclear coordinates, so that the integral (a so-called transition dipole surface) is a function of nuclear coordinates. Since the dependence is usually rather smooth its neglect (i.e., the assumption that the transition dipole surface is independent of nuclear coordinates, called the Condon approximation) is often allowed.

The first integral after the plus sign is equal to zero because electronic wavefunctions of different states are orthogonal. Remaining is the product of three integrals. The first integral is the vibrational overlap integral, also called the Franck-Condon factor. The remaining two integrals contributing to the probability amplitude determine the electronic spatial and spin selection rules.

The Franck–Condon principle is a statement on allowed vibrational transitions between two different electronic states, other quantum mechanical selection rules may lower the probability of a transition or prohibit it altogether. Rotational selection rules have been neglected in the above derivation. Rotational contributions can be observed in the spectra of gases but are strongly suppressed in liquids and solids.

It should be clear that the quantum mechanical formulation of the Franck–Condon principle is the result of a series of approximations, principally the electrical dipole transition assumption and the Born-Oppenheimer approximation. Weaker magnetic dipole and electric quadrupole

Quadrupole

A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...

electronic transitions along with the incomplete validity of the factorization of the total wavefunction into nuclear, electronic spatial and spin wavefunctions means that the selection rules, including the Franck-Condon factor, are not strictly observed. For any given transition, the value of P is determined by all of the selection rules, however spin selection is the largest contributor, followed by electronic selection rules. The Franck-Condon factor only weakly modulates the intensity of transitions, i.e., it contributes with a factor on the order of 1 to the intensity of bands whose order of magnitude is determined by the other selection rules. The table below gives the range of extinction coefficients for the possible combinations of allowed and forbidden spin and orbital selection rules.

Intensities of Electronic Transitions
	Range of extinction coefficient Molar absorptivity The molar absorption coefficient, molar extinction coefficient, or molar absorptivity, is a measurement of how strongly a chemical species absorbs light at a given wavelength... (ε) values (moles Mole (unit) The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value... ⁻¹ cm⁻¹)
Spin and orbitally allowed	10³ to 10⁵
Spin allowed but orbitally forbidden	10⁰ to 10³
Spin forbidden but orbitally allowed	10⁻⁵ to 10⁰

Franck-Condon metaphors in spectroscopy

The Franck–Condon principle, in its canonical form, applies only to changes in the vibrational levels of a molecule in the course of a change in electronic levels by either absorption or emission of a photon. The physical intuition of this principle is anchored by the idea that the nuclear coordinates of the atoms constituting the molecule do not have time to change during the very brief amount of time involved in an electronic transition. However, this physical intuition can be, and is indeed, routinely extended to interactions between light absorbing or emitting molecules (chromophore

Chromophore

A chromophore is the part of a molecule responsible for its color. The color arises when a molecule absorbs certain wavelengths of visible light and transmits or reflects others. The chromophore is a region in the molecule where the energy difference between two different molecular orbitals falls...

s) and their environment. Franck-Condon metaphors are appropriate because molecules often interact strongly with surrounding molecules, particularly in liquids and solids, and these interactions modify the nuclear coordinates of the chromophore in ways which are closely analogous to the molecular vibrations considered by the Franck–Condon principle.

Franck-Condon principle for phonons

The closest Franck-Condon analogy

Analogy

Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...

is due to the interaction of phonons —quanta

Quantum

In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...

of lattice

Crystal structure

In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...

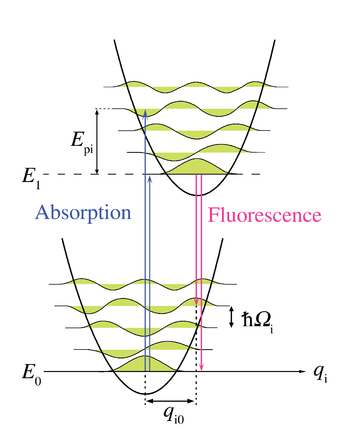
vibrations— with the electronic transitions of chromophores embedded as impurities the lattice. In this situation, transitions to higher electronic levels can take place when the energy of the photon corresponds to the purely electronic transition energy or to the purely electronic transition energy plus the energy of one or more lattice phonons. In the low-temperature approximation, emission is from the zero-phonon

Zero-phonon line and phonon sideband

The zero-phonon line and the phonon sideband jointly constitute the line shape of individual light absorbing and emitting molecules embedded into a transparent solid matrix. When the host matrix contains many chromophores, each will contribute a zero-phonon line and a phonon sideband to the...

level of the excited state to the zero-phonon level of the ground state or to higher phonon levels of the ground state. Just like in the Franck–Condon principle, the probability of transitions involving phonons is determined by the overlap of the phonon wavefunctions at the initial and final energy levels. For the Franck–Condon principle applied to phonon transitions, the label of the horizontal axis of Figure 1 is replaced in Figure 6 with the configurational coordinate for a normal mode

Normal mode

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...

. The lattice mode

potential energy in Figure 6 is represented as that of a harmonic oscillator, and the spacing between phonon levels (

)is determined by lattice parameters. Because the energy of single phonons is generally quite small, zero- or few-phonon transitions can only be observed at temperatures below about 40 kelvins.

See Zero-phonon line and phonon sideband

Zero-phonon line and phonon sideband

for further details and references.

Franck-Condon principle in solvation

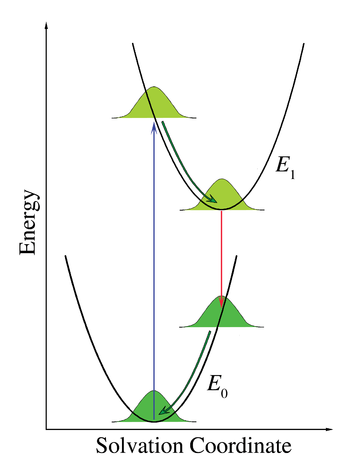
Franck-Condon considerations can also be applied to the electronic transitions of chromophores dissolved in liquids. In this use of the Franck-Condon metaphor, the vibrational levels of the chromophores, as well as interactions of the chromophores with phonons in the liquid, continue to contribute to the structure of the absorption and emission spectra, but these effects are considered separately and independently.

Consider chromophores surrounded by solvent

Solvent

A solvent is a liquid, solid, or gas that dissolves another solid, liquid, or gaseous solute, resulting in a solution that is soluble in a certain volume of solvent at a specified temperature...

molecules. These surrounding molecules may interact with the chromophores, particularly if the solvent molecules are polar

Chemical polarity

In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in...

. This association between solvent and solute

Solution

In chemistry, a solution is a homogeneous mixture composed of only one phase. In such a mixture, a solute is dissolved in another substance, known as a solvent. The solvent does the dissolving.- Types of solutions :...

is referred to as solvation

Solvation

Solvation, also sometimes called dissolution, is the process of attraction and association of molecules of a solvent with molecules or ions of a solute...

and is a stabilizing interaction, that is, the solvent molecules can move and rotate until the energy of the interaction is minimized. The interaction itself involves electrostatic and van der Waals forces and can also include hydrogen bonds. Franck–Condon principles can be applied when the interactions between the chromophore and the surrounding solvent molecules are different in the ground and in the excited electronic state. This change in interaction can originate, for example, due to different dipole moments in these two states. If the chromophore starts in its ground state and is close to equilibrium with the surrounding solvent molecules and then absorbs a photon that takes it to the excited state, its interaction with the solvent will be far from equilibrium in the excited state. This effect is analogous to the original Franck–Condon principle: the electronic transition is very fast compared with the motion of nuclei—the rearrangement of solvent molecules in the case of solvation—. We now speak of a vertical transition, but now the horizontal coordinate is solvent-solute interaction space. This coordinate axis is often labeled as "Solvation Coordinate" and represents, somewhat abstractly, all of the relevant dimensions of motion of all of the interacting solvent molecules.

In the original Franck–Condon principle, after the electronic transition, the molecules which end up in higher vibrational states immediately begin to relax to the lowest vibrational state. In the case of solvation, the solvent molecules will immediately try to rearrange themselves in order to minimize the interaction energy. The rate of solvent relaxation depends on the viscosity

Viscosity

Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...

of the solvent. Assuming the solvent relaxation time is short compared with the lifetime of the electronic excited state, emission will be from the lowest solvent energy state of the excited electronic state. For small-molecule solvents such as water

Water

Water is a chemical substance with the chemical formula H2O. A water molecule contains one oxygen and two hydrogen atoms connected by covalent bonds. Water is a liquid at ambient conditions, but it often co-exists on Earth with its solid state, ice, and gaseous state . Water also exists in a...

or methanol

Methanol

Methanol, also known as methyl alcohol, wood alcohol, wood naphtha or wood spirits, is a chemical with the formula CH3OH . It is the simplest alcohol, and is a light, volatile, colorless, flammable liquid with a distinctive odor very similar to, but slightly sweeter than, ethanol...

at ambient temperature, solvent relaxation time is on the order of some tens of picosecond

Picosecond

A picosecond is 10−12 of a second. That is one trillionth, or one millionth of one millionth of a second, or 0.000 000 000 001 seconds. A picosecond is to one second as one second is to 31,700 years....

s whereas chromophore excited state lifetimes range from a few picoseconds to a few nanoseconds. Immediately after the transition to the ground electronic state, the solvent molecules must also rearrange themselves to accommodate the new electronic configuration of the chromophore. Figure 7 illustrates the Franck–Condon principle applied to solvation. When the solution

Solution

is illuminated by with light corresponding to the electronic transition energy, some of the chromophores will move to the excited state. Within this group of chromophores there will be a statistical distribution of solvent-chromophore interaction energies, represented in the figure by a Gaussian distribution function. The solvent-chromophore interaction is drawn as a parabolic potential in both electronic states. Since the electronic transition is essentially instantaneous on the time scale of solvent motion (vertical arrow), the collection of excited state chromophores is immediately far from equilibrium. The rearrangement of the solvent molecules according to the new potential energy curve is represented by the curved arrows in Figure 7. Note that while the electronic transitions are quantized, the chromophore-solvent interaction energy is treated as a classical continuum due to the large number of molecules involved. Although emission is depicted as taking place from the minimum of the excited state chromophore-solvent interaction potential, significant emission can take place before equilibrium is reached when the viscosity of the solvent is high or the lifetime of the excited state is short. The energy difference between absorbed and emitted photons depicted in Figure 7 is the solvation contribution to the Stokes shift

Stokes shift

Stokes shift is the difference between positions of the band maxima of the absorption and emission spectra of the same electronic transition. It is named after Irish physicist George G. Stokes. When a system absorbs a photon, it gains energy and enters an excited state...

External links

http://www.iupac.org/goldbook/F02510.pdf
http://www.life.uiuc.edu/govindjee/biochem494/Abs.html

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Overview

Development of the principle

Quantum mechanical formulation

Franck-Condon metaphors in spectroscopy

Franck-Condon principle for phonons

Franck-Condon principle in solvation

See also

External links