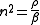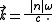Acoustic metamaterials
Encyclopedia
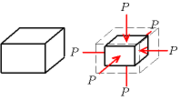
Acoustic metamaterials are artificially fabricated materials designed to control, direct, and manipulate sound
in the form of sonic
, infrasonic, or ultrasonic
waves, as these might occur in gas
es, liquid
s, and solid
s. The hereditary line into acoustic metamaterials follows from theory and research in electromagnetic metamaterials. Furthermore, with acoustic metamaterials, sonic waves can now be extended to the negative refraction
domain.
Control of the various forms of sound wave
s is mostly accomplished through the bulk modulus
β, mass density ρ, and Chirality
. The density and bulk modulus
are analogies of the electromagnetic parameters, permittivity
and permeability
, in electromagnetic metamaterial
s. Related to this is the mechanics of wave propagation in a lattice
structure. Also materials have mass
, and instrinsic degrees of stiffness
. Together, these form a resonant system, and the mechanical (sonic) resonance may be excited by appropriate sonic frequencies (for example pulse
s at audio frequencies).
before that.
Maxwell's equations united all previous observations, experiments and equations of electricity, magnetism and even optics into a consistent theory. Maxwell's equations
demonstrated that electricity, magnetism and even light are all manifestations of the same phenomenon, namely the electromagnetic field
. Subsequently, all other classic laws or equations of these disciplines became simplified cases of Maxwell's equations. Maxwell's achievements concerning electromagnetism have been called the "second great unification in physics", after the first one realised by Isaac Newton
.
Microwave theory had developed significantly just prior to the 20th century with the cylindrical parabolic reflector, dielectric lens, microwave absorbers, the cavity radiator, the radiating iris, and the pyramidal electromagnetic horn. The science involving microwaves also including round square and rectangular waveguides prior to Sir Rayleigh's publilshed results in 1896. Microwave optics, involving the focusing of microwaves, introduced quasi-optical componentes, and a treatment of microwave optics was published in 1897 (by Righi).
In the early part of the twentieth century, Karl Ferdinand Lindman studied wave interaction with collections of metallic helices as artificial chiral media (Annalen der Physik, Vol. 63, No. 4, pp. 621–644, 1920.)
W. E. Kock developed materials that had similar characteristics to metamaterials in the late 1940s Winkler (1956), Tinoco and Freeman (1957), W. Pickering 1970’s, and several other groups in 1980’s and 1990’s in the United States of America.
The modern form of metamaterials was originally proposed by Victor G. Veselago, in 1967. Microwave LH Media domain - Negative refraction (electromagnetic) first demonstrated by D. Smith, S. Shultz, and R. Shelby (2000–2001) Anomalous refraction in DNG Media leads to Pendry's perfect lens proposal (evanescent wave reconstruction). Paired layers of metamaterials with negative permittivity and permeability (DNG) and conventional materials (DPS) follow. In the year 2000 sonic (rubber-silicon coated) crystals in liquid result in the first resonant sonic material (technically not a metamaterial, more of a resonant acoustic material).
The research on acoustic metamaterials began in the year 2000 with the fabrication and demonstration of sonic crystals in a liquid. This was followed by transposing the behavior of the split-ring resonator to research in acoustic metamaterials. After this double negative parameters (negative bulk modulus βeff and negative density ρeff) were produced by this type of medium. Then a group of researchers presented the design and tested results of an ultrasonic metamaterial lens for focusing 60 kHz.
The earlier studies of acoustics in technology, which is called acoustical engineering
, are typically concerned with how to reduce unwanted sounds, noise control
, how to make useful sounds for the medical diagnosis, sonar
, and sound reproduction and how to measure some other physical properties using sound.
Using acoustic metamaterials, the directions of sound through the medium can be controlled, refraction index, so the traditional acoustic technologies extend to controlling the sound wave and even cloak certain matters from acoustic detection.
Similar to metamaterials research, investigating materials with Negative index metamaterials
, the negative index acoustic metamaterials became the primary research. Negative refractive index of acoustic materials can be achieved by changing the bulk modulus
and mass density.
β of a substance reflects the substance's resistance to uniform compression. It is defined in relation to the pressure
increase needed to cause a given relative decrease in volume.
The term mass density
of a material, is interchangeable with density. The latter is defined as mass per unit volume and is expressed in grams per cubic centimeter (g/cm3). In all three classic states of matter — gas, liquid, or solid
— the density varies with a change in temperature or pressure, and gas
es are the most susceptible to those changes. The spectrum of densities is wide ranging: from 1015 g/cm3 for neutron star
s, 1.00 g/cm3 for water to 1.2×10−3 g/cm3 for air. Also relevant here are area density which is mass over a (two-dimensional) area, linear density
- mass over a one-dimensional line, and relative density
, which is a density divided by the density of a reference material, such as water.
For acoustic materials and acoustic metamaterials, both bulk modulus and density are component parameters, which define their refractive index
.
Scientific research revealed that acoustic metamaterials have analogues to electromagnetic metamaterials when exhibiting the following characteristics:
In certain frequency bands, the effective mass density
and bulk modulus
may become negative. This results in a negative refractive index. Flat slab focusing, which can result in super resolution, is similar to electromagnetic metamaterials. The double negative parameters are a result of low-frequency resonance
s. In combination with a well-defined polarization during wave propagation; k = |n|ω, is an equation for refractive index as sound waves interact with acoustic metamaterials (below):
The inherent parameters of the medium are the mass density ρ, bulk modulus β, and chirality k. Chirality, or handedness, determines the polarity of wave propagation
(wave vector
). Hence within the last equation, Veselago-type solutions (n2 = u*ε) are possible for wave propagation as the negative or positive state of ρ and β determine the forward or backward wave propagation.
In negative refractive, electromagnetic metamaterials, negative permittivity can be found in natural materials. However, negative permeability has to be intentionally created in the artificial transmission medium
. Obtaining a negative refractive index with acoustic materials is different.
Neither negative ρ nor negative β are found in naturally occurring materials;
they are derived from the resonant frequencies of an artificially fabricated transmission medium (metamaterial), and such negative values are an anomalous response. Negative ρ or β means that at certain frequencies the medium expands when experiencing compression
(negative modulus), and accelerates to the left when being pushed to the right (negative density).
at the short-wavelength end, covering wavelengths from thousands of kilometers down to a fraction of the size of an atom. That would be wavelengths from 103 to 10−15 kilometers. The long wavelength limit is the size of the universe itself, while it is thought that the short wavelength limit is in the vicinity of the Planck length, although in principle the spectrum is infinite and continuous.
Infrasonic frequencies range from 20 Hz down to 0.001 Hz. Audible frequencies are 20 Hz to 20 kHz. Ultrasonic range is above 20 kHz. Sound requires a medium. Electromagnetics radiation (EM waves) can travel in a vacuum.
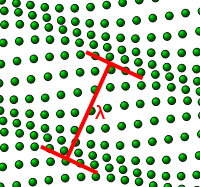An imaginary demonstration: A hypothetical rigid lattice
structure (solid) is composed of 1023 atoms. However, in a real solid these particles could just as easily be ions. In a rigid lattice structure, atoms exert pressure, or a force, on each other in order to maintain equilibrium. Atomic forces maintain rigid lattice structure. Most of them, such as the covalent
or ionic bond
s, are of electric nature. The magnetic force, and the force of gravity are negligible.
Because of bonding between atom
s, the displacement of one or more atoms from their equilibrium positions will give rise to a set of vibration wave
s propagating through the lattice
. One such wave is shown in the figure to the right. The amplitude
of the wave is given by the displacements of the atoms from their equilibrium positions. The wavelength
λ is marked.
There is a minimum possible wavelength, given by the equilibrium separation a between atoms. Any wavelength shorter than this can be mapped onto a wavelength longer than a, due to effects similar to that in aliasing
.
. The key physics
in acoustics
are sound, ultrasound
and infrasound
, which are mechanical waves in gas
es, liquid
s, and solids. One objective of the inquiry into the properties of acoustic metamaterials is applications in seismic wave
reflection and in vibration
control technologies related to earthquake
s.
s. The latter exhibit spectral gaps two orders of magnitude smaller than the wavelength of sound. The spectral gaps prevent the transmission of waves at prescribed frequencies. The frequency can be tuned to desired parameters by varying the size and geometry of the metamaterial.
The fabricated material consisted of a high-density solid lead ball as the core, one centimeter in size, which was coated with a 2.5-mm layer of rubber silicone
. These were arranged in a crystal lattice structure of an 8 × 8 × 8 cube. The balls were cemented into the cubic structure with an epoxy
. Transmission was measured as a function of frequency from 250 to 1600 Hz for effectively a four-layer sonic crystal. A two-centimeter slab absorbed sound that normally would require a much thicker material, at 400 Hz. A drop in amplitude was observed at 400 and 1100 Hz.
The amplitudes of the sound waves entering the surface were compared with the sound waves at the center of the metamaterial structure. The oscillations of the coated spheres absorbed sonic energy, which created the frequency gap; the sound energy is absorbed exponentially as the thickness of the material is increased. The key result here is a negative elastic constant created from resonant frequencies of the material. Its projected applications, with a future expanded frequency range in elastic wave systems, are seismic wave reflection and ultrasonics.
Prior research with SRRs fabricated as negative index electromagnetic metamaterials was referenced as the progenitor of further research in acoustic metamaterials.
An analysis of the frequency band gap characteristics, derived from the inherent limiting properties
of artificially created SRRs, paralleled an analysis of sonic crystals. The band gap properties of SSRs were related to sonic crystal band gap properties. Inherent in this inquiry is a description of mechanical properties and problems
of continuum mechanics
for sonic crystals, as a macroscopically homogeneous substance.
The correlation in bandgap capabilities includes locally resonant elements and elastic moduli which operate in a certain frequency range. Elements which interact and resonate in their respective localized area are embedded throughout the material. In acoustic metamaterials, locally resonant elements would be the interaction of a single 1-cm rubber sphere with the surrounding liquid. The values of the stop band and band gap frequencies can be controlled by choosing the size, types of materials, and the integration of microscopic structures which control the modulation of the frequencies. These materials are then able to shield acoustic
signals and attenuate the effects of anti-plane shear waves. By extrapolating these properties to larger scales it could be possible to create seismic wave filters (see Seismic metamaterials).
According to research
prior to this analysis, arrayed metamaterials can create filters or polarizer
s of either electromagnetic
or elastic waves.
Here a method is shown which can be applied to two-dimensional stop band and bandgap control with either photonic or sonic structures.
Similar to photonic and electromagnetic metamaterial fabrication, a sonic metamaterial is embedded with localized sources of mass density ρ and the (elastic) bulk modulus
β parameters, which are analogous to permittivity and permeability, respectively. The sonic (or phononic) metamaterials are sonic crystals, as in the previous section. These crystals have a solid lead
core and a softer, more elastic silicone
coating. The sonic crystals had built-in localized resonances due to the coated spheres which resulted in almost flat dispersion
curves. Low-frequency bandgaps and localized wave interactions of the coated spheres were analyzed and presented in.
This method can be used to tune bandgaps inherent in the material and, also, create new low-frequency bandgaps. It is also applicable for designing low-frequency phononic crystal waveguides (radio frequency
). Doubly periodic
square array of SRRs are used to illustrate the methodology.
of the material (i.e., elasticity
and mass
). One of the main properties of the phononic crystals is the possibility of having a phononic bandgap. A phononic crystal with phononic bandgap prevents phonons of selected ranges of frequencies from being transmitted through the material
.
To obtain the frequency band structure of a phononic crystal, Bloch theory is applied on a single unit cell in the reciprocal lattice space (Brillouin zone). Several numerical methods are available for this problem, e.g., the planewave expansion method, the finite element method, and the finite difference method. A brief survey of numerical methods for calculating the frequency band structure is provided by Hussein (2009)
In order to speed up the calculation of the frequency band structure, the Reduced Bloch Mode Expansion (RBME) method can be used. The RBME applies "on top" of any of the primary expansion numerical methods mentioned above. For large unit cell models, the RBME method can reduce the time for computing the band structure by up to two orders of magnitude.
The basis of phononic crystals dates back to Isaac Newton
who imagined that sound waves propagated
through air in the same way that an elastic wave would propagate along a lattice
of point masses connected by springs with an elastic force
constant E. This force
constant is identical to the modulus
of the material
. Of course with phononic crystals of materials
with differing modulus the calculations
are a little more complicated than this simple model.
Based on Newton’s observation we can conclude that a key factor for acoustic band-gap engineering
is impedance
mismatch between periodic
elements comprising the crystal and the surrounding medium. When an advancing wave-front
meets a material with very high impedance it will tend to increase its phase velocity
through that medium. Likewise, when the advancing wave-front meets a low impedance medium it will slow down. We can exploit this concept with periodic (and handcrafted) arrangements of impedance mismatched elements to affect acoustic waves in the crystal – essentially band-gap engineering
.
The position of the band-gap in frequency space for a phononic crystal is controlled by the size and arrangement of the elements comprising the crystal. The width of the band gap is generally related to the difference in the speed of sound
(due to impedance differences) through the materials that comprise the composite.
The electromagnetic (isotropic) metamaterials have built-in resonance
structures that exhibit effective negative permittivity and negative permeability for some frequency ranges. In contrast, it is difficult to build composite acoustic materials
with built-in resonances such that the two effective response functions are negative within the capability or range of the transmission medium
.
The mass density ρ and bulk modulus β are position dependent. Using the formulation of a plane wave
the wave vector is:
The angular frequency
is represented by ω and c is the propagation speed of acoustic signal through the homogeneous medium
. With constant density and bulk modulus as constituents of the medium, the refractive index is expressed as n2 = ρ / β. In order to develop a propagating (plane) wave through the material, it is necessary for both ρ and β to be either positive or negative.
When the negative parameters are achieved, the mathematical result of the Poynting vector
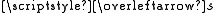. is the opposite direction of the wave vector
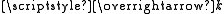. This requires negativity in bulk modulus and density. Physically, it means that the medium displays an anomalous response at some frequencies such that it expands upon compression (negative bulk modulus) and moves to the left when being pushed to the right (negative density) at the same time.
Natural materials do not have a negative density or a negative bulk modulus, but, negative values are mathematically possible, and can be demonstrated when dispersing soft rubber in a liquid.
Even for composite materials, the effective bulk modulus and density should be normally bounded by the values of the constituents, i.e., the derivation of lower and upper bounds for the elastic moduli of the medium. Intrinsic is the expectation for positive bulk modulus and positive density. For example, dispersing spherical solid particles in a fluid results in the ratio governed by the specific gravity when interacting with the long acoustic wavelength (sound). Mathematically, it can be easily proven that βeff and ρeff are definitely positive for natural materials. The exception occurs at low resonant frequencies.
As an example, acoustic double negativity is theoretically demonstrated with a composite of soft, silicone rubber spheres suspended in water. In soft rubber, sound travels much slower than through the water. The high velocity contrast of sound speeds between the rubber spheres and the water allows for the transmission of very low monopolar and dipolar frequencies. This is an analogue to analytical solution for the scattering of electromagnetic radiation, or electromagnetic plane wave scattering
, by spherical particles - dielectric
spheres.
Hence, there is a narrow range of normalized frequency 0.035 < ωa/(2πc) < 0.04 where the bulk modulus and negative density are both negative. Here a is the lattice constant if the spheres are arranged in a face-centered cubic
(fcc) lattice; ω is frequency and c is speed of the acoustic signal. The effective bulk modulus and density near the static limit are positive as predicted. The monopolar resonance creates a negative bulk modulus above the normalized frequency at about 0.035 while the dipolar resonance creates a negative density above the normalized frequency at about 0.04.
This behavior is analogous to low-frequency resonances produced in SRRs (electromagnetic metamaterial). The wires and split rings create intrinsic electric dipolar and magnetic dipolar response. With this artificially constructed acoustic metamaterial of rubber spheres and water, only one structure (instead of two) creates the low-frequency resonances to achieve double negativity. With monopolar resonance, the spheres expand, which produces a phase shift between the waves passing through rubber and water. This creates the negative response. The dipolar resonance creates a negative response such that the frequency of the center of mass of the spheres is out of phase with the wave vector of the sound wave (acoustic signal). If these negative responses are large enough to compensate the background fluid, one can have both negative effective bulk modulus and negative effective density.
Both the mass density and the reciprocal of the bulk modulus are decreasing in magnitude fast enough so that the group velocity becomes negative (double negativity). This gives rise to the desired results of negative refraction. The double negativity is a consequence of resonance
and the resulting negative refraction properties.
structure consisting of one fcc
array of bubble-contained-water spheres (BWSs) and another relatively shifted fcc array of rubber-coated-gold spheres (RGSs) in special epoxy.
Negative bulk modulus is achieved through monopolar resonances of the BWS series. Negative mass density is achieved with dipolar resonances of the gold sphere series. Rather than rubber spheres in liquid, this is a solid based material. This is also as yet a realization of simultaneously negative bulk modulus and mass density in a solid based material, which is an important distinction.
thin ligaments. The DCR cell is a tiny oscillator connected by springs. One spring of the oscillator connects to the mass and is anchored by the other spring. The LC resonator
has specified capacitance and inductance. The limitations are expressed with appropriate mathematical equations. In addition to the intended limitations is that the speed of sound in the matrix is expressed as c = √ρ/µ with a matrix of density ρ and shear modulus μ. The resonant frequency is then expressed as √1/(LC).
A phononic bandgap occurs in association with the resonance of the split cylinder ring. There is a phononic band gap within a range of normalized frequencies. This is when the inclusion moves as a rigid body
.
The DCR design produced a suitable band with negative slope in a range of frequencies. This band was obtained by hybridizing the modes of a DCR with the modes of thin stiff bars. Calculations have shown that at these frequencies:
High-resolution acoustic imaging techniques are the essential tools for nondestructive testing and medical screening. However, the spatial resolution of the conventional acoustic
imaging methods is restricted by the incident wavelength of ultrasound. This is due to the quickly fading evanescent fields
which carry the sub-wavelength features of objects.
The lens consists of a network of fluid-filled cavities called Helmholtz resonators
that oscillate at certain sonic frequencies. Similar to a network of inductors and capacitors in electromagnetic metamaterial, the arrangement of Helmholtz cavities designed by Zhang et al. have a negative dynamic modulus for ultrasound waves. Zhang et al. did focus a point source of 60.5 kHz sound to a spot size that is roughly the width of half a wavelength and their design may allow to push the spatial resolution even further. This result is in excellent agreement with the numerical simulation by transmission line model, which derived the effective mass density and compressibility. This metamaterial lens also displays variable focal length at different frequencies.
allows current to flow in only one direction in a wire; it is an essential electronic device which had no analogues for sound waves. However, the reported design partially fills this role by converting sound to a new frequency and blocking any backwards flow of the original frequency. In practice, it could give designers new flexibility in making ultrasonic sources like those used in medical imaging. The proposed structure combines two components: The first is a sheet of nonlinear acoustic material—one whose sound speed varies with air pressure. An example of such a material is a collection of grains or beads, which becomes stiffer as it is squeezed. The second component is a filter that allows the doubled frequency to pass through but reflects the original.
, China
in a paper in 2007 reported such a metamaterial which simultaneously possessed a negative bulk modulus and mass density.
The metamaterial acoustic cloak is designed to hide objects sumberged in water. The metamaterial cloaking mechanism bends and twists sound waves by intentional design.
The cloaking mechanism consists of 16 concentric rings in a cylindrical configuration, and each ring with acoustic circuits. It is intentionally designed to guide sound waves, in two dimensions. The first microwave metamaterial cloak guided electromagnetic waves in two dimensions.
Each ring has a different index of refraction. This causes sound waves to vary their speed from ring to ring. "The sound waves propagate around the outer ring, guided by the channels in the circuits, which bend the waves to wrap them around the outer layers of the cloak". This device has been described as an array of cavities which actually slow the speed of the propagating sound waves. An experimental cylinder was submerged in tank, and then it disappeared from sonar
. Other objects of various shape and density
were also hidden from the sonar. The acoustic cloak demonstrated effectiveness for the sound wavelengths of 40 kHz to 80 kHz.
Metamaterials scientists
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
in the form of sonic
Supersonic
Supersonic speed is a rate of travel of an object that exceeds the speed of sound . For objects traveling in dry air of a temperature of 20 °C this speed is approximately 343 m/s, 1,125 ft/s, 768 mph or 1,235 km/h. Speeds greater than five times the speed of sound are often...
, infrasonic, or ultrasonic
Ultrasound
Ultrasound is cyclic sound pressure with a frequency greater than the upper limit of human hearing. Ultrasound is thus not separated from "normal" sound based on differences in physical properties, only the fact that humans cannot hear it. Although this limit varies from person to person, it is...
waves, as these might occur in gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es, liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s, and solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
s. The hereditary line into acoustic metamaterials follows from theory and research in electromagnetic metamaterials. Furthermore, with acoustic metamaterials, sonic waves can now be extended to the negative refraction
Negative refraction
Negative refraction is the name for an electromagnetic phenomenon where light rays are refracted at an interface in the reverse sense to that normally expected...
domain.
Control of the various forms of sound wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s is mostly accomplished through the bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
β, mass density ρ, and Chirality
Chirality (electromagnetism)
The term chiral describes an object, especially a molecule, which has or produces a non-superimposeable mirror image of itself. In chemistry, such a molecule is called an enantiomer or is said to exhibit chirality or enantiomerism...
. The density and bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
are analogies of the electromagnetic parameters, permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
and permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
, in electromagnetic metamaterial
Metamaterial
Metamaterials are artificial materials engineered to have properties that may not be found in nature. Metamaterials usually gain their properties from structure rather than composition, using small inhomogeneities to create effective macroscopic behavior....
s. Related to this is the mechanics of wave propagation in a lattice
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
structure. Also materials have mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, and instrinsic degrees of stiffness
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
. Together, these form a resonant system, and the mechanical (sonic) resonance may be excited by appropriate sonic frequencies (for example pulse
Pulse
In medicine, one's pulse represents the tactile arterial palpation of the heartbeat by trained fingertips. The pulse may be palpated in any place that allows an artery to be compressed against a bone, such as at the neck , at the wrist , behind the knee , on the inside of the elbow , and near the...
s at audio frequencies).
History of the acoustic metamaterials
Acoustic metamaterials actually began with electromagnetic metamaterials, and the construction of materials to control electromagnetic radiationElectromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
before that.
Maxwell's equations united all previous observations, experiments and equations of electricity, magnetism and even optics into a consistent theory. Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
demonstrated that electricity, magnetism and even light are all manifestations of the same phenomenon, namely the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. Subsequently, all other classic laws or equations of these disciplines became simplified cases of Maxwell's equations. Maxwell's achievements concerning electromagnetism have been called the "second great unification in physics", after the first one realised by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
.
Microwave theory had developed significantly just prior to the 20th century with the cylindrical parabolic reflector, dielectric lens, microwave absorbers, the cavity radiator, the radiating iris, and the pyramidal electromagnetic horn. The science involving microwaves also including round square and rectangular waveguides prior to Sir Rayleigh's publilshed results in 1896. Microwave optics, involving the focusing of microwaves, introduced quasi-optical componentes, and a treatment of microwave optics was published in 1897 (by Righi).
In the early part of the twentieth century, Karl Ferdinand Lindman studied wave interaction with collections of metallic helices as artificial chiral media (Annalen der Physik, Vol. 63, No. 4, pp. 621–644, 1920.)
W. E. Kock developed materials that had similar characteristics to metamaterials in the late 1940s Winkler (1956), Tinoco and Freeman (1957), W. Pickering 1970’s, and several other groups in 1980’s and 1990’s in the United States of America.
The modern form of metamaterials was originally proposed by Victor G. Veselago, in 1967. Microwave LH Media domain - Negative refraction (electromagnetic) first demonstrated by D. Smith, S. Shultz, and R. Shelby (2000–2001) Anomalous refraction in DNG Media leads to Pendry's perfect lens proposal (evanescent wave reconstruction). Paired layers of metamaterials with negative permittivity and permeability (DNG) and conventional materials (DPS) follow. In the year 2000 sonic (rubber-silicon coated) crystals in liquid result in the first resonant sonic material (technically not a metamaterial, more of a resonant acoustic material).
The research on acoustic metamaterials began in the year 2000 with the fabrication and demonstration of sonic crystals in a liquid. This was followed by transposing the behavior of the split-ring resonator to research in acoustic metamaterials. After this double negative parameters (negative bulk modulus βeff and negative density ρeff) were produced by this type of medium. Then a group of researchers presented the design and tested results of an ultrasonic metamaterial lens for focusing 60 kHz.
The earlier studies of acoustics in technology, which is called acoustical engineering
Acoustical engineering
Acoustical engineering is the branch of engineering dealing with sound and vibration. It is the application of acoustics, the science of sound and vibration, in technology. Acoustical engineers are typically concerned with the manipulation and control of sound....
, are typically concerned with how to reduce unwanted sounds, noise control
Noise control
Noise control is an active or passive means of reducing sound emissions, often incentivised by personal comfort, environmental considerations or legal compliance. Practical and efficient noise control is wholly reliant on an accurate diagnosis of what is causing the noise, which first involves...
, how to make useful sounds for the medical diagnosis, sonar
Sonar
Sonar is a technique that uses sound propagation to navigate, communicate with or detect other vessels...
, and sound reproduction and how to measure some other physical properties using sound.
Using acoustic metamaterials, the directions of sound through the medium can be controlled, refraction index, so the traditional acoustic technologies extend to controlling the sound wave and even cloak certain matters from acoustic detection.
Basic principle
Since the acoustic metamaterials are one of the branch of the metamaterials, the basic principle of the acoustic metamaterials is similar to the principle of metamaterials. These metamaterials usually gain their properties from structure rather than composition, using the inclusion of small inhomogeneities to enact effective macroscopic behavior.Similar to metamaterials research, investigating materials with Negative index metamaterials
Negative index metamaterials
Negative index metamaterials or negative index materials are artificial structures where the refractive index has a negative value over some frequency range. This does not occur in any known natural materials, and thus is only achievable with engineered structures known as metamaterials...
, the negative index acoustic metamaterials became the primary research. Negative refractive index of acoustic materials can be achieved by changing the bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
and mass density.
Bulk modulus and mass density
Below, the bulk modulusBulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
β of a substance reflects the substance's resistance to uniform compression. It is defined in relation to the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
increase needed to cause a given relative decrease in volume.
The term mass density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of a material, is interchangeable with density. The latter is defined as mass per unit volume and is expressed in grams per cubic centimeter (g/cm3). In all three classic states of matter — gas, liquid, or solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
— the density varies with a change in temperature or pressure, and gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es are the most susceptible to those changes. The spectrum of densities is wide ranging: from 1015 g/cm3 for neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s, 1.00 g/cm3 for water to 1.2×10−3 g/cm3 for air. Also relevant here are area density which is mass over a (two-dimensional) area, linear density
Linear density
Linear density, linear mass density or linear mass is a measure of mass per unit of length, and it is a characteristic of strings or other one-dimensional objects. The SI unit of linear density is the kilogram per metre...
- mass over a one-dimensional line, and relative density
Relative density
Relative density, or specific gravity, is the ratio of the density of a substance to the density of a given reference material. Specific gravity usually means relative density with respect to water...
, which is a density divided by the density of a reference material, such as water.
For acoustic materials and acoustic metamaterials, both bulk modulus and density are component parameters, which define their refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
.
Acoustic metamaterial analogues
In certain frequency bands, the effective mass density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
and bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
may become negative. This results in a negative refractive index. Flat slab focusing, which can result in super resolution, is similar to electromagnetic metamaterials. The double negative parameters are a result of low-frequency resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
s. In combination with a well-defined polarization during wave propagation; k = |n|ω, is an equation for refractive index as sound waves interact with acoustic metamaterials (below):
The inherent parameters of the medium are the mass density ρ, bulk modulus β, and chirality k. Chirality, or handedness, determines the polarity of wave propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
(wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
). Hence within the last equation, Veselago-type solutions (n2 = u*ε) are possible for wave propagation as the negative or positive state of ρ and β determine the forward or backward wave propagation.
In negative refractive, electromagnetic metamaterials, negative permittivity can be found in natural materials. However, negative permeability has to be intentionally created in the artificial transmission medium
Transmission medium
A transmission medium is a material substance that can propagate energy waves...
. Obtaining a negative refractive index with acoustic materials is different.
Neither negative ρ nor negative β are found in naturally occurring materials;
they are derived from the resonant frequencies of an artificially fabricated transmission medium (metamaterial), and such negative values are an anomalous response. Negative ρ or β means that at certain frequencies the medium expands when experiencing compression
Gain compression
Gain compression is a reduction in 'differential' or 'slope' gain caused by nonlinearity of the transfer function of the amplifying device. This nonlinearity may be caused by heat due to power dissipation, or by overdriving the active device beyond its linear region...
(negative modulus), and accelerates to the left when being pushed to the right (negative density).
Electromagnetic field vs acoustic field
The electromagnetic spectrum extends from below frequencies used for modern radio to gamma radiationGamma ray
Gamma radiation, also known as gamma rays or hyphenated as gamma-rays and denoted as γ, is electromagnetic radiation of high frequency . Gamma rays are usually naturally produced on Earth by decay of high energy states in atomic nuclei...
at the short-wavelength end, covering wavelengths from thousands of kilometers down to a fraction of the size of an atom. That would be wavelengths from 103 to 10−15 kilometers. The long wavelength limit is the size of the universe itself, while it is thought that the short wavelength limit is in the vicinity of the Planck length, although in principle the spectrum is infinite and continuous.
Infrasonic frequencies range from 20 Hz down to 0.001 Hz. Audible frequencies are 20 Hz to 20 kHz. Ultrasonic range is above 20 kHz. Sound requires a medium. Electromagnetics radiation (EM waves) can travel in a vacuum.
Mechanics of lattice waves
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
structure (solid) is composed of 1023 atoms. However, in a real solid these particles could just as easily be ions. In a rigid lattice structure, atoms exert pressure, or a force, on each other in order to maintain equilibrium. Atomic forces maintain rigid lattice structure. Most of them, such as the covalent
Covalent bond
A covalent bond is a form of chemical bonding that is characterized by the sharing of pairs of electrons between atoms. The stable balance of attractive and repulsive forces between atoms when they share electrons is known as covalent bonding....
or ionic bond
Ionic bond
An ionic bond is a type of chemical bond formed through an electrostatic attraction between two oppositely charged ions. Ionic bonds are formed between a cation, which is usually a metal, and an anion, which is usually a nonmetal. Pure ionic bonding cannot exist: all ionic compounds have some...
s, are of electric nature. The magnetic force, and the force of gravity are negligible.
Because of bonding between atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s, the displacement of one or more atoms from their equilibrium positions will give rise to a set of vibration wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s propagating through the lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. One such wave is shown in the figure to the right. The amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the wave is given by the displacements of the atoms from their equilibrium positions. The wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ is marked.
There is a minimum possible wavelength, given by the equilibrium separation a between atoms. Any wavelength shorter than this can be mapped onto a wavelength longer than a, due to effects similar to that in aliasing
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
.
Acoustic metamaterials analysis and experiments
The current research on acoustic metamaterials is based not only on prior experience with electromagnetic metamaterialsMetamaterial
Metamaterials are artificial materials engineered to have properties that may not be found in nature. Metamaterials usually gain their properties from structure rather than composition, using small inhomogeneities to create effective macroscopic behavior....
. The key physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
in acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
are sound, ultrasound
Ultrasound
Ultrasound is cyclic sound pressure with a frequency greater than the upper limit of human hearing. Ultrasound is thus not separated from "normal" sound based on differences in physical properties, only the fact that humans cannot hear it. Although this limit varies from person to person, it is...
and infrasound
Infrasound
Infrasound is sound that is lower in frequency than 20 Hz or cycles per second, the "normal" limit of human hearing. Hearing becomes gradually less sensitive as frequency decreases, so for humans to perceive infrasound, the sound pressure must be sufficiently high...
, which are mechanical waves in gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es, liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s, and solids. One objective of the inquiry into the properties of acoustic metamaterials is applications in seismic wave
Seismic wave
Seismic waves are waves of energy that travel through the earth, and are a result of an earthquake, explosion, or a volcano that imparts low-frequency acoustic energy. Many other natural and anthropogenic sources create low amplitude waves commonly referred to as ambient vibrations. Seismic waves...
reflection and in vibration
Vibration
Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodic such as the motion of a pendulum or random such as the movement of a tire on a gravel road.Vibration is occasionally "desirable"...
control technologies related to earthquake
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
s.
Sonic crystals
In the year 2000 the research of Liu et al. paved the way to acoustic metamaterials through sonic crystalCrystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s. The latter exhibit spectral gaps two orders of magnitude smaller than the wavelength of sound. The spectral gaps prevent the transmission of waves at prescribed frequencies. The frequency can be tuned to desired parameters by varying the size and geometry of the metamaterial.
The fabricated material consisted of a high-density solid lead ball as the core, one centimeter in size, which was coated with a 2.5-mm layer of rubber silicone
Silicone
Silicones are inert, synthetic compounds with a variety of forms and uses. Typically heat-resistant and rubber-like, they are used in sealants, adhesives, lubricants, medical applications , cookware, and insulation....
. These were arranged in a crystal lattice structure of an 8 × 8 × 8 cube. The balls were cemented into the cubic structure with an epoxy
Epoxy
Epoxy, also known as polyepoxide, is a thermosetting polymer formed from reaction of an epoxide "resin" with polyamine "hardener". Epoxy has a wide range of applications, including fiber-reinforced plastic materials and general purpose adhesives....
. Transmission was measured as a function of frequency from 250 to 1600 Hz for effectively a four-layer sonic crystal. A two-centimeter slab absorbed sound that normally would require a much thicker material, at 400 Hz. A drop in amplitude was observed at 400 and 1100 Hz.
The amplitudes of the sound waves entering the surface were compared with the sound waves at the center of the metamaterial structure. The oscillations of the coated spheres absorbed sonic energy, which created the frequency gap; the sound energy is absorbed exponentially as the thickness of the material is increased. The key result here is a negative elastic constant created from resonant frequencies of the material. Its projected applications, with a future expanded frequency range in elastic wave systems, are seismic wave reflection and ultrasonics.
Split-ring resonators for acoustic metamaterials
In 2004 split-ring resonators (SRR) became the object of acoustic metamaterial research.Prior research with SRRs fabricated as negative index electromagnetic metamaterials was referenced as the progenitor of further research in acoustic metamaterials.
An analysis of the frequency band gap characteristics, derived from the inherent limiting properties
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
of artificially created SRRs, paralleled an analysis of sonic crystals. The band gap properties of SSRs were related to sonic crystal band gap properties. Inherent in this inquiry is a description of mechanical properties and problems
of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
for sonic crystals, as a macroscopically homogeneous substance.
The correlation in bandgap capabilities includes locally resonant elements and elastic moduli which operate in a certain frequency range. Elements which interact and resonate in their respective localized area are embedded throughout the material. In acoustic metamaterials, locally resonant elements would be the interaction of a single 1-cm rubber sphere with the surrounding liquid. The values of the stop band and band gap frequencies can be controlled by choosing the size, types of materials, and the integration of microscopic structures which control the modulation of the frequencies. These materials are then able to shield acoustic
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
signals and attenuate the effects of anti-plane shear waves. By extrapolating these properties to larger scales it could be possible to create seismic wave filters (see Seismic metamaterials).
According to research
Research
Research can be defined as the scientific search for knowledge, or as any systematic investigation, to establish novel facts, solve new or existing problems, prove new ideas, or develop new theories, usually using a scientific method...
prior to this analysis, arrayed metamaterials can create filters or polarizer
Polarizer
A polarizer is an optical filter that passes light of a specific polarization and blocks waves of other polarizations. It can convert a beam of light of undefined or mixed polarization into a beam with well-defined polarization. The common types of polarizers are linear polarizers and circular...
s of either electromagnetic
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
or elastic waves.
Here a method is shown which can be applied to two-dimensional stop band and bandgap control with either photonic or sonic structures.
Similar to photonic and electromagnetic metamaterial fabrication, a sonic metamaterial is embedded with localized sources of mass density ρ and the (elastic) bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
β parameters, which are analogous to permittivity and permeability, respectively. The sonic (or phononic) metamaterials are sonic crystals, as in the previous section. These crystals have a solid lead
Lead
Lead is a main-group element in the carbon group with the symbol Pb and atomic number 82. Lead is a soft, malleable poor metal. It is also counted as one of the heavy metals. Metallic lead has a bluish-white color after being freshly cut, but it soon tarnishes to a dull grayish color when exposed...
core and a softer, more elastic silicone
Silicone
Silicones are inert, synthetic compounds with a variety of forms and uses. Typically heat-resistant and rubber-like, they are used in sealants, adhesives, lubricants, medical applications , cookware, and insulation....
coating. The sonic crystals had built-in localized resonances due to the coated spheres which resulted in almost flat dispersion
Acoustic dispersion
Acoustic dispersion is the phenomenon of a sound wave separating into its component frequencies as it passes through a material. The phase velocity of the sound wave is viewed as a function of frequency...
curves. Low-frequency bandgaps and localized wave interactions of the coated spheres were analyzed and presented in.
This method can be used to tune bandgaps inherent in the material and, also, create new low-frequency bandgaps. It is also applicable for designing low-frequency phononic crystal waveguides (radio frequency
Radio frequency
Radio frequency is a rate of oscillation in the range of about 3 kHz to 300 GHz, which corresponds to the frequency of radio waves, and the alternating currents which carry radio signals...
). Doubly periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
square array of SRRs are used to illustrate the methodology.
Phononic crystal
Phononic crystals are synthetic materials that are formed by periodic variation of the acoustic propertiesAcoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
of the material (i.e., elasticity
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
and mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
). One of the main properties of the phononic crystals is the possibility of having a phononic bandgap. A phononic crystal with phononic bandgap prevents phonons of selected ranges of frequencies from being transmitted through the material
Transmission medium
A transmission medium is a material substance that can propagate energy waves...
.
To obtain the frequency band structure of a phononic crystal, Bloch theory is applied on a single unit cell in the reciprocal lattice space (Brillouin zone). Several numerical methods are available for this problem, e.g., the planewave expansion method, the finite element method, and the finite difference method. A brief survey of numerical methods for calculating the frequency band structure is provided by Hussein (2009)
In order to speed up the calculation of the frequency band structure, the Reduced Bloch Mode Expansion (RBME) method can be used. The RBME applies "on top" of any of the primary expansion numerical methods mentioned above. For large unit cell models, the RBME method can reduce the time for computing the band structure by up to two orders of magnitude.
The basis of phononic crystals dates back to Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
who imagined that sound waves propagated
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
through air in the same way that an elastic wave would propagate along a lattice
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
of point masses connected by springs with an elastic force
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
constant E. This force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
constant is identical to the modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
of the material
Silicon
Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table...
. Of course with phononic crystals of materials
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
with differing modulus the calculations
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
are a little more complicated than this simple model.
Based on Newton’s observation we can conclude that a key factor for acoustic band-gap engineering
Earthquake engineering
Earthquake engineering is the scientific field concerned with protecting society, the natural and the man-made environment from earthquakes by limiting the seismic risk to socio-economically acceptable levels...
is impedance
Acoustic impedance
The acoustic impedance at a particular frequency indicates how much sound pressure is generated by a given air vibration at that frequency. The acoustic impedance Z is frequency dependent and is very useful, for example, for describing the behaviour of musical wind instruments...
mismatch between periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
elements comprising the crystal and the surrounding medium. When an advancing wave-front
Longitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
meets a material with very high impedance it will tend to increase its phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
through that medium. Likewise, when the advancing wave-front meets a low impedance medium it will slow down. We can exploit this concept with periodic (and handcrafted) arrangements of impedance mismatched elements to affect acoustic waves in the crystal – essentially band-gap engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
.
The position of the band-gap in frequency space for a phononic crystal is controlled by the size and arrangement of the elements comprising the crystal. The width of the band gap is generally related to the difference in the speed of sound
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
(due to impedance differences) through the materials that comprise the composite.
Double-negative acoustic metamaterial
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
structures that exhibit effective negative permittivity and negative permeability for some frequency ranges. In contrast, it is difficult to build composite acoustic materials
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
with built-in resonances such that the two effective response functions are negative within the capability or range of the transmission medium
Transmission medium
A transmission medium is a material substance that can propagate energy waves...
.
The mass density ρ and bulk modulus β are position dependent. Using the formulation of a plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
the wave vector is:
The angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
is represented by ω and c is the propagation speed of acoustic signal through the homogeneous medium
Homogeneity (physics)
In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
. With constant density and bulk modulus as constituents of the medium, the refractive index is expressed as n2 = ρ / β. In order to develop a propagating (plane) wave through the material, it is necessary for both ρ and β to be either positive or negative.
When the negative parameters are achieved, the mathematical result of the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
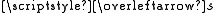. is the opposite direction of the wave vectorWave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
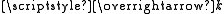. This requires negativity in bulk modulus and density. Physically, it means that the medium displays an anomalous response at some frequencies such that it expands upon compression (negative bulk modulus) and moves to the left when being pushed to the right (negative density) at the same time.Natural materials do not have a negative density or a negative bulk modulus, but, negative values are mathematically possible, and can be demonstrated when dispersing soft rubber in a liquid.
Even for composite materials, the effective bulk modulus and density should be normally bounded by the values of the constituents, i.e., the derivation of lower and upper bounds for the elastic moduli of the medium. Intrinsic is the expectation for positive bulk modulus and positive density. For example, dispersing spherical solid particles in a fluid results in the ratio governed by the specific gravity when interacting with the long acoustic wavelength (sound). Mathematically, it can be easily proven that βeff and ρeff are definitely positive for natural materials. The exception occurs at low resonant frequencies.
As an example, acoustic double negativity is theoretically demonstrated with a composite of soft, silicone rubber spheres suspended in water. In soft rubber, sound travels much slower than through the water. The high velocity contrast of sound speeds between the rubber spheres and the water allows for the transmission of very low monopolar and dipolar frequencies. This is an analogue to analytical solution for the scattering of electromagnetic radiation, or electromagnetic plane wave scattering
Mie theory
The Mie solution to Maxwell's equations describes the scattering of electromagnetic radiation by a sphere...
, by spherical particles - dielectric
Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
spheres.
Hence, there is a narrow range of normalized frequency 0.035 < ωa/(2πc) < 0.04 where the bulk modulus and negative density are both negative. Here a is the lattice constant if the spheres are arranged in a face-centered cubic
Cubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
(fcc) lattice; ω is frequency and c is speed of the acoustic signal. The effective bulk modulus and density near the static limit are positive as predicted. The monopolar resonance creates a negative bulk modulus above the normalized frequency at about 0.035 while the dipolar resonance creates a negative density above the normalized frequency at about 0.04.
This behavior is analogous to low-frequency resonances produced in SRRs (electromagnetic metamaterial). The wires and split rings create intrinsic electric dipolar and magnetic dipolar response. With this artificially constructed acoustic metamaterial of rubber spheres and water, only one structure (instead of two) creates the low-frequency resonances to achieve double negativity. With monopolar resonance, the spheres expand, which produces a phase shift between the waves passing through rubber and water. This creates the negative response. The dipolar resonance creates a negative response such that the frequency of the center of mass of the spheres is out of phase with the wave vector of the sound wave (acoustic signal). If these negative responses are large enough to compensate the background fluid, one can have both negative effective bulk modulus and negative effective density.
Both the mass density and the reciprocal of the bulk modulus are decreasing in magnitude fast enough so that the group velocity becomes negative (double negativity). This gives rise to the desired results of negative refraction. The double negativity is a consequence of resonance
and the resulting negative refraction properties.
Metamaterial with simultaneously negative bulk modulus and mass density
In August 2007 a metamaterial was reported which simultaneously possesses a negative bulk modulus and mass density. This metamaterial is a zinc blendeCubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
structure consisting of one fcc
Cubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
array of bubble-contained-water spheres (BWSs) and another relatively shifted fcc array of rubber-coated-gold spheres (RGSs) in special epoxy.
Negative bulk modulus is achieved through monopolar resonances of the BWS series. Negative mass density is achieved with dipolar resonances of the gold sphere series. Rather than rubber spheres in liquid, this is a solid based material. This is also as yet a realization of simultaneously negative bulk modulus and mass density in a solid based material, which is an important distinction.
Double C resonators
Double C resonator (DCR) is a ring cut in halves. In 2007, proposals have been made for arrays of DCRs and similar negative acoustic metamaterial. Although linear elasticity is mentioned, the problem is defined around shear waves directed at angles to the plane of the cylinders. The DCR was constructed similar to the SRRs in a multiple cell configuration. The DCR has been improved with stiffer material sheets. Each cell consists of a large rigid disk and twothin ligaments. The DCR cell is a tiny oscillator connected by springs. One spring of the oscillator connects to the mass and is anchored by the other spring. The LC resonator
LC circuit
An LC circuit, also called a resonant circuit or tuned circuit, consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C...
has specified capacitance and inductance. The limitations are expressed with appropriate mathematical equations. In addition to the intended limitations is that the speed of sound in the matrix is expressed as c = √ρ/µ with a matrix of density ρ and shear modulus μ. The resonant frequency is then expressed as √1/(LC).
A phononic bandgap occurs in association with the resonance of the split cylinder ring. There is a phononic band gap within a range of normalized frequencies. This is when the inclusion moves as a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
.
The DCR design produced a suitable band with negative slope in a range of frequencies. This band was obtained by hybridizing the modes of a DCR with the modes of thin stiff bars. Calculations have shown that at these frequencies:
- a beam of sound negatively refracts across a slab of such a medium,
- the phase vector in the medium possesses real and imaginary parts with opposite signs,
- the medium is well impedance-matched with the surrounding medium,
- a flat slab of the metamaterial can image a source across the slab like a Veselago lens,
- the image formed by the flat slab has considerable sub-wavelength image resolution, and
- a double corner of the metamaterial can act as an open resonator for sound.
Acoustic metamaterial superlens
In May 2009 Shu Zhang et al. presented the design and test results of an ultrasonic metamaterial lens for focusing 60 kHz (~2 cm wavelength) sound waves under water. The lens is made of sub-wavelength elements and is therefore potentially more compact than phononic lenses that operate in the same frequency range.High-resolution acoustic imaging techniques are the essential tools for nondestructive testing and medical screening. However, the spatial resolution of the conventional acoustic
imaging methods is restricted by the incident wavelength of ultrasound. This is due to the quickly fading evanescent fields
Evanescent wave
An evanescent wave is a nearfield standing wave with an intensity that exhibits exponential decay with distance from the boundary at which the wave was formed. Evanescent waves are a general property of wave-equations, and can in principle occur in any context to which a wave-equation applies...
which carry the sub-wavelength features of objects.
The lens consists of a network of fluid-filled cavities called Helmholtz resonators
Helmholtz resonance
Helmholtz resonance is the phenomenon of air resonance in a cavity, such as when one blows across the top of an empty bottle. The name comes from a device created in the 1850s by Hermann von Helmholtz, the "Helmholtz resonator", which he, the author of the classic study of acoustic science, used to...
that oscillate at certain sonic frequencies. Similar to a network of inductors and capacitors in electromagnetic metamaterial, the arrangement of Helmholtz cavities designed by Zhang et al. have a negative dynamic modulus for ultrasound waves. Zhang et al. did focus a point source of 60.5 kHz sound to a spot size that is roughly the width of half a wavelength and their design may allow to push the spatial resolution even further. This result is in excellent agreement with the numerical simulation by transmission line model, which derived the effective mass density and compressibility. This metamaterial lens also displays variable focal length at different frequencies.
Acoustic diode
An acoustic diode was introduced in August 2009. An electrical diodeDiode
In electronics, a diode is a type of two-terminal electronic component with a nonlinear current–voltage characteristic. A semiconductor diode, the most common type today, is a crystalline piece of semiconductor material connected to two electrical terminals...
allows current to flow in only one direction in a wire; it is an essential electronic device which had no analogues for sound waves. However, the reported design partially fills this role by converting sound to a new frequency and blocking any backwards flow of the original frequency. In practice, it could give designers new flexibility in making ultrasonic sources like those used in medical imaging. The proposed structure combines two components: The first is a sheet of nonlinear acoustic material—one whose sound speed varies with air pressure. An example of such a material is a collection of grains or beads, which becomes stiffer as it is squeezed. The second component is a filter that allows the doubled frequency to pass through but reflects the original.
Acoustic cloaking
An acoustic cloak is a term used to describe technology that would make objects impervious towards sound waves. This can be used to build sound proof homes, advanced concert halls or stealth warships. The mathematics and physics behind acoustic cloaking has been known for several years. The idea of acoustic cloaking is to deviate the sounds waves around the object that has to be cloaked. But realizing it in materials has been difficult. The key to this problem is acoustic metamaterials also known as "Sonic Crystals". Making a metamaterial for sound means identifying the acoustic analogues to permittivity and permeability in light waves. It turns out that these are the material's mass density and its elastic constant. Researchers from Wuhan UniversityWuhan University
Wuhan University is a university located in Wuchang, Hubei, China. It is directly under the administration of the Ministry of Education of the People's Republic of China. It is regarded as one of the top ten universities in China, and its history dates back to 1893, making it one of China's...
, China
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
in a paper in 2007 reported such a metamaterial which simultaneously possessed a negative bulk modulus and mass density.
Potential applications
If such a material could be commercialized, researchers believe it could have many applications. Walls of the material could be built to soundproof houses or it could be used in concert halls to enhance acoustics or direct noise away from certain areas. The military may also be interested to conceal submarines from detection by sonar or to create a new class of stealth ships.Metamaterial acoustic cloak
A laboratory metamaterial device that is applicable to ultra-sound waves has been demonstrated in January 2011. It can be applied to sound wavelengths from 40 to 80 kHz.The metamaterial acoustic cloak is designed to hide objects sumberged in water. The metamaterial cloaking mechanism bends and twists sound waves by intentional design.
The cloaking mechanism consists of 16 concentric rings in a cylindrical configuration, and each ring with acoustic circuits. It is intentionally designed to guide sound waves, in two dimensions. The first microwave metamaterial cloak guided electromagnetic waves in two dimensions.
Each ring has a different index of refraction. This causes sound waves to vary their speed from ring to ring. "The sound waves propagate around the outer ring, guided by the channels in the circuits, which bend the waves to wrap them around the outer layers of the cloak". This device has been described as an array of cavities which actually slow the speed of the propagating sound waves. An experimental cylinder was submerged in tank, and then it disappeared from sonar
Sonar
Sonar is a technique that uses sound propagation to navigate, communicate with or detect other vessels...
. Other objects of various shape and density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
were also hidden from the sonar. The acoustic cloak demonstrated effectiveness for the sound wavelengths of 40 kHz to 80 kHz.
Phononic Metamaterials for Thermal Management
As Phonons are responsible for Thermal conduction in solids, acoustic metamaterials may be designed to control heat transfer.See also
- Acoustic dispersionAcoustic dispersionAcoustic dispersion is the phenomenon of a sound wave separating into its component frequencies as it passes through a material. The phase velocity of the sound wave is viewed as a function of frequency...
- Metamaterial cloakingMetamaterial cloakingMetamaterial cloaking is the scientific application of metamaterials in order to achieve invisibility-cloaking. This is accomplished by manipulating the paths traversed by light through a novel optical material....
- Theories of cloaking
- Chirality (electromagnetism)Chirality (electromagnetism)The term chiral describes an object, especially a molecule, which has or produces a non-superimposeable mirror image of itself. In chemistry, such a molecule is called an enantiomer or is said to exhibit chirality or enantiomerism...
- History of metamaterialsHistory of metamaterialsHistory of metamaterials shares a common history with artificial dielectrics in microwave engineering, as it developed just after World War II. However, there are seminal explorations of artificial materials for manipulating electromagnetic waves at the end of the 19th century...
- MetamaterialMetamaterialMetamaterials are artificial materials engineered to have properties that may not be found in nature. Metamaterials usually gain their properties from structure rather than composition, using small inhomogeneities to create effective macroscopic behavior....
- Metamaterial absorberMetamaterial absorberA metamaterial absorber manipulates the loss components of the complex effective parameters, permittivity and magnetic permeability of metamaterials, to create a material with particularly high absorption...
- Metamaterial antennasMetamaterial antennasMetamaterial antennas are a class of antennas which use metamaterials to increase performance of miniaturized antenna systems. Their purpose, as with any electromagnetic antenna, is to launch energy into free space...
- Negative index metamaterialsNegative index metamaterialsNegative index metamaterials or negative index materials are artificial structures where the refractive index has a negative value over some frequency range. This does not occur in any known natural materials, and thus is only achievable with engineered structures known as metamaterials...
- Nonlinear metamaterialsNonlinear metamaterialsA nonlinear metamaterial is an artificially constructed material that can exhibit properties not found in nature. Its response to electromagnetic radiation can be characterized by its permittivity and material permeability. The product of the permittivity and permeability results in the refractive...
- Photonic metamaterialsPhotonic metamaterialsPhotonic metamaterials, also known as Optical metamaterials, are a type of electromagnetic metamaterial, which are designed to interact with optical frequencies which are terahertz , infrared , and eventually, visible wavelengths. As a type of metamaterial, the periodic structures are made up of...
- Photonic crystalPhotonic crystalPhotonic crystals are periodic optical nanostructures that are designed to affect the motion of photons in a similar way that periodicity of a semiconductor crystal affects the motion of electrons...
- Seismic metamaterialsSeismic metamaterialsSeismic metamaterials, are metamaterials which are designed to counteract the adverse effects of seismic waves on artificial structures, which exist on or near the surface of the earth...
- Split-ring resonator
- SuperlensSuperlensA superlens, super lens or perfect lens is a lens which uses metamaterials to go beyond the diffraction limit. The diffraction limit is an inherent limitation in conventional optical devices or lenses. In 2000, a type of lens was proposed, consisting of a metamaterial that compensates for wave...
- Tunable metamaterialsTunable metamaterialsA tunable metamaterial is a metamaterial with a variable response to an incident electromagnetic wave. This includes remotely controlling how an incident electromagnetic wave interacts with a metamaterial. This means the capablitity to determine whether the EM wave is transmitted, reflected, or...
- Transformation opticsTransformation opticsTransformation optics represents an advancement in the design of optical devices. It is the basis for conceptualizing complex tools in the electromagnetic regime which allows for novel control of light, also known as electromagnetic waves. The mathematics underpinning transformation optics is...
-
-
-
- Books
- Metamaterials HandbookMetamaterials HandbookMetamaterials Handbook is a two-volume handbook on metamaterials edited by Filippo Capolino .The series is designed to cover all theory and application topics related to electromagnetic metamaterials. Disciplines have combined to study, and develop electromagnetic metamaterials...
- Metamaterials: Physics and Engineering ExplorationsMetamaterials: Physics and Engineering ExplorationsMetamaterials: Physics and Engineering Explorations is a book length introduction to the fundamental research and advancements in electromagnetic composite substances known as electromagnetic metamaterials. The discussion encompasses examination of the physics of metamaterial interactions, the...
- Metamaterials Handbook
- Books
-
-
Metamaterials scientists
- Richard W. ZiolkowskiRichard W. ZiolkowskiRichard W. Ziolkowski is a past president of the IEEE Antennas and Propagation Society , and a former vice president of this same society . In 2006 he was awarded OSA Fellow. He is also an IEEE Fellow....
- John PendryJohn PendrySir John Brian Pendry, FRS FInstP is an English theoretical physicist known for his research into refractive indexes and creation of the first practical "Invisibility Cloak"...
- David R. SmithDavid R. SmithDavid R. Smith is a renowned American physicist and professor of electrical and computer engineering at Duke University in North Carolina. Smith's research focuses on electromagnetic metamaterials, or materials with a negative index of refraction...
- Nader EnghetaNader EnghetaNader Engheta is an Iranian scientist and engineer. He has significantly contributed to novel artificial materials, photonics, nano-structured materials, novel graphene materials, and plasmonics....
- Ulf Leonhardt
- Vladimir ShalaevVladimir ShalaevVladimir M. Shalaev , the Robert and Anne Burnett Professor of Electrical and Computer Engineering and Professor of Biomedical Engineering at Purdue University, specializes in metamaterials, transformation optics, nanophotonics and plasmonics...
External links
- Ideas underpinning sound
- Acoustic Metamaterials and Devices: Negative, Positive, and Zero Refraction and Super-lensing in Phononic Crystals
- http://iopscience.iop.org/1367-2630/10/11/115032
- http://news.bbc.co.uk/2/hi/science/nature/7450321.stm
- http://www.newscientist.com/blog/technology/2007/08/how-to-build-acoustic-invisibility.html