Beauville–Laszlo theorem
Encyclopedia
In mathematics
, the Beauville–Laszlo theorem is a result in commutative algebra
and algebraic geometry
that allows one to "glue" two sheaves
over an infinitesimal neighborhood of a point on an algebraic curve
. It was proved by .
result and is stated in its most primitive form for commutative rings. If A is a ring and f is a nonzero element of A, then we can form two derived rings: the localization
at f, Af, and the completion
at Af, Â; both are A-algebra
s. In the following we assume that f is a non-zero divisor. Geometrically, A is viewed as a scheme
X = Spec A and f as a divisor
(f) on Spec A; then Af is its complement Df = Spec Af, the principal open set determined by f, while  is an "infinitesimal neighborhood" D = Spec  of (f). The intersection of Df and Spec  is a "punctured infinitesimal neighborhood" D0 about (f), equal to Spec  ⊗A Af = Spec Âf.
Suppose now that we have an A-module
M; geometrically, M is a sheaf
on Spec A, and we can restrict it to both the principal open set Df and the infinitesimal neighborhood Spec Â, yielding an Af-module F and an Â-module G. Algebraically,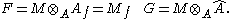
(Despite the notational temptation to write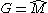
, meaning the completion of the A-module M at the ideal Af, unless A is noetherian
and M is finitely-generated, the two are not in fact equal. This phenomenon is the main reason that the theorem bears the names of Beauville and Laszlo; in the noetherian, finitely-generated case, it is, as noted by the authors, a special case of Grothendieck's faithfully flat descent.) F and G can both be further restricted to the punctured neighborhood D0, and since both restrictions are ultimately derived from M, they are isomorphic: we have an isomorphism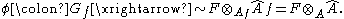
Now consider the converse situation: we have a ring A and an element f, and two modules: an Af-module F and an Â-module G, together with an isomorphism φ as above. Geometrically, we are given a scheme X and both an open set Df and a "small" neighborhood D of its closed complement (f); on Df and D we are given two sheaves which agree on the intersection D0 = Df ∩ D. If D were an open set in the Zariski topology we could glue the sheaves; the content of the Beauville–Laszlo theorem is that, under one technical assumption on f, the same is true for the infinitesimal neighborhood D as well.
Theorem: Given A, f, F, G, and φ as above, if G has no f-torsion, then there exist an A-module M and isomorphisms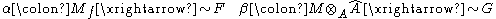
consistent with the isomorphism φ: φ is equal to the composition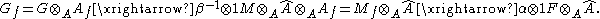
The technical condition that G has no f-torsion is referred to by the authors as "f-regularity". In fact, one can state a stronger version of this theorem. Let M(A) be the category of A-modules (whose morphisms are A-module homomorphisms) and let Mf(A) be the full subcategory of f-regular modules. In this notation, we obtain a commutative diagram
of categories (note Mf(Af) = M(Af)):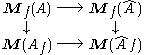
in which the arrows are the base-change maps; for example, the top horizontal arrow acts on objects by M → M ⊗A Â.
Theorem: The above diagram is a cartesian diagram of categories.
on an affine scheme over an infinitesimal neighborhood of a point. Since sheaves have a "local character" and since any scheme is locally affine, the theorem admits a global statement of the same nature. The version of this statement that the authors found noteworthy concerns vector bundles:
Theorem: Let X be an algebraic curve
over a field k, x a k-rational
smooth point
on X with infinitesimal neighborhood D = Spec k
This entails a corollary stated in the paper:
Corollary: With the same setup, denote by Triv(XR) the set of triples (E, τ, σ), where E is a vector bundle on XR, τ is a trivialization of E over (X \ x)R (i.e., an isomorphism with the trivial bundle O(X - x)R), and σ a trivialization over DR. Then the maps in the above diagram furnish a bijection between Triv(XR) and GLr(R((t))) (where R((t)) is the formal Laurent series ring).
The corollary follows from the theorem in that the triple is associated with the unique matrix which, viewed as a "transition function" over D0R between the trivial bundles over (X \ x)R and over DR, allows gluing them to form E, with the natural trivializations of the glued bundle then being identified with σ and τ. The importance of this corollary is that it shows that the affine Grassmannian
may be formed either from the data of bundles over an infinitesimal disk, or bundles on an entire algebraic curve.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Beauville–Laszlo theorem is a result in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
that allows one to "glue" two sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
over an infinitesimal neighborhood of a point on an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
. It was proved by .
The theorem
Although it has implications in algebraic geometry, the theorem is a localLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
result and is stated in its most primitive form for commutative rings. If A is a ring and f is a nonzero element of A, then we can form two derived rings: the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
at f, Af, and the completion
Completion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
at Af, Â; both are A-algebra
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
s. In the following we assume that f is a non-zero divisor. Geometrically, A is viewed as a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
X = Spec A and f as a divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
(f) on Spec A; then Af is its complement Df = Spec Af, the principal open set determined by f, while  is an "infinitesimal neighborhood" D = Spec  of (f). The intersection of Df and Spec  is a "punctured infinitesimal neighborhood" D0 about (f), equal to Spec  ⊗A Af = Spec Âf.
Suppose now that we have an A-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M; geometrically, M is a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on Spec A, and we can restrict it to both the principal open set Df and the infinitesimal neighborhood Spec Â, yielding an Af-module F and an Â-module G. Algebraically,
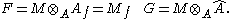
(Despite the notational temptation to write
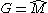, meaning the completion of the A-module M at the ideal Af, unless A is noetherianNoetherian
In mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
and M is finitely-generated, the two are not in fact equal. This phenomenon is the main reason that the theorem bears the names of Beauville and Laszlo; in the noetherian, finitely-generated case, it is, as noted by the authors, a special case of Grothendieck's faithfully flat descent.) F and G can both be further restricted to the punctured neighborhood D0, and since both restrictions are ultimately derived from M, they are isomorphic: we have an isomorphism
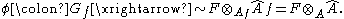
Now consider the converse situation: we have a ring A and an element f, and two modules: an Af-module F and an Â-module G, together with an isomorphism φ as above. Geometrically, we are given a scheme X and both an open set Df and a "small" neighborhood D of its closed complement (f); on Df and D we are given two sheaves which agree on the intersection D0 = Df ∩ D. If D were an open set in the Zariski topology we could glue the sheaves; the content of the Beauville–Laszlo theorem is that, under one technical assumption on f, the same is true for the infinitesimal neighborhood D as well.
Theorem: Given A, f, F, G, and φ as above, if G has no f-torsion, then there exist an A-module M and isomorphisms
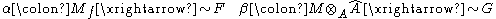
consistent with the isomorphism φ: φ is equal to the composition
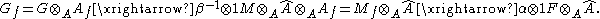
The technical condition that G has no f-torsion is referred to by the authors as "f-regularity". In fact, one can state a stronger version of this theorem. Let M(A) be the category of A-modules (whose morphisms are A-module homomorphisms) and let Mf(A) be the full subcategory of f-regular modules. In this notation, we obtain a commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
of categories (note Mf(Af) = M(Af)):
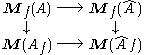
in which the arrows are the base-change maps; for example, the top horizontal arrow acts on objects by M → M ⊗A Â.
Theorem: The above diagram is a cartesian diagram of categories.
Global version
In geometric language, the Beauville–Laszlo theorem allows one to glue sheavesSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on an affine scheme over an infinitesimal neighborhood of a point. Since sheaves have a "local character" and since any scheme is locally affine, the theorem admits a global statement of the same nature. The version of this statement that the authors found noteworthy concerns vector bundles:
Theorem: Let X be an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
over a field k, x a k-rational
Rational point
In number theory, a K-rational point is a point on an algebraic variety where each coordinate of the point belongs to the field K. This means that, if the variety is given by a set of equationsthen the K-rational points are solutions ∈Kn of the equations...
smooth point
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
on X with infinitesimal neighborhood D = Spec k
This entails a corollary stated in the paper:
Corollary: With the same setup, denote by Triv(XR) the set of triples (E, τ, σ), where E is a vector bundle on XR, τ is a trivialization of E over (X \ x)R (i.e., an isomorphism with the trivial bundle O(X - x)R), and σ a trivialization over DR. Then the maps in the above diagram furnish a bijection between Triv(XR) and GLr(R((t))) (where R((t)) is the formal Laurent series ring).
The corollary follows from the theorem in that the triple is associated with the unique matrix which, viewed as a "transition function" over D0R between the trivial bundles over (X \ x)R and over DR, allows gluing them to form E, with the natural trivializations of the glued bundle then being identified with σ and τ. The importance of this corollary is that it shows that the affine Grassmannian
Affine Grassmannian
In mathematics, the term affine Grassmannian has two distinct meanings. In one meaning the affine Grassmannian is the manifold of all k-dimensional affine subspaces of a finite dimensional vector space, while the affine Grassmannian of an algebraic group G over a field k is defined in one of two...
may be formed either from the data of bundles over an infinitesimal disk, or bundles on an entire algebraic curve.