
Beta skeleton
Encyclopedia
In computational geometry
and geometric graph theory
, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
, and calculate an angle θ using the formulas
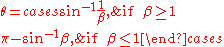
For any two points p and q in the plane, let Rpq be the set of points for which angle prq is greater than θ. Then Rpq takes the form of a union of two open disks with diameter βd(p,q) for β ≥ 1 and θ ≤ π/2, and it takes the form of the intersection of two open disks with diameter d(p,q)/β for β ≤ 1 and θ ≥ π/2. When β = 1 the two formulas give the same value θ = π/2, and Rpq takes the form of a single open disk with pq as its diameter.
The β-skeleton of a discrete set
S of points in the plane is the undirected graph that connects two points p and q with an edge pq whenever Rpq contains no points of S. That is, the β-skeleton is the empty region graph defined by the regions Rpq. When S contains a point r for which angle prq is greater than θ, then pq is not an edge of the β-skeleton; the β-skeleton consists of those pairs pq for which no such point r exists.
(more often called in this context "lunes
"), intersections of two congruent disks with diameter βd(pq), such that line segment pq lies on a radius of both disks and such that the points p and q both lie on the boundary of the intersection. As with the circle-based β-skeleton, the lune-based β-skeleton has an edge pq whenever region Rpq is empty of other input points. For this alternative definition, the relative neighborhood graph
is a special case of a β-skeleton with β = 2. The two definitions coincide for β ≤ 1, and for larger values of β the circle-based skeleton is a subgraph of the lune-based skeleton.
One important difference between the circle-based and lune-based β-skeletons is that, for any point set that does not lie on a single line, there always exists a sufficiently large value of β such that the circle-based β-skeleton is the empty graph. In contrast, if a pair of points p and q has the property that, for all other points r, one of the two angles pqr and qpr is obtuse, then the lune-based β-skeleton will contain edge pq no matter how large β is.
variation of the alpha shape
s of . The name, "β-skeleton", reflects the fact that in some sense the β-skeleton describes the shape of a set of points in the same way that a topological skeleton
describes the shape of a two-dimensional region. Several generalizations of the β-skeleton to graphs defined by other empty regions have also been considered.
to the empty graph. The special case β = 1 leads to the Gabriel graph
, which is known to contain the Euclidean minimum spanning tree
; therefore, the β-skeleton also contains the Gabriel graph and the minimum spanning tree whenever β ≤ 1.
For any constant β, a fractal
construction resembling a flattened version of the Koch snowflake
can be used to define a sequence of point sets whose β-skeletons are paths of arbitrarily large length within a unit square. Therefore, unlike the closely related Delaunay triangulation
, β-skeletons are not geometric spanner
s.
When β ≥ 1, the β-skeleton (with either definition) is a subgraph of the Gabriel graph, which is a subgraph of the Delaunay triangulation
. If pq is an edge of the Delaunay triangulation that is not an edge of the β-skeleton, then a point r that forms a large angle prq can be found as one of the at most two points forming a triangle with p and q in the Delaunay triangulation. Therefore, for these values of β, the circle-based β-skeleton for a set of n points can be constructed in time O(n log n) by computing the Delaunay triangulation and using this test to filter its edges.
For β < 1, a different algorithm of allows the construction of the β-skeleton in time O(n2). No better worst-case time bound is possible because, for any fixed value of β smaller than one, there exist point sets in general position (small perturbations of a regular polygon
) for which the β-skeleton is a complete graph
with a quadratic number of edges. In the same quadratic time bound, the entire β-spectrum (the sequence of circle-based β-skeletons formed by varying β) may also be calculated.
to reconstruct the shape of a two-dimensional object, given a set of sample points on the boundary of the object (a computational form of the connect the dots
puzzle where the sequence in which the dots are to be connected must be deduced by an algorithm rather than being given as part of the puzzle). Although, in general, this requires a choice of the value of the parameter β, it is possible to prove that the choice β = 1.7 will correctly reconstruct the entire boundary of any smooth surface, and not generate any edges that do not belong to the boundary, as long as the samples are generated sufficiently densely relative to the local curvature
of the surface. However in experimental testing a lower value, β = 1.2, was more effective for reconstructing street maps from sets of points marking the center lines of streets in a geographic information system
. For generalizations of the β-skeleton technique to reconstruction of surfaces in three dimensions, see .
Circle-based β-skeletons have been used to find subgraphs of the minimum weight triangulation
of a point set: for sufficiently large values of β, every β-skeleton edge can be guaranteed to belong to the minimum weight triangulation. If the edges found in this way form a connected graph on all of the input points, then the remaining minimum weight triangulation edges may be found in polynomial time by dynamic programming
. However, in general the minimum weight triangulation problem is NP-hard, and the subset of its edges found in this way may not be connected.
β-skeletons have also been applied in machine learning
to solve geometric classification problems and in wireless ad hoc networks as a mechanism for controlling communication complexity by choosing a subset of the pairs of wireless stations that can communicate with each other.
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
and geometric graph theory
Geometric graph theory
In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs...
, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
Circle-based definition
Let β be a positive real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, and calculate an angle θ using the formulas
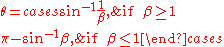
For any two points p and q in the plane, let Rpq be the set of points for which angle prq is greater than θ. Then Rpq takes the form of a union of two open disks with diameter βd(p,q) for β ≥ 1 and θ ≤ π/2, and it takes the form of the intersection of two open disks with diameter d(p,q)/β for β ≤ 1 and θ ≥ π/2. When β = 1 the two formulas give the same value θ = π/2, and Rpq takes the form of a single open disk with pq as its diameter.
The β-skeleton of a discrete set
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
S of points in the plane is the undirected graph that connects two points p and q with an edge pq whenever Rpq contains no points of S. That is, the β-skeleton is the empty region graph defined by the regions Rpq. When S contains a point r for which angle prq is greater than θ, then pq is not an edge of the β-skeleton; the β-skeleton consists of those pairs pq for which no such point r exists.
Lune-based definition
Some authors use an alternative definition in which the empty regions Rpq for β > 1 are not unions of two disks but rather lensesLens (geometry)
In geometry, a lens is a biconvex shape comprising two circular arcs, joined at their endpoints. If the arcs have equal radii, it is called a symmetric lens.A concave-convex shape is called a lune...
(more often called in this context "lunes
Lune (mathematics)
In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.-Plane geometry:...
"), intersections of two congruent disks with diameter βd(pq), such that line segment pq lies on a radius of both disks and such that the points p and q both lie on the boundary of the intersection. As with the circle-based β-skeleton, the lune-based β-skeleton has an edge pq whenever region Rpq is empty of other input points. For this alternative definition, the relative neighborhood graph
Relative neighborhood graph
In computational geometry, the relative neighborhood graph is an undirected graph defined on a set of points in the Euclidean plane by connecting two points p and q by an edge whenever there does not exist a third point r that is closer to both p and q than they are to each other...
is a special case of a β-skeleton with β = 2. The two definitions coincide for β ≤ 1, and for larger values of β the circle-based skeleton is a subgraph of the lune-based skeleton.
One important difference between the circle-based and lune-based β-skeletons is that, for any point set that does not lie on a single line, there always exists a sufficiently large value of β such that the circle-based β-skeleton is the empty graph. In contrast, if a pair of points p and q has the property that, for all other points r, one of the two angles pqr and qpr is obtuse, then the lune-based β-skeleton will contain edge pq no matter how large β is.
History
β-skeletons were first defined by as a scale-invariantScale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
variation of the alpha shape
Alpha shape
In computational geometry, an alpha shape, or α-shape, is a family of piecewise linear simple curves in the Euclidean plane associated with the shape of a finite set of points. They were first defined by . The alpha-shape associated with a set of points is a generalization of the concept of the...
s of . The name, "β-skeleton", reflects the fact that in some sense the β-skeleton describes the shape of a set of points in the same way that a topological skeleton
Topological skeleton
In shape analysis, skeleton of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width...
describes the shape of a two-dimensional region. Several generalizations of the β-skeleton to graphs defined by other empty regions have also been considered.
Properties
If β varies continuously from 0 to ∞, the circle-based β-skeletons form a sequence of graphs extending from the complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
to the empty graph. The special case β = 1 leads to the Gabriel graph
Gabriel graph
In mathematics, the Gabriel graph of a set S of points in the Euclidean plane expresses one notion of proximity or nearness of those points. Formally, it is the graph with vertex set S in which any points P and Q in S are adjacent precisely if they are distinct and the closed disc of which line...
, which is known to contain the Euclidean minimum spanning tree
Euclidean minimum spanning tree
The Euclidean minimum spanning tree or EMST is a minimum spanning tree of a set of n points in the plane , where the weight of the edge between each pair of points is the distance between those two points...
; therefore, the β-skeleton also contains the Gabriel graph and the minimum spanning tree whenever β ≤ 1.
For any constant β, a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
construction resembling a flattened version of the Koch snowflake
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
can be used to define a sequence of point sets whose β-skeletons are paths of arbitrarily large length within a unit square. Therefore, unlike the closely related Delaunay triangulation
Delaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
, β-skeletons are not geometric spanner
Geometric spanner
A geometric spanner or a k-spanner graph or a k-spanner was initially introduced as a weighted graph over a set of points as its vertices which for every pair of vertices has a path between them of weight at most k times the spatial distance between these points for a fixed k...
s.
Algorithms
A naïve algorithm that tests each triple p, q, and r for membership of r in the region Rpq can construct the β-skeleton of any set of n points in time O(n3).When β ≥ 1, the β-skeleton (with either definition) is a subgraph of the Gabriel graph, which is a subgraph of the Delaunay triangulation
Delaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
. If pq is an edge of the Delaunay triangulation that is not an edge of the β-skeleton, then a point r that forms a large angle prq can be found as one of the at most two points forming a triangle with p and q in the Delaunay triangulation. Therefore, for these values of β, the circle-based β-skeleton for a set of n points can be constructed in time O(n log n) by computing the Delaunay triangulation and using this test to filter its edges.
For β < 1, a different algorithm of allows the construction of the β-skeleton in time O(n2). No better worst-case time bound is possible because, for any fixed value of β smaller than one, there exist point sets in general position (small perturbations of a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
) for which the β-skeleton is a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
with a quadratic number of edges. In the same quadratic time bound, the entire β-spectrum (the sequence of circle-based β-skeletons formed by varying β) may also be calculated.
Applications
The circle-based β-skeleton may be used in image analysisImage analysis
Image analysis is the extraction of meaningful information from images; mainly from digital images by means of digital image processing techniques...
to reconstruct the shape of a two-dimensional object, given a set of sample points on the boundary of the object (a computational form of the connect the dots
Connect the dots
Connect the dots, also known as dot to dot or join the dots is a form of puzzle containing a sequence of numbered dots. When a line is drawn connecting the dots the outline of an object is revealed. The puzzles often contain simple line art to enhance the image created or to assist in rendering a...
puzzle where the sequence in which the dots are to be connected must be deduced by an algorithm rather than being given as part of the puzzle). Although, in general, this requires a choice of the value of the parameter β, it is possible to prove that the choice β = 1.7 will correctly reconstruct the entire boundary of any smooth surface, and not generate any edges that do not belong to the boundary, as long as the samples are generated sufficiently densely relative to the local curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the surface. However in experimental testing a lower value, β = 1.2, was more effective for reconstructing street maps from sets of points marking the center lines of streets in a geographic information system
Geographic Information System
A geographic information system, geographical information science, or geospatial information studies is a system designed to capture, store, manipulate, analyze, manage, and present all types of geographically referenced data...
. For generalizations of the β-skeleton technique to reconstruction of surfaces in three dimensions, see .
Circle-based β-skeletons have been used to find subgraphs of the minimum weight triangulation
Minimum weight triangulation
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal weight...
of a point set: for sufficiently large values of β, every β-skeleton edge can be guaranteed to belong to the minimum weight triangulation. If the edges found in this way form a connected graph on all of the input points, then the remaining minimum weight triangulation edges may be found in polynomial time by dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
. However, in general the minimum weight triangulation problem is NP-hard, and the subset of its edges found in this way may not be connected.
β-skeletons have also been applied in machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
to solve geometric classification problems and in wireless ad hoc networks as a mechanism for controlling communication complexity by choosing a subset of the pairs of wireless stations that can communicate with each other.

