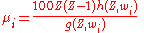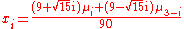Bring radical
Encyclopedia
In algebra
, a Bring radical or ultraradical of a complex number
a is a root of the polynomial
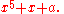
(The root is chosen so the radical of a real number
is real, and the radical is a differentiable function of a in the complex plane, with a branch cut along the negative real line below −1. See the "Bring radicals" section below.)
George Jerrard
(1804–1863) showed that some quintic equation
s can be solved using radicals
and Bring radicals, which had been introduced by Erland Bring
(1736–1798). They can be used to obtain closed-form solutions of quintic equations.
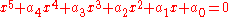
The various methods for solving the quintic that have been developed generally attempt to simplify the quintic using Tschirnhaus transformation
s to reduce the number of independent coefficients.
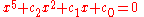
If the roots of a general quintic and a principal quintic are related by a quadratic Tschirnhaus transformation:
the coefficients α and β may be determined by using the resultant, or by means of the power-sum formulae of the quintic roots. This leads to a system of equations in α and β consisting of a quadratic and a linear equation, and either of the two sets of solutions may be used to obtain the corresponding three coefficients of the principal quintic form.
This form is used by Felix Klein
's solution to the quintic.
Using the power-sum formulae again with a cubic transformation as Tschirnhaus
tried does not work, since the resulting system of equations results in a sixth-degree equation.
In 1796 Bring
found a way around this by using a quartic Tschirnhaus transformation to relate the roots of a principal quintic to those of a Bring–Jerrard quintic:
The extra parameter this fourth-order transformation provides allowed Bring to decrease the degrees of the other parameters. This leads to a system of five equations in six unknowns, which then requires the solution of a cubic and a quadratic equation. This method was also discovered by Jerrard
in 1852, but it is likely that he was unaware of Bring's previous work in this area. The full transformation may readily be accomplished using a computer algebra package such as Mathematica
or Maple
. As might be expected from the complexity of these transformations, the resulting expressions can be enormous, particularly when compared to the solutions in radicals for lower degree equations, taking many megabytes of storage for a general quintic with symbolic coefficients.
Regarded as an algebraic function, the solutions to
involve two variables, d1 and d0, however the reduction is actually to an algebraic function of one variable, very much analogous to a solution in radicals, since we may further reduce the Bring–Jerrard form. If we for instance set
then we reduce the equation to the form
which involves z as an algebraic function of a single variable t, where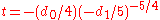
. A similar transformation suffices to reduce the equation to
which is the form required by the Hermite-Kronecker-Brioschi method, Glasser's method, and the Cockle-Harley method of differential resolvents described below.
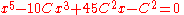
which can be derived by using the following rational Tschirnhaus transformation
to relate the roots of a principal quintic to a Brioschi quintic. The values of the parameters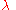
and 
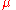may be derived by using polyhedral functions on the Riemann sphere
, and is related to the partition of an object of icosahedral symmetry
into five objects of tetrahedral symmetry
.
It is to be noted that this Tschirnhaus transformation is rather simpler than the difficult one used to transform a principal quintic into Bring–Jerrard form. This normal form is used by the Doyle–McMullen iteration method and the Kiepert method.
for Bring radicals, as well as a representation in terms of hypergeometric functions can be derived as follows. The equation
can be rewritten as 
; by setting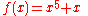 
, the desired solution is 
.
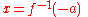The series for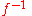
can then be obtained by reversion
of the Taylor series
for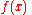
(which is simply 
), giving:
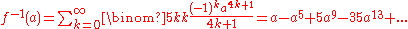
where the absolute values of the coefficients are sequence A002294 in the OEIS
. The series confirms that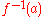
is odd. This gives
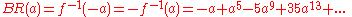
The series converges for |z| < 1 and can be analytically continued in the complex plane. The above result can be written in hypergeometric form as:
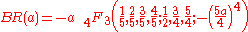
Compare with the hypergeometric functions that arise in Glasser's derivation and the method of differential resolvents below.
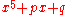
in terms of the Bring radical as
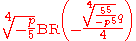
and its four conjugate
s. We have a reduction to the Bring–Jerrard form in terms of solvable polynomial equations, and we used transformations involving polynomial expressions in the roots only up to the fourth degree, which means inverting the transformation may be done by finding the roots of a polynomial solvable in radicals. This procedure produces extraneous solutions, but when we have found the correct ones by numerical means we can also write down the roots of the quintic in terms of square roots, cube roots, and the Bring radical, which is therefore an algebraic solution in terms of algebraic functions of a single variable — an algebraic solution of the general quintic.
in 1858, and further methods later developed by other mathematicians.
and Leopold Kronecker
came upon equivalent solutions. Hermite arrived at this solution by generalizing the well-known solution to the cubic equation in terms of trigonometric function
s and finds the solution to a quintic in Bring–Jerrard form:
into which any quintic equation may be reduced by means of Tschirnhaus transformations as has been shown. He observed that elliptic function
s had an analogous role to play in the solution of the Bring–Jerrard quintic as the trigonometric functions had for the cubic. If
and 
are the periods of an elliptic integral
of the first kind: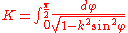
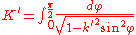
the elliptic nome is given by:
and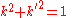
With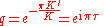
define the two elliptic modular functions: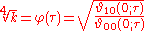
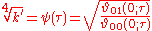
where
and similar are Jacobi theta functions.
If n is a prime number
, we can define two values u and v as follows:
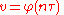
and
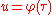
The parameters
and 
are linked by an equation of degree n + 1 known as the modular equation
, whose n + 1 roots are given by:
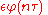
and
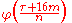
where ε is 1 or −1 depending on whether 2 is a quadratic residue with respect to n or not, and m is an integer modulo n. For n = 5, we have the modular equation of the sixth degree:
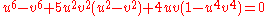
with six roots as shown above.
The modular equation of the sixth degree may be related to the Bring–Jerrard quintic by the following function of the six roots of the modular equation:
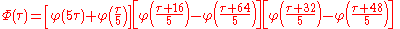
The five quantities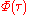
, 
, 
, 
, 
are the roots of a quintic equation with coefficients rational in 
:
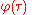which may be readily converted into the Bring–Jerrard form by the substitution:
leading to the Bring–Jerrard quintic:
where
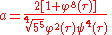
The Hermite–Kronecker–Brioschi method then amounts to finding a value for τ that corresponds to the value of a, and then using that value of τ to obtain the roots of the corresponding modular equation. To do this, let
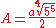
and calculate the required elliptic modulus
by solving the quartic equation:
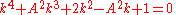
The roots of this equation are:
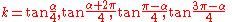
where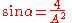
(note that some important references erroneously give it as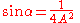 
). Any of these roots may be used as the elliptic modulus for the purposes of the method. The value of
may be easily obtained from the elliptic modulus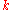 
by the relations given above. The roots of the Bring–Jerrard quintic are then given by: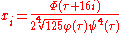
for
.
It may be seen that this process uses a generalization of the nth root
, which may be expressed as: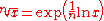
or more to the point, as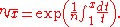
The Hermite–Kronecker–Brioschi method essentially replaces the exponential by an elliptic modular function, and the integral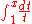
by an elliptic integral. Kronecker thought that this generalization was a special case of a still more general theorem, which would be applicable to equations of arbitrarily high degree. This theorem, known as Thomae's formula, was fully expressed by Hiroshi Umemura in 1984, who used Siegel modular form
s in place of the exponential/elliptic modular function, and the integral by a hyperelliptic integral.
equation of the form:
In particular, the quintic equation can be reduced to this form by the use of Tschirnhaus transformations as shown above. Let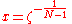
, the general form becomes:
where
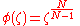
A formula due to Lagrange
states that for any analytic function
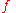, in the neighborhood of a root of the transformed general equation in terms of 
, above may be expressed as an infinite series:
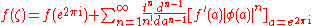
If we let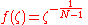
in this formula, we can come up with the root:
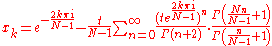
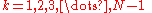
By the use of the Gauss multiplication theorem the infinite series above may be broken up into a finite series of hypergeometric functions:
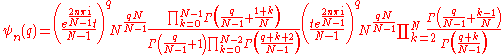
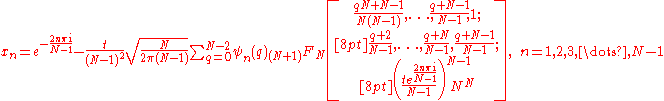
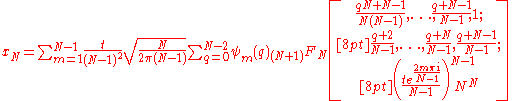
A root of the equation can thus be expressed as the sum of at most N − 1 hypergeometric functions. Applying this method to the reduced Bring–Jerrard quintic, define the following functions:
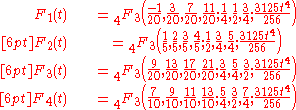
which are the hypergeometric functions that appear in the series formula above. The roots of the quintic are thus: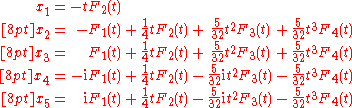
This is essentially the same result as that obtained by the method of differential resolvents developed by James Cockle and Robert Harley in 1860.
and a function
is to be determined such that:
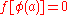
The function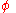
must also satisfy the following four differential equations:
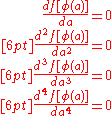
Expanding these and combining them together yields the differential resolvent:
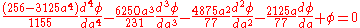
The solution of the differential resolvent, being a fourth order ordinary differential equation, depends on four constants of integration, which should be chosen so as to satisfy the original quintic. This is a Fuchsian ordinary differential equation of hypergeometric type, whose solution turns out to be identical to the series of hypergeometric functions that arose in Glasser's derivation above.
This method may also be generalized to equations of arbitrarily high degree, with differential resolvents which are partial differential equation
s, whose solutions involve hypergeometric functions of several variables.
A general formula for differential resolvents of arbitrary univariate polynomials is given by Nahay's powersum formula.
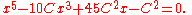
The iteration algorithm proceeds as follows:
1. Set
2. Compute the rational function
3. Iterate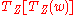
on a random starting guess until it converges. Call the limit point
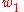and let 
.
4. Compute
5. Finally, compute
The two polynomial functions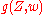
and 
are as follows:
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a Bring radical or ultraradical of a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
a is a root of the polynomial
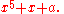
(The root is chosen so the radical of a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is real, and the radical is a differentiable function of a in the complex plane, with a branch cut along the negative real line below −1. See the "Bring radicals" section below.)
George Jerrard
George Jerrard
George Birch Jerrard was a British mathematician.He studied at Trinity College, Dublin from 1821 to 1827. His main work was on the theory of equations, where he was reluctant to accept the validity of the work of Niels Henrik Abel on the insolubility of the quintic equation by radicals...
(1804–1863) showed that some quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
s can be solved using radicals
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
and Bring radicals, which had been introduced by Erland Bring
Erland Samuel Bring
Erland Samuel Bring was a Swedish mathematician.Bring studied at Lund University between 1750 and 1757. In 1762 he obtained a position of a reader in history and was promoted to professor in 1779...
(1736–1798). They can be used to obtain closed-form solutions of quintic equations.
Normal forms
The quintic equation is rather difficult to obtain solutions for directly, with five independent coefficients in its most general form: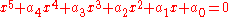The various methods for solving the quintic that have been developed generally attempt to simplify the quintic using Tschirnhaus transformation
Tschirnhaus transformation
In mathematics, a Tschirnhaus transformation, also known as Tschirnhausen transformation, is a type of mapping on polynomials developed by Ehrenfried Walther von Tschirnhaus in 1683. It may be defined conveniently by means of field theory, as the transformation on minimal polynomials implied by a...
s to reduce the number of independent coefficients.
Principal quintic form
The general quintic may be reduced into what is known as the principal quintic form, with the quartic and cubic terms removed: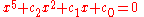If the roots of a general quintic and a principal quintic are related by a quadratic Tschirnhaus transformation:
the coefficients α and β may be determined by using the resultant, or by means of the power-sum formulae of the quintic roots. This leads to a system of equations in α and β consisting of a quadratic and a linear equation, and either of the two sets of solutions may be used to obtain the corresponding three coefficients of the principal quintic form.
This form is used by Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's solution to the quintic.
Bring–Jerrard normal form
It is possible to simplify the quintic still further and eliminate the quadratic term, producing the Bring–Jerrard normal form:Using the power-sum formulae again with a cubic transformation as Tschirnhaus
Ehrenfried Walther von Tschirnhaus
Ehrenfried Walther von Tschirnhaus was a German mathematician, physicist, physician, and philosopher...
tried does not work, since the resulting system of equations results in a sixth-degree equation.
In 1796 Bring
Erland Samuel Bring
Erland Samuel Bring was a Swedish mathematician.Bring studied at Lund University between 1750 and 1757. In 1762 he obtained a position of a reader in history and was promoted to professor in 1779...
found a way around this by using a quartic Tschirnhaus transformation to relate the roots of a principal quintic to those of a Bring–Jerrard quintic:
The extra parameter this fourth-order transformation provides allowed Bring to decrease the degrees of the other parameters. This leads to a system of five equations in six unknowns, which then requires the solution of a cubic and a quadratic equation. This method was also discovered by Jerrard
George Jerrard
George Birch Jerrard was a British mathematician.He studied at Trinity College, Dublin from 1821 to 1827. His main work was on the theory of equations, where he was reluctant to accept the validity of the work of Niels Henrik Abel on the insolubility of the quintic equation by radicals...
in 1852, but it is likely that he was unaware of Bring's previous work in this area. The full transformation may readily be accomplished using a computer algebra package such as Mathematica
Mathematica
Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
or Maple
Maple (software)
Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
. As might be expected from the complexity of these transformations, the resulting expressions can be enormous, particularly when compared to the solutions in radicals for lower degree equations, taking many megabytes of storage for a general quintic with symbolic coefficients.
Regarded as an algebraic function, the solutions to
involve two variables, d1 and d0, however the reduction is actually to an algebraic function of one variable, very much analogous to a solution in radicals, since we may further reduce the Bring–Jerrard form. If we for instance set
then we reduce the equation to the form
which involves z as an algebraic function of a single variable t, where
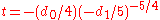. A similar transformation suffices to reduce the equation towhich is the form required by the Hermite-Kronecker-Brioschi method, Glasser's method, and the Cockle-Harley method of differential resolvents described below.
Brioschi normal form
There is another one-parameter normal form for the quintic equation, known as Brioschi normal form: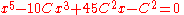which can be derived by using the following rational Tschirnhaus transformation
to relate the roots of a principal quintic to a Brioschi quintic. The values of the parameters
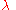and 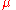may be derived by using polyhedral functions on the Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, and is related to the partition of an object of icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
into five objects of tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
.
It is to be noted that this Tschirnhaus transformation is rather simpler than the difficult one used to transform a principal quintic into Bring–Jerrard form. This normal form is used by the Doyle–McMullen iteration method and the Kiepert method.
Series representation
A Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for Bring radicals, as well as a representation in terms of hypergeometric functions can be derived as follows. The equation
can be rewritten as ; by setting 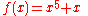, the desired solution is 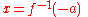.The series for
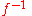can then be obtained by reversionLagrange inversion theorem
In mathematical analysis, the Lagrange inversion theorem, also known as the Lagrange-Bürmann formula, gives the Taylor series expansion of the inverse function of an analytic function.-Theorem statement:...
of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for
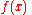(which is simply ), giving: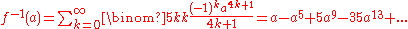where the absolute values of the coefficients are sequence A002294 in the OEIS
On-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
. The series confirms that
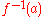is odd. This gives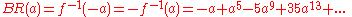The series converges for |z| < 1 and can be analytically continued in the complex plane. The above result can be written in hypergeometric form as:
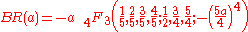
Compare with the hypergeometric functions that arise in Glasser's derivation and the method of differential resolvents below.
Solution of the general quintic
We now may express the roots of any polynomial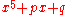in terms of the Bring radical as
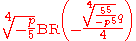
and its four conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
s. We have a reduction to the Bring–Jerrard form in terms of solvable polynomial equations, and we used transformations involving polynomial expressions in the roots only up to the fourth degree, which means inverting the transformation may be done by finding the roots of a polynomial solvable in radicals. This procedure produces extraneous solutions, but when we have found the correct ones by numerical means we can also write down the roots of the quintic in terms of square roots, cube roots, and the Bring radical, which is therefore an algebraic solution in terms of algebraic functions of a single variable — an algebraic solution of the general quintic.
Other characterizations
Many other characterizations of the Bring radical have been developed, the first of which is in terms of elliptic modular functions by Charles HermiteCharles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
in 1858, and further methods later developed by other mathematicians.
The Hermite–Kronecker–Brioschi characterization
In 1858, Charles Hermite published the first known solution to the general quintic equation in terms of elliptic transcendents, and at around the same time Francesco BrioschiFrancesco Brioschi
Francesco Brioschi was an Italian mathematician.Brioschi was born in Milan in 1824. From 1850 he taught analytical mechanics in the University of Pavia. After the Italian unification in 1861, he was elected depute in the Parliament of Italy and then appointed twice secretary of the Education...
and Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
came upon equivalent solutions. Hermite arrived at this solution by generalizing the well-known solution to the cubic equation in terms of trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s and finds the solution to a quintic in Bring–Jerrard form:
into which any quintic equation may be reduced by means of Tschirnhaus transformations as has been shown. He observed that elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s had an analogous role to play in the solution of the Bring–Jerrard quintic as the trigonometric functions had for the cubic. If
and are the periods of an elliptic integralElliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
of the first kind:
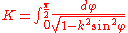
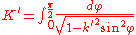
the elliptic nome is given by:
and
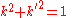
With
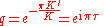
define the two elliptic modular functions:
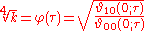
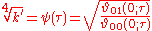
where
and similar are Jacobi theta functions.If n is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, we can define two values u and v as follows:
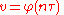
and
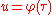
The parameters
and are linked by an equation of degree n + 1 known as the modular equationModular equation
In mathematics, a modular equation is an algebraic equation satisfied by moduli, in the sense of moduli problem. That is, given a number of functions on a moduli space, a modular equation is an equation holding between them, or in other words an identity for moduli.The most frequent use of the term...
, whose n + 1 roots are given by:
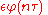
and
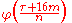
where ε is 1 or −1 depending on whether 2 is a quadratic residue with respect to n or not, and m is an integer modulo n. For n = 5, we have the modular equation of the sixth degree:
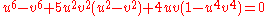
with six roots as shown above.
The modular equation of the sixth degree may be related to the Bring–Jerrard quintic by the following function of the six roots of the modular equation:
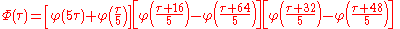
The five quantities
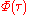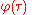, , , , are the roots of a quintic equation with coefficients rational in :which may be readily converted into the Bring–Jerrard form by the substitution:
leading to the Bring–Jerrard quintic:
where
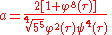
The Hermite–Kronecker–Brioschi method then amounts to finding a value for τ that corresponds to the value of a, and then using that value of τ to obtain the roots of the corresponding modular equation. To do this, let
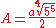
and calculate the required elliptic modulus
by solving the quartic equation: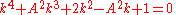The roots of this equation are:
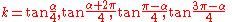
where
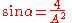(note that some important references erroneously give it as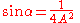 ). Any of these roots may be used as the elliptic modulus for the purposes of the method. The value of
may be easily obtained from the elliptic modulus 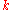by the relations given above. The roots of the Bring–Jerrard quintic are then given by: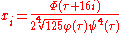for
.It may be seen that this process uses a generalization of the nth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, which may be expressed as:
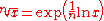
or more to the point, as
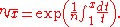
The Hermite–Kronecker–Brioschi method essentially replaces the exponential by an elliptic modular function, and the integral
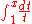by an elliptic integral. Kronecker thought that this generalization was a special case of a still more general theorem, which would be applicable to equations of arbitrarily high degree. This theorem, known as Thomae's formula, was fully expressed by Hiroshi Umemura in 1984, who used Siegel modular formSiegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
s in place of the exponential/elliptic modular function, and the integral by a hyperelliptic integral.
Glasser's derivation
This derivation due to M. L. Glasser generalizes the series method presented earlier in this article to find a solution to any trinomialTrinomial
In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials.-Trinomial expressions:# 3x + 5y + 8z with x, y, z variables# 3t + 9s^2 + 3y^3 with t, s, y variables# 3ts + 9t + 5s with t, s variables...
equation of the form:
In particular, the quintic equation can be reduced to this form by the use of Tschirnhaus transformations as shown above. Let
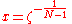, the general form becomes:where
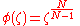
A formula due to Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
states that for any analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
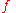, in the neighborhood of a root of the transformed general equation in terms of , above may be expressed as an infinite series: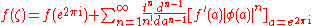If we let
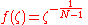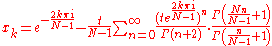
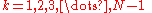
in this formula, we can come up with the root:By the use of the Gauss multiplication theorem the infinite series above may be broken up into a finite series of hypergeometric functions:
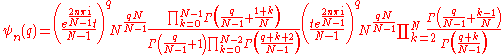
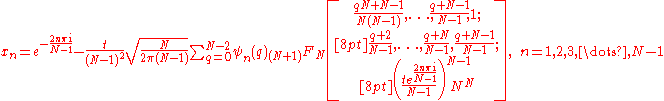
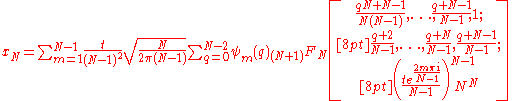
A root of the equation can thus be expressed as the sum of at most N − 1 hypergeometric functions. Applying this method to the reduced Bring–Jerrard quintic, define the following functions:
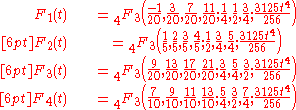
which are the hypergeometric functions that appear in the series formula above. The roots of the quintic are thus:
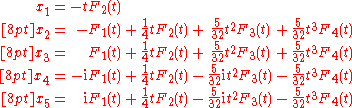
This is essentially the same result as that obtained by the method of differential resolvents developed by James Cockle and Robert Harley in 1860.
The method of differential resolvents
James Cockle and Robert Harley developed a method for solving the quintic by means of differential equations. They consider the roots as being functions of the coefficients, and calculate a differential resolvent based on these equations. The Bring–Jerrard quintic is expressed as a function:and a function
is to be determined such that: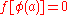The function
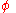must also satisfy the following four differential equations: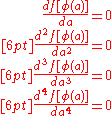Expanding these and combining them together yields the differential resolvent:
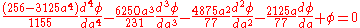
The solution of the differential resolvent, being a fourth order ordinary differential equation, depends on four constants of integration, which should be chosen so as to satisfy the original quintic. This is a Fuchsian ordinary differential equation of hypergeometric type, whose solution turns out to be identical to the series of hypergeometric functions that arose in Glasser's derivation above.
This method may also be generalized to equations of arbitrarily high degree, with differential resolvents which are partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, whose solutions involve hypergeometric functions of several variables.
A general formula for differential resolvents of arbitrary univariate polynomials is given by Nahay's powersum formula.
Doyle–McMullen iteration
In 1989, Peter Doyle and Curt McMullen derived an iteration method that solves a quintic in Brioschi normal form: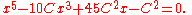The iteration algorithm proceeds as follows:
1. Set
2. Compute the rational function
-
-
- where
is a polynomial function given below, and 
is the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of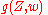
with respect to 
3. Iterate
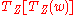on a random starting guess until it converges. Call the limit pointLimit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
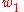and let .4. Compute
-
- where
is a polynomial function given below. Do this for both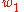 
and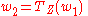 
.
5. Finally, compute
-
- for i = 1, 2. These are two of the roots of the Brioschi quintic.
The two polynomial functions
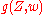and are as follows:-
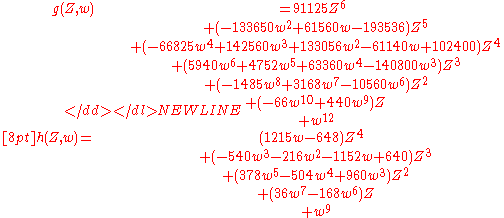
This iteration method produces two roots of the quintic. The remaining three roots can be obtained by using synthetic divisionSynthetic divisionSynthetic division is a method of performing polynomial long division, with less writing and fewer calculations. It is mostly taught for division by binomials of the formx - a,\ but the method generalizes to division by any monic polynomial...
to divide the two roots out, producing a cubic equation. It is to be noted that due to the way the iteration is formulated, this method seems to always find two complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
roots of the quintic even when all the quintic coefficients are real and the starting guess is real. This iteration method is derived by from the symmetries of the icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
and is closely related to the method Felix Klein describes in his book.