
Clifford bundle
Encyclopedia
In mathematics
, a Clifford bundle is an algebra bundle
whose fibers have the structure of a Clifford algebra
and whose local trivializations respect the algebra structure. There is a natural Clifford bundle associated to any (pseudo
) Riemannian manifold
M which is called the Clifford bundle of M.
or complex
) vector space
together with a symmetric bilinear form
<·,·>. The Clifford algebra
Cℓ(V) is a natural (unital associative
) algebra
generated by V subject only to the relation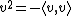
for all v in V. One can construct Cℓ(V) as a quotient of the tensor algebra
of V by the ideal
generated by the above relation.
Like other tensor operations, this construction can be carried out fiberwise on a smooth vector bundle
. Let E be a smooth vector bundle over a smooth manifold M, and let g be a smooth symmetric bilinear form on E. The Clifford bundle of E is the fiber bundle
whose fibers are the Clifford algebras generated by the fibers of E: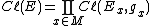
The topology of Cℓ(E) is determined by that of E via an associated bundle
construction.
One is most often interested in the case where g is positive-definite or at least nondegenerate; that is, when (E, g) is a Riemannian or pseudo-Riemannian vector bundle. For concreteness, suppose that (E, g) is a Riemannian vector bundle. The Clifford bundle of E can be constructed as follows. Let CℓnR be the Clifford algebra generated by Rn with the Euclidean metric. The standard action of the orthogonal group
O(n) on Rn induces a graded automorphism
of CℓnR. The homomorphism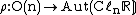
is determined by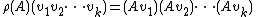
where vi are all vectors in Rn. The Clifford bundle of E is then given by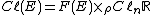
where F(E) is the orthonormal frame bundle of E. It is clear from this construction that the structure group of Cℓ(E) is O(n). Since O(n) acts by graded automorphisms on CℓnR it follows that Cℓ(E) is a bundle of Z2-graded algebras
over M. The Clifford bundle Cℓ(E) can then be decomposed into even and odd subbundles: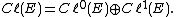
If the vector bundle E is orientable
then one can reduce the structure group of Cℓ(E) from O(n) to SO(n) in the natural manner.
with metric
g, then the Clifford bundle of M is the Clifford bundle generated by the tangent bundle
TM. One can also build a Clifford bundle out of the cotangent bundle
T*M. The metric induces a natural isomorphism TM = T*M and therefore an isomorphism Cℓ(TM) = Cℓ(T*M).
There is a natural vector bundle isomorphism between the Clifford bundle of M and the exterior bundle
of M: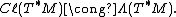
This is an isomorphism of vector bundles not algebra bundles. The isomorphism is induced from the corresponding isomorphism on each fiber. In this way one can think of sections of the Clifford bundle as differential form
s on M equipped with Clifford multiplication rather than the wedge product (which is independent of the metric).
The above isomorphism respects the grading in the sense that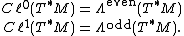
Let M be an n-dimensional spin manifold with spin structure
FSpin(M) → FSO(M) on M. Given any CℓnR-module V one can construct the associated spinor bundle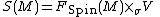
where σ : Spin(n) → GL(V) is the representation of Spin(n) given by left multiplication on S. Such a spinor bundle is said to be real, complex, graded or ungraded according to whether on not V has the corresponding property. Sections of S(M) are called spinor
s on M.
Given a spinor bundle S(M) there is a natural bundle map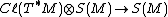
which is given by left multiplication on each fiber. The spinor bundle S(M) is therefore a bundle of Clifford modules over Cℓ(T*M).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Clifford bundle is an algebra bundle
Algebra bundle
In mathematics, an algebra bundle is a fiber bundle whose fibers are algebras and local trivializations respect the algebra structure. It follows that the transition functions are algebra isomorphisms...
whose fibers have the structure of a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
and whose local trivializations respect the algebra structure. There is a natural Clifford bundle associated to any (pseudo
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
) Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
M which is called the Clifford bundle of M.
General construction
Let V be a (realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
together with a symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
<·,·>. The Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
Cℓ(V) is a natural (unital associative
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
) algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
generated by V subject only to the relation
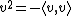
for all v in V. One can construct Cℓ(V) as a quotient of the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
of V by the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the above relation.
Like other tensor operations, this construction can be carried out fiberwise on a smooth vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
. Let E be a smooth vector bundle over a smooth manifold M, and let g be a smooth symmetric bilinear form on E. The Clifford bundle of E is the fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
whose fibers are the Clifford algebras generated by the fibers of E:
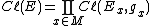
The topology of Cℓ(E) is determined by that of E via an associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
construction.
One is most often interested in the case where g is positive-definite or at least nondegenerate; that is, when (E, g) is a Riemannian or pseudo-Riemannian vector bundle. For concreteness, suppose that (E, g) is a Riemannian vector bundle. The Clifford bundle of E can be constructed as follows. Let CℓnR be the Clifford algebra generated by Rn with the Euclidean metric. The standard action of the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n) on Rn induces a graded automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of CℓnR. The homomorphism
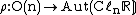
is determined by
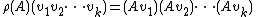
where vi are all vectors in Rn. The Clifford bundle of E is then given by
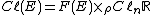
where F(E) is the orthonormal frame bundle of E. It is clear from this construction that the structure group of Cℓ(E) is O(n). Since O(n) acts by graded automorphisms on CℓnR it follows that Cℓ(E) is a bundle of Z2-graded algebras
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
over M. The Clifford bundle Cℓ(E) can then be decomposed into even and odd subbundles:
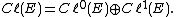
If the vector bundle E is orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
then one can reduce the structure group of Cℓ(E) from O(n) to SO(n) in the natural manner.
Clifford bundle of a Riemannian manifold
If M is a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
g, then the Clifford bundle of M is the Clifford bundle generated by the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM. One can also build a Clifford bundle out of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T*M. The metric induces a natural isomorphism TM = T*M and therefore an isomorphism Cℓ(TM) = Cℓ(T*M).
There is a natural vector bundle isomorphism between the Clifford bundle of M and the exterior bundle
Exterior bundle
In mathematics, the exterior bundle of a manifold M is the subbundle of the tensor bundle consisting of all antisymmetric covariant tensors. It has special significance, because one can define a connection-independent derivative on it, namely the exterior derivative.Sections of the exterior bundle...
of M:
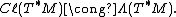
This is an isomorphism of vector bundles not algebra bundles. The isomorphism is induced from the corresponding isomorphism on each fiber. In this way one can think of sections of the Clifford bundle as differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on M equipped with Clifford multiplication rather than the wedge product (which is independent of the metric).
The above isomorphism respects the grading in the sense that
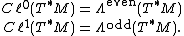
Spinor bundles
Given an oriented Riemannian manifold M one can ask whether it is possible to construct a bundle of irreducible Clifford modules over Cℓ(T*M). In fact, such a bundle can be constructed if and only if M is a spin manifold.Let M be an n-dimensional spin manifold with spin structure
Spin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
FSpin(M) → FSO(M) on M. Given any CℓnR-module V one can construct the associated spinor bundle
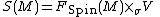
where σ : Spin(n) → GL(V) is the representation of Spin(n) given by left multiplication on S. Such a spinor bundle is said to be real, complex, graded or ungraded according to whether on not V has the corresponding property. Sections of S(M) are called spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s on M.
Given a spinor bundle S(M) there is a natural bundle map
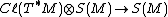
which is given by left multiplication on each fiber. The spinor bundle S(M) is therefore a bundle of Clifford modules over Cℓ(T*M).

