
Decisional Diffie-Hellman assumption
Encyclopedia
The decisional Diffie–Hellman (DDH) assumption is a computational hardness assumption about a certain problem involving discrete logarithm
s in cyclic group
s. It is used as the basis to prove the security of many cryptographic
protocols, most notably the ElGamal
and Cramer–Shoup cryptosystems.
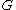 of order
of order 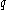 , and with generator
, and with generator
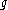 . The DDH assumption states that, given
. The DDH assumption states that, given 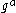 and
and 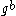 for randomly-chosen
for randomly-chosen 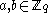 , the value
, the value 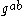 "looks like" a random element in
"looks like" a random element in 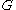 .
.
This intuitive notion is formally stated by saying that the following two probability distributions are computationally indistinguishable (in the security parameter
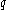 ):
):
Triples of the first kind are often called DDH triples or DDH tuples.
. If it were possible to efficiently compute discrete logs in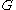 , then the DDH assumption would not hold in
, then the DDH assumption would not hold in 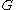 . Given
. Given 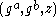 , one could efficiently decide whether
, one could efficiently decide whether 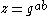 by first taking the discrete log
by first taking the discrete log  of
of 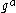 , and then comparing
, and then comparing  with
with 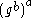 .
.
For this reason, DDH is considered a stronger assumption than discrete log, in the following sense: there are groups for which detecting DDH tuples is easy, but computing discrete logs is believed to be hard. Thus, requiring that the DDH assumption holds in a group is a more restricting requirement.
The DDH assumption is also related to the computational Diffie–Hellman assumption (CDH). If it were possible to efficiently compute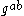 from
from 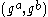 , then one could easily distinguish the two probability distributions above. Similar to above, DDH is considered a stronger assumption than CDH.
, then one could easily distinguish the two probability distributions above. Similar to above, DDH is considered a stronger assumption than CDH.
, meaning, roughly, that if it is hard for even a small fraction of inputs, it is hard for almost all inputs; if it is easy for even a small fraction of inputs, it is easy for almost all inputs.
Importantly, the DDH assumption does not hold in the multiplicative group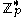 , where
, where 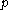 is prime. This is because given
is prime. This is because given 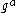 and
and 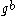 , one can efficiently compute the Legendre symbol
, one can efficiently compute the Legendre symbol
of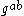 , giving a successful method to distinguish
, giving a successful method to distinguish 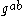 from a random group element.
from a random group element.
The DDH assumption does not hold on elliptic curves over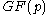 with small embedding degree (say, less than
with small embedding degree (say, less than 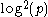 ), a class which includes supersingular elliptic curves. This is because the Weil pairing
), a class which includes supersingular elliptic curves. This is because the Weil pairing
or Tate pairing can be used to solve the problem directly as follows: given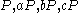 on such a curve, one can compute
on such a curve, one can compute 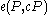 and
and 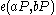 . By the bilinearity of the pairings, the two expressions are equal if and only if
. By the bilinearity of the pairings, the two expressions are equal if and only if 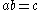 modulo the order of
modulo the order of 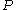 . If the embedding degree is large (say around the size of
. If the embedding degree is large (say around the size of 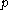 ) then the DDH assumption will still hold because the pairing cannot be computed. Even if the embedding degree is small, there are some subgroups of the curve in which the DDH assumption is believed to hold.
) then the DDH assumption will still hold because the pairing cannot be computed. Even if the embedding degree is small, there are some subgroups of the curve in which the DDH assumption is believed to hold.
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
s in cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s. It is used as the basis to prove the security of many cryptographic
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
protocols, most notably the ElGamal
ElGamal encryption
In cryptography, the ElGamal encryption system is an asymmetric key encryption algorithm for public-key cryptography which is based on the Diffie–Hellman key exchange. It was described by Taher Elgamal in 1984. ElGamal encryption is used in the free GNU Privacy Guard software, recent versions of...
and Cramer–Shoup cryptosystems.
Definition
Consider a (multiplicative) cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
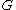 of order
of order 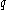 , and with generator
, and with generatorGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
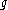 . The DDH assumption states that, given
. The DDH assumption states that, given 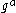 and
and 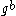 for randomly-chosen
for randomly-chosen 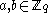 , the value
, the value 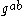 "looks like" a random element in
"looks like" a random element in 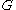 .
.This intuitive notion is formally stated by saying that the following two probability distributions are computationally indistinguishable (in the security parameter
Security parameter
In cryptography, the security parameter is a variable that measures the input size of the problem. Both the resource requirements of the cryptographic algorithm or protocol as well as the adversary's probability of breaking security are expressed in terms of the security parameter.The security...
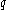 ):
):
-
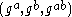 , where
, where  and
and 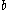 are randomly and independently chosen from
are randomly and independently chosen from 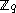 .
. -
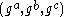 , where
, where 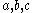 are randomly and independently chosen from
are randomly and independently chosen from 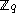 .
.
Triples of the first kind are often called DDH triples or DDH tuples.
Relation to other assumptions
The DDH assumption is related to the discrete log assumptionDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
. If it were possible to efficiently compute discrete logs in
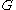 , then the DDH assumption would not hold in
, then the DDH assumption would not hold in 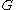 . Given
. Given 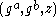 , one could efficiently decide whether
, one could efficiently decide whether 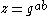 by first taking the discrete log
by first taking the discrete log  of
of 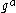 , and then comparing
, and then comparing  with
with 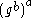 .
.For this reason, DDH is considered a stronger assumption than discrete log, in the following sense: there are groups for which detecting DDH tuples is easy, but computing discrete logs is believed to be hard. Thus, requiring that the DDH assumption holds in a group is a more restricting requirement.
The DDH assumption is also related to the computational Diffie–Hellman assumption (CDH). If it were possible to efficiently compute
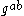 from
from 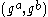 , then one could easily distinguish the two probability distributions above. Similar to above, DDH is considered a stronger assumption than CDH.
, then one could easily distinguish the two probability distributions above. Similar to above, DDH is considered a stronger assumption than CDH.Other properties
The problem of detecting DDH tuples is random self-reducibleRandom Self-reducibility
Random self-reducibility is the rule that a good algorithm for the average case implies a good algorithm for the worst case. RSR is the ability to solve all instances of a problem by solving a large fraction of the instances.-Definition:...
, meaning, roughly, that if it is hard for even a small fraction of inputs, it is hard for almost all inputs; if it is easy for even a small fraction of inputs, it is easy for almost all inputs.
Groups for which DDH is assumed to hold
When using a cryptographic protocol whose security depends on the DDH assumption, it is important that the protocol is implemented using groups where DDH is believed to hold:- The subgroup of
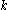 th residues modulo a prime
th residues modulo a prime 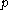 , where
, where 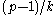 is also a large prime (also called a Schnorr group). For the case of
is also a large prime (also called a Schnorr group). For the case of 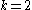 , this corresponds to the group of quadratic residues modulo a safe primeSafe primeA safe prime is a prime number of the form 2p + 1, where p is also a prime. The first few safe primes are...
, this corresponds to the group of quadratic residues modulo a safe primeSafe primeA safe prime is a prime number of the form 2p + 1, where p is also a prime. The first few safe primes are...
.
- The cyclic group of order
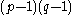 , where
, where 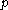 and
and 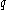 are safe primeSafe primeA safe prime is a prime number of the form 2p + 1, where p is also a prime. The first few safe primes are...
are safe primeSafe primeA safe prime is a prime number of the form 2p + 1, where p is also a prime. The first few safe primes are...
s.
- A prime-order elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
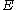 over the fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
over the fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
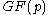 , where
, where 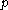 is prime, provided
is prime, provided 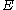 has large embedding degree.
has large embedding degree.
- A JacobianJacobianIn vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of a hyper-elliptic curve over the fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
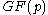 with a prime number of reduced divisors, where
with a prime number of reduced divisors, where 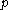 is prime, provided the Jacobian has large embedding degree.
is prime, provided the Jacobian has large embedding degree.
Importantly, the DDH assumption does not hold in the multiplicative group
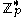 , where
, where 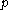 is prime. This is because given
is prime. This is because given 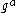 and
and 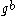 , one can efficiently compute the Legendre symbol
, one can efficiently compute the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
of
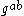 , giving a successful method to distinguish
, giving a successful method to distinguish 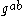 from a random group element.
from a random group element.The DDH assumption does not hold on elliptic curves over
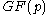 with small embedding degree (say, less than
with small embedding degree (say, less than 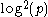 ), a class which includes supersingular elliptic curves. This is because the Weil pairing
), a class which includes supersingular elliptic curves. This is because the Weil pairingWeil pairing
In mathematics, the Weil pairing is a construction of roots of unity by means of functions on an elliptic curve E, in such a way as to constitute a pairing on the torsion subgroup of E...
or Tate pairing can be used to solve the problem directly as follows: given
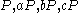 on such a curve, one can compute
on such a curve, one can compute 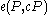 and
and 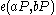 . By the bilinearity of the pairings, the two expressions are equal if and only if
. By the bilinearity of the pairings, the two expressions are equal if and only if 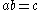 modulo the order of
modulo the order of 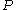 . If the embedding degree is large (say around the size of
. If the embedding degree is large (say around the size of 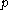 ) then the DDH assumption will still hold because the pairing cannot be computed. Even if the embedding degree is small, there are some subgroups of the curve in which the DDH assumption is believed to hold.
) then the DDH assumption will still hold because the pairing cannot be computed. Even if the embedding degree is small, there are some subgroups of the curve in which the DDH assumption is believed to hold.See also
- Diffie–Hellman problem
- Diffie–Hellman key exchange
- Computational hardness assumptionsComputational hardness assumptionsIn cryptography, a major goal is to create cryptographic primitives with provable security. In some cases cryptographic protocols are found to have information theoretic security, the one-time pad is a common example. In many cases, information theoretic security cannot be achieved, and in such...
- XDH assumptionXDH AssumptionThe external Diffie–Hellman assumption is a mathematic assumption used in elliptic curve cryptography. The XDH assumption holds that there exist certain subgroups of elliptic curves which have useful properties for cryptography...
- Decisional Linear assumptionDecisional Linear assumptionThe Decision Linear assumption is a mathematical assumption used in elliptic curve cryptography. In particular, the DLIN assumption is useful in settings where the decisional Diffie–Hellman assumption does not hold...

