
Differential calculus over commutative algebras
Encyclopedia
In mathematics
the differential calculus over commutative algebras is a part of commutative algebra
based on the observation that most concepts known from classical differential calculus
can be formulated in purely algebraic terms. Instances of this are:
Denoting the set of kth order linear differential operators from an -module
-module 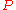 to an
to an  -module
-module  with
with 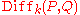 we obtain a bi-functor with values in the category
we obtain a bi-functor with values in the category
of -modules. Other natural concepts of calculus such as jet spaces, differential form
-modules. Other natural concepts of calculus such as jet spaces, differential form
s are then obtained as representing object
s of the functors and related functors.
and related functors.
Seen from this point of view calculus may in fact be understood as the theory of these functors and their representing objects.
Replacing the real numbers with any commutative ring
with any commutative ring
, and the algebra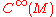 with any commutative algebra the above said remains meaningful, hence differential calculus can be developed for arbitrary commutative algebras. Many of these concepts are widely used in algebraic geometry
with any commutative algebra the above said remains meaningful, hence differential calculus can be developed for arbitrary commutative algebras. Many of these concepts are widely used in algebraic geometry
, differential geometry and secondary calculus
. Moreover the theory generalizes naturally to the setting of graded commutative algebra
, allowing for a natural foundation of calculus on supermanifold
s, graded manifold
s and associated concepts like the Berezin integral
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the differential calculus over commutative algebras is a part of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
based on the observation that most concepts known from classical differential calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
can be formulated in purely algebraic terms. Instances of this are:
- The whole topological information of a smooth manifold
 is encoded in the algebraic properties of its
is encoded in the algebraic properties of its  -algebraAlgebra (ring theory)In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
-algebraAlgebra (ring theory)In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
of smooth functions as in the Banach–Stone theorem.
as in the Banach–Stone theorem. - Vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s over correspond to projective finitely generated moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
correspond to projective finitely generated moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over , via the functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
, via the functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
 which associates to a vector bundle its module of sections.
which associates to a vector bundle its module of sections. - Vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s on are naturally identified with derivationDerivation (abstract algebra)In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
are naturally identified with derivationDerivation (abstract algebra)In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
s of the algebra .
. - More generally, a linear differential operator of order k, sending sections of a vector bundle
 to sections of another bundle
to sections of another bundle  is seen to be an
is seen to be an  -linear map
-linear map 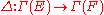 between the associated modules, such that for any k + 1 elements
between the associated modules, such that for any k + 1 elements 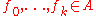 :
:

where the bracket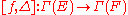 is defined as the commutator
is defined as the commutator

Denoting the set of kth order linear differential operators from an
 -module
-module 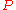 to an
to an  -module
-module  with
with 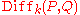 we obtain a bi-functor with values in the category
we obtain a bi-functor with values in the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of
 -modules. Other natural concepts of calculus such as jet spaces, differential form
-modules. Other natural concepts of calculus such as jet spaces, differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s are then obtained as representing object
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
s of the functors
 and related functors.
and related functors.Seen from this point of view calculus may in fact be understood as the theory of these functors and their representing objects.
Replacing the real numbers
 with any commutative ring
with any commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, and the algebra
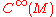 with any commutative algebra the above said remains meaningful, hence differential calculus can be developed for arbitrary commutative algebras. Many of these concepts are widely used in algebraic geometry
with any commutative algebra the above said remains meaningful, hence differential calculus can be developed for arbitrary commutative algebras. Many of these concepts are widely used in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, differential geometry and secondary calculus
Secondary calculus and cohomological physics
In mathematics, secondary calculus is a proposed expansion of classical differential calculus on manifolds, to the "space" of solutions of a partial differential equation...
. Moreover the theory generalizes naturally to the setting of graded commutative algebra
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
, allowing for a natural foundation of calculus on supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
s, graded manifold
Graded manifold
Graded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
s and associated concepts like the Berezin integral
Berezin integral
In mathematical physics, a Grassmann integral, or, more correctly, Berezin integral, is a way to define integration for functions of Grassmann variables. It is not an integral in the Lebesgue sense; it is called integration because it has analogous properties and since it is used in physics as a...
.

