
Graded manifold
Encyclopedia
Graded manifolds are extensions of the manifold
concept based on ideas coming from supersymmetry
and supercommutative algebra
. Graded manifolds are not supermanifold
s though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and supermanifolds are phrased in terms of sheaves
of graded commutative algebras
. However, graded manifolds are characterized by sheaves on smooth manifolds, while supermanifolds are constructed by gluing of sheaves of supervector spaces.
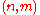 is defined as a locally ringed space
is defined as a locally ringed space  where
where  is an
is an  -dimensional smooth manifold
-dimensional smooth manifold
and is a
is a 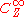 -sheaf of Grassmann algebras
-sheaf of Grassmann algebras
of rank where
where 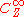 is the sheaf of smooth real functions on
is the sheaf of smooth real functions on  . A sheaf
. A sheaf  is called the structure sheaf of a graded manifold
is called the structure sheaf of a graded manifold 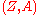 , and a manifold
, and a manifold  is said to be the body of
is said to be the body of  . Sections of the sheaf
. Sections of the sheaf  are called graded functions on a graded manifold
are called graded functions on a graded manifold 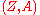 . They make up a graded commutative
. They make up a graded commutative 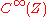 -ring
-ring 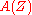 called the structure ring of
called the structure ring of 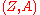 . The well-known Batchelor theorem and Serre-Swan theorem characterize graded manifolds as follows.
. The well-known Batchelor theorem and Serre-Swan theorem characterize graded manifolds as follows.
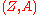 be a graded manifold. There exists a vector bundle
be a graded manifold. There exists a vector bundle
 with an
with an  -dimensional typical fiber
-dimensional typical fiber  such that the structure sheaf
such that the structure sheaf  of
of 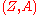 is isomorphic to the structure sheaf of sections of the exterior product
is isomorphic to the structure sheaf of sections of the exterior product 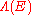 of
of  , whose typical fibre is the Grassmann algebra
, whose typical fibre is the Grassmann algebra 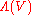 .
.
Let be a smooth manifold. A graded commutative
be a smooth manifold. A graded commutative 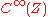 -algebra is isomorphic to the structure ring of a graded manifold with a body
-algebra is isomorphic to the structure ring of a graded manifold with a body  if and only if it is the exterior algebra
if and only if it is the exterior algebra
of some projective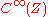 -module of finite rank.
-module of finite rank.
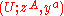 of the vector bundle
of the vector bundle  yields a splitting domain
yields a splitting domain 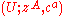 of a graded manifold
of a graded manifold 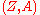 , where
, where 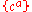 is the fiber basis for
is the fiber basis for  . Graded functions on such a chart are
. Graded functions on such a chart are 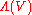 -valued functions
-valued functions
 ,
,
where are smooth real functions on
are smooth real functions on  and
and  are odd generating elements of the Grassmann algebra
are odd generating elements of the Grassmann algebra  .
.
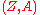 , graded derivations
, graded derivations
of the structure ring of graded functions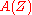 are called graded vector fields on
are called graded vector fields on 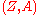 . They constitute a real Lie superalgebra
. They constitute a real Lie superalgebra
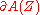 with respect to the superbracket
with respect to the superbracket
 ,
,
where denotes the Grassmann parity of
denotes the Grassmann parity of 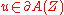 . Graded vector fields locally read
. Graded vector fields locally read
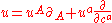 .
.
They act on graded functions by the rule
by the rule
 .
.
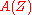 -dual of the module graded vector fields
-dual of the module graded vector fields  is called the module of graded exterior one-forms
is called the module of graded exterior one-forms 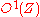 . Graded exterior one-forms locally read
. Graded exterior one-forms locally read 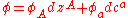 so that the duality (interior) product
so that the duality (interior) product
between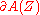 and
and 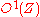 takes the form
takes the form
 .
.
Provided with the graded exterior product
 ,
,
graded one-forms generate the graded exterior algebra of graded exterior forms on a graded manifold. They obey the relation
of graded exterior forms on a graded manifold. They obey the relation
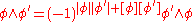 ,
,
where denotes the form degree of
denotes the form degree of  . The graded exterior algebra
. The graded exterior algebra  is a graded differential algebra with respect to the graded exterior differential
is a graded differential algebra with respect to the graded exterior differential
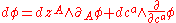 ,
,
where the graded derivations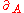 ,
,  are graded commutative with the graded forms
are graded commutative with the graded forms  and
and 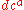 . There are
. There are
the familiar relations
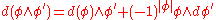 .
.
s of graded
manifolds, but they differ from jets of graded bundles.
similarly to the differential calculus over commutative algebras
.
fields on a smooth manifold are described in terms of graded
manifolds. Extended to graded manifolds, the variational bicomplex
provides the strict mathematical formulation of
Lagrangian classical field theory
and Lagrangian BRST theory.
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
concept based on ideas coming from supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
and supercommutative algebra
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
. Graded manifolds are not supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
s though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and supermanifolds are phrased in terms of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of graded commutative algebras
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
. However, graded manifolds are characterized by sheaves on smooth manifolds, while supermanifolds are constructed by gluing of sheaves of supervector spaces.
Graded manifolds
A graded manifold of dimension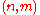 is defined as a locally ringed space
is defined as a locally ringed space  where
where  is an
is an  -dimensional smooth manifold
-dimensional smooth manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
and
 is a
is a 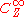 -sheaf of Grassmann algebras
-sheaf of Grassmann algebrasExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of rank
 where
where 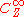 is the sheaf of smooth real functions on
is the sheaf of smooth real functions on  . A sheaf
. A sheaf  is called the structure sheaf of a graded manifold
is called the structure sheaf of a graded manifold 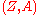 , and a manifold
, and a manifold  is said to be the body of
is said to be the body of  . Sections of the sheaf
. Sections of the sheaf  are called graded functions on a graded manifold
are called graded functions on a graded manifold 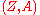 . They make up a graded commutative
. They make up a graded commutative 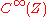 -ring
-ring 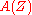 called the structure ring of
called the structure ring of 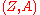 . The well-known Batchelor theorem and Serre-Swan theorem characterize graded manifolds as follows.
. The well-known Batchelor theorem and Serre-Swan theorem characterize graded manifolds as follows.Theorem
Let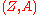 be a graded manifold. There exists a vector bundle
be a graded manifold. There exists a vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
 with an
with an  -dimensional typical fiber
-dimensional typical fiber  such that the structure sheaf
such that the structure sheaf  of
of 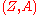 is isomorphic to the structure sheaf of sections of the exterior product
is isomorphic to the structure sheaf of sections of the exterior product 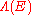 of
of  , whose typical fibre is the Grassmann algebra
, whose typical fibre is the Grassmann algebra 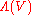 .
.Let
 be a smooth manifold. A graded commutative
be a smooth manifold. A graded commutative 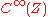 -algebra is isomorphic to the structure ring of a graded manifold with a body
-algebra is isomorphic to the structure ring of a graded manifold with a body  if and only if it is the exterior algebra
if and only if it is the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of some projective
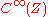 -module of finite rank.
-module of finite rank.Graded functions
Note that above mentioned Batchelor's isomorphism fails to be canonical, but it often is fixed from the beginning. In this case, every trivialization chart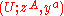 of the vector bundle
of the vector bundle  yields a splitting domain
yields a splitting domain 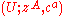 of a graded manifold
of a graded manifold 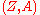 , where
, where 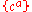 is the fiber basis for
is the fiber basis for  . Graded functions on such a chart are
. Graded functions on such a chart are 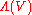 -valued functions
-valued functions ,
,where
 are smooth real functions on
are smooth real functions on  and
and  are odd generating elements of the Grassmann algebra
are odd generating elements of the Grassmann algebra  .
.Graded vector fields
Given a graded manifold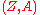 , graded derivations
, graded derivationsDifferential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
of the structure ring of graded functions
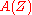 are called graded vector fields on
are called graded vector fields on 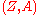 . They constitute a real Lie superalgebra
. They constitute a real Lie superalgebraLie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
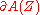 with respect to the superbracket
with respect to the superbracketLie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
 ,
,where
 denotes the Grassmann parity of
denotes the Grassmann parity of 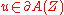 . Graded vector fields locally read
. Graded vector fields locally read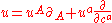 .
.They act on graded functions
 by the rule
by the rule .
.Graded exterior forms
The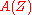 -dual of the module graded vector fields
-dual of the module graded vector fields  is called the module of graded exterior one-forms
is called the module of graded exterior one-forms 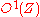 . Graded exterior one-forms locally read
. Graded exterior one-forms locally read 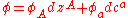 so that the duality (interior) product
so that the duality (interior) productbetween
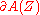 and
and 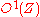 takes the form
takes the form .
.Provided with the graded exterior product
 ,
,graded one-forms generate the graded exterior algebra
 of graded exterior forms on a graded manifold. They obey the relation
of graded exterior forms on a graded manifold. They obey the relation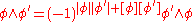 ,
,where
 denotes the form degree of
denotes the form degree of  . The graded exterior algebra
. The graded exterior algebra  is a graded differential algebra with respect to the graded exterior differential
is a graded differential algebra with respect to the graded exterior differential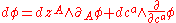 ,
,where the graded derivations
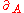 ,
,  are graded commutative with the graded forms
are graded commutative with the graded forms  and
and 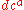 . There are
. There arethe familiar relations
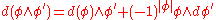 .
.Graded differential geometry
In the category of graded manifolds, one considers graded Lie groups, graded bundles and graded principal bundles. One also introduces the notion of jetJet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
s of graded
manifolds, but they differ from jets of graded bundles.
Graded differential calculus
The differential calculus on graded manifolds is formulated as the differential calculus over graded commutative algebrasSupercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
similarly to the differential calculus over commutative algebras
Differential calculus over commutative algebras
In mathematics the differential calculus over commutative algebras is a part of commutative algebra based on the observation that most concepts known from classical differential calculus can be formulated in purely algebraic terms...
.
Physical outcome
Due to the above mentioned Serre-Swan theorem, odd classicalfields on a smooth manifold are described in terms of graded
manifolds. Extended to graded manifolds, the variational bicomplex
Variational bicomplex
In mathematics, the Lagrangian theory on fiber bundles is globally formulated in algebraic terms of the variational bicomplex, without appealing to the calculus of variations...
provides the strict mathematical formulation of
Lagrangian classical field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
and Lagrangian BRST theory.
See also
- SupermanifoldSupermanifoldIn physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
- SupergeometrySupergeometrySupergeometry is differential geometry of modules over graded commutative algebras, supermanifolds and graded manifolds. Supergeometry is part and parcel of many classical and quantum field theories involving odd fields, e.g., SUSY field theory, BRST theory, or supergravity.Supergeometry is...
- SupersymmetrySupersymmetryIn particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
- Connection (algebraic framework)Connection (algebraic framework)Geometry of quantum systems is mainlyphrased in algebraic terms of modules andalgebras. Connections on modules aregeneralization of a linear connection on a smooth vector bundle E\to...
External links
- G. SardanashvilyGennadi SardanashvilyGennadi Sardanashvily is a theoretical physicist, a principal research scientist of Moscow State University.- Biography :...
, Fibre bundles, jet manifolds and Lagrangian theory. Lectures for theoreticians,arXiv: 0908.1886

