
Supergeometry
Encyclopedia
Supergeometry is differential geometry of module
s over graded commutative algebra
s, supermanifold
s and graded manifold
s. Supergeometry is part and parcel of many classical and quantum field theories involving odd field
s, e.g., SUSY
field theory, BRST theory, or supergravity
.
Supergeometry is formulated in terms of -graded module
-graded module
s and sheaves
over -graded commutative algebras (supercommutative algebra
-graded commutative algebras (supercommutative algebra
s). In particular, superconnections are defined as Koszul connections on these modules and sheaves. However, supergeometry is not particular noncommutative geometry
because of a different definition of a graded derivation
.
Graded manifold
s and supermanifold
s also are phrased in terms of sheaves of graded commutative algebras. Graded manifold
s are characterized by sheaves on smooth manifolds
, while supermanifold
s are constructed by gluing of sheaves of supervector spaces. Note that there are different types of supermanifolds. These are smooth supermanifolds (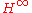 -,
-, 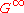 -,
-, 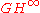 -supermanifolds),
-supermanifolds),  -supermanifolds, and DeWitt supermanifolds. In particular, supervector bundles and principal superbundles are considered in the category of
-supermanifolds, and DeWitt supermanifolds. In particular, supervector bundles and principal superbundles are considered in the category of  -supermanifolds. Note that definitions of principal superbundles and principal superconnections straightforwardly follow that of smooth principal bundle
-supermanifolds. Note that definitions of principal superbundles and principal superconnections straightforwardly follow that of smooth principal bundle
s and principal connection
s. Principal graded bundles also are considered in the category of graded manifold
s.
there is a different class of Quillen–Ne'eman
superbundles and superconnections. These superconnections have been applied to computing the Chern character
in K-theory
, noncommutative geometry
, and BRST formalism.
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over graded commutative algebra
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
s, supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
s and graded manifold
Graded manifold
Graded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
s. Supergeometry is part and parcel of many classical and quantum field theories involving odd field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
s, e.g., SUSY
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
field theory, BRST theory, or supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
.
Supergeometry is formulated in terms of
 -graded module
-graded moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s and sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
over
 -graded commutative algebras (supercommutative algebra
-graded commutative algebras (supercommutative algebraSupercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
s). In particular, superconnections are defined as Koszul connections on these modules and sheaves. However, supergeometry is not particular noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
because of a different definition of a graded derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
.
Graded manifold
Graded manifold
Graded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
s and supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
s also are phrased in terms of sheaves of graded commutative algebras. Graded manifold
Graded manifold
Graded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
s are characterized by sheaves on smooth manifolds
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, while supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
s are constructed by gluing of sheaves of supervector spaces. Note that there are different types of supermanifolds. These are smooth supermanifolds (
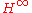 -,
-, 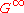 -,
-, 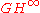 -supermanifolds),
-supermanifolds),  -supermanifolds, and DeWitt supermanifolds. In particular, supervector bundles and principal superbundles are considered in the category of
-supermanifolds, and DeWitt supermanifolds. In particular, supervector bundles and principal superbundles are considered in the category of  -supermanifolds. Note that definitions of principal superbundles and principal superconnections straightforwardly follow that of smooth principal bundle
-supermanifolds. Note that definitions of principal superbundles and principal superconnections straightforwardly follow that of smooth principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s and principal connection
Connection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
s. Principal graded bundles also are considered in the category of graded manifold
Graded manifold
Graded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
s.
there is a different class of Quillen–Ne'eman
Yuval Ne'eman
Yuval Ne'eman , was a renowned Israeli theoretical physicist, military scientist, and politician. He was a minister in the Israeli government in the 1980s and early 1990s.-Biography:...
superbundles and superconnections. These superconnections have been applied to computing the Chern character
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
in K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
, and BRST formalism.
See also
- SupermanifoldSupermanifoldIn physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
- Graded manifoldGraded manifoldGraded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
- SupersymmetrySupersymmetryIn particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
- Connection (algebraic framework)Connection (algebraic framework)Geometry of quantum systems is mainlyphrased in algebraic terms of modules andalgebras. Connections on modules aregeneralization of a linear connection on a smooth vector bundle E\to...
External links
- G. SardanashvilyGennadi SardanashvilyGennadi Sardanashvily is a theoretical physicist, a principal research scientist of Moscow State University.- Biography :...
, Lectures on supergeometry,arXiv: 0910.0092

