Euler's rotation theorem
Encyclopedia
In geometry
, Euler's rotation theorem states that, in three-dimensional space
, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two rotations is also a rotation. Therefore the set of rotations has a structure known as a rotation group
.
The theorem is named after Leonhard Euler
, who proved it in 1775 by an elementary geometric argument. The axis of rotation is known as an Euler pole. The extension of the theorem to kinematics
yields the concept of Instant axis of rotation.
In linear algebra terms, the theorem states that, in 3D space, any two Cartesian coordinate systems with a common origin are related by a rotation about some fixed axis. This also means that the product of two rotation matrices is again a rotation matrix and that for a non-identity rotation matrix it must happen that: one of its eigenvalues is 1 and the other two are -1, or it has only one real eigenvalue which is equal to unity. The eigenvector corresponding to this eigenvalue is the axis of rotation connecting the two systems.
or (in free translation):
To prove this, Euler considers a great circle on the sphere
and the great circle to which it is transported by the movement.
These two circles intersect in two (opposite) points
of which one, say A, is chosen.
This point lies on the initial circle and
thus is transported to a point a on the second circle.
On the other hand, A lies also on the translated circle,
and thus corresponds to a point α on the initial circle. Notice that the arc aA must be equal to the arc Aα.
Now Euler needs to construct point O in the surface of the sphere that is in the same position in reference to the arcs aA and αA. If such a point exists then:
Now Euler points out that the angles OAa and OaA must also be equal, since Oa and OA have the same length. Thus OAa and OAα are equal, proving O lies on the angle bisecting αAa. To provide a complete construction for O, we need only note that the arc aO may also be constructed such that AaO is the same as αAO. This completes the proof.
Euler provides a further construction that might be easier in practice. He proposes two planes:
Proposition. These two planes intersect in a diameter. This diameter is the one we are looking for.
Proof. Let's call O to any of the endpoints (there are two) of this diameter over the sphere surface. Since αA is mapped on Aa and the triangles have the same angles, it follows that the triangle OαA is transported onto the triangle OAa. Therefore the point O has to remain fixed under the movement.
Corollaries
This also shows that the rotation of the sphere can be seen
as two consecutive reflections about the two planes described above.
Points in a mirror plane are invariant under reflection,
and hence the points on their intersection (a line: the axis of rotation) are invariant under both the reflections,
and hence under the rotation.
Another simple way to find the rotation axis is by considering the plane on which the points α , A , a lie. The rotation axis is obviously orthogonal to this plane, and passes through the center C of the sphere.
Given that for a rigid body any movement that leaves an axis invariant is a rotation, this also proves that any arbitrary composition of rotations is equivalent to a single rotation around a new axis.
A rotation matrix has the fundamental property that its inverse is its transpose, that is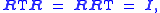
where I is the 3×3 identity matrix and superscript T indicates the transposed matrix.
Compute the determinant of this relation to find that a rotation matrix has determinant
±1. In particular,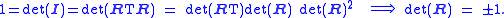
A rotation matrix with determinant +1 is a proper rotation, and one with a negative determinant −1 is an improper rotation, that is a reflection combined with a proper rotation.
It will now be shown that a rotation matrix R has at least one invariant vector n, i.e., R n = n. Because this requires that (R − I)n = 0, we see that the vector n must be an eigenvector of the matrix R with eigenvalue λ = 1. Thus, this is equivalent to showing that det(R − I) = 0.
Use the two relations: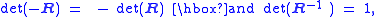
to compute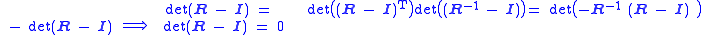
This shows that λ = 1 is a root (solution) of the secular equation, that is,
In other words, the matrix R − I is singular and has a non-zero kernel, that is, there is at least one non-zero vector, say n, for which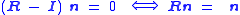
The line μn for real μ is invariant under R, i.e., μn is a rotation axis. This proves Euler's theorem.
is always equivalent (in this sense) to either the following matrix or to its vertical reflection:
Then, any orthogonal matrix is either a rotation or a reflection. It can be seen that any orthogonal matrix has only one real eigenvalue, which is +1 or −1. When it is +1 the matrix is a rotation. When −1, the matrix is a reflection.
If R has more than one invariant vector then φ = 0 and R = E. Any vector is an invariant vector of E.
An m×m matrix A has m orthogonal eigenvectors if and only if A is normal
, that is, if A†A = AA†. This result is equivalent to stating that
normal matrices can be brought to diagonal form by a unitary similarity transformation:
and U is unitary, that is,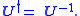
The eigenvalues α1, ..., αm are roots of the secular equation. If the matrix A happens to be unitary (and note that unitary matrices are normal), then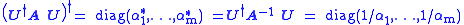
and it follows that the eigenvalues of a unitary matrix are on the unit circle in the complex plane: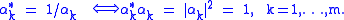
Also an orthogonal (real unitary) matrix has eigenvalues on the unit circle in the complex plane. Moreover, since its secular equation (an mth order polynomial in λ) has real coefficients, it follows that its roots appear in complex conjugate pairs, that is, if α is a root then so is α∗.
After recollection of these general facts from matrix theory, we return to the rotation matrix R. It follows from its realness and orthogonality that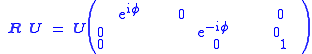
with the third column of the 3×3 matrix U equal to the invariant vector n.
Writing u1 and u2 for the first two columns of U, this equation gives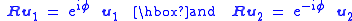
If u1 has eigenvalue 1, then φ= 0 and u2 has also eigenvalue 1, which implies that in that case R = E.
Finally, the matrix equation is transformed by means of a unitary matrix,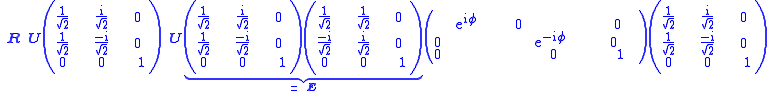
which gives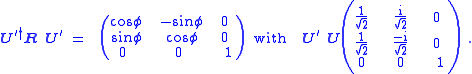
The columns of U′ are orthonormal. The third column is still n, the other two columns are perpendicular to n. This result implies that any orthogonal matrix R is equivalent to a rotation over an angle φ around an axis n.
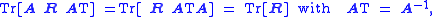
it follows that all matrices that are equivalent to R by an orthogonal matrix transformation have the same trace. The matrix transformation is clearly an equivalence relation
, that is, all equivalent matrices form an equivalence class. In fact, all proper rotation 3×3 rotation matrices form a group
, usually denoted by SO(3) (the special orthogonal group in 3 dimensions) and all matrices with the same trace form an equivalence class in this group.
Elements of such an equivalence class share their rotation angle, but all rotations are around different axes. If n is an eigenvector of R with eigenvalue 1, then An is an eigenvector of ARAT, also with eigenvalue 1. Unless A = E, n and An are different.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Euler's rotation theorem states that, in three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two rotations is also a rotation. Therefore the set of rotations has a structure known as a rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
.
The theorem is named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, who proved it in 1775 by an elementary geometric argument. The axis of rotation is known as an Euler pole. The extension of the theorem to kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
yields the concept of Instant axis of rotation.
In linear algebra terms, the theorem states that, in 3D space, any two Cartesian coordinate systems with a common origin are related by a rotation about some fixed axis. This also means that the product of two rotation matrices is again a rotation matrix and that for a non-identity rotation matrix it must happen that: one of its eigenvalues is 1 and the other two are -1, or it has only one real eigenvalue which is equal to unity. The eigenvector corresponding to this eigenvalue is the axis of rotation connecting the two systems.
Euler's theorem (1776)
Euler states the theorem as follows:
Theorema.
Quomodocunque sphaera circa centrum suum conuertatur, semper assignari potest diameter,
cuius directio in situ translato conueniat cum situ initiali.
or (in free translation):
- When a sphere is moved around its centre it is always possible to find a diameter whose direction in the displaced position is the same as in the initial position.
To prove this, Euler considers a great circle on the sphere
and the great circle to which it is transported by the movement.
These two circles intersect in two (opposite) points
of which one, say A, is chosen.
This point lies on the initial circle and
thus is transported to a point a on the second circle.
On the other hand, A lies also on the translated circle,
and thus corresponds to a point α on the initial circle. Notice that the arc aA must be equal to the arc Aα.
Now Euler needs to construct point O in the surface of the sphere that is in the same position in reference to the arcs aA and αA. If such a point exists then:
- it is necessary, that the distances OA and Oa are equal to each other; the arcs Oa and OA must be equal,
- it is necessary that the angles OaA and OAα are equal.
Now Euler points out that the angles OAa and OaA must also be equal, since Oa and OA have the same length. Thus OAa and OAα are equal, proving O lies on the angle bisecting αAa. To provide a complete construction for O, we need only note that the arc aO may also be constructed such that AaO is the same as αAO. This completes the proof.
Euler provides a further construction that might be easier in practice. He proposes two planes:
- the symmetry plane of the angle αAa (which passes through the centre C of the sphere), and
- the symmetry plane of the arc Aa (which also passes through C).
Proposition. These two planes intersect in a diameter. This diameter is the one we are looking for.
Proof. Let's call O to any of the endpoints (there are two) of this diameter over the sphere surface. Since αA is mapped on Aa and the triangles have the same angles, it follows that the triangle OαA is transported onto the triangle OAa. Therefore the point O has to remain fixed under the movement.
Corollaries
This also shows that the rotation of the sphere can be seen
as two consecutive reflections about the two planes described above.
Points in a mirror plane are invariant under reflection,
and hence the points on their intersection (a line: the axis of rotation) are invariant under both the reflections,
and hence under the rotation.
Another simple way to find the rotation axis is by considering the plane on which the points α , A , a lie. The rotation axis is obviously orthogonal to this plane, and passes through the center C of the sphere.
Given that for a rigid body any movement that leaves an axis invariant is a rotation, this also proves that any arbitrary composition of rotations is equivalent to a single rotation around a new axis.
Matrix proof
A spatial rotation is a linear map in one-to-one correspondence with a 3×3 rotation matrix R that transforms a coordinate vector x into X, that is Rx = X. Therefore, another version of Euler's theorem is that for every rotation R, there is a vector n for which Rn = n. The line μn is the rotation axis of R.A rotation matrix has the fundamental property that its inverse is its transpose, that is
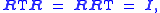
where I is the 3×3 identity matrix and superscript T indicates the transposed matrix.
Compute the determinant of this relation to find that a rotation matrix has determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
±1. In particular,
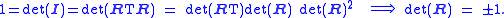
A rotation matrix with determinant +1 is a proper rotation, and one with a negative determinant −1 is an improper rotation, that is a reflection combined with a proper rotation.
It will now be shown that a rotation matrix R has at least one invariant vector n, i.e., R n = n. Because this requires that (R − I)n = 0, we see that the vector n must be an eigenvector of the matrix R with eigenvalue λ = 1. Thus, this is equivalent to showing that det(R − I) = 0.
Use the two relations:
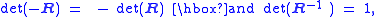
to compute
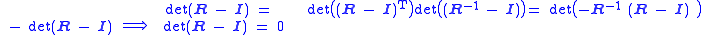
This shows that λ = 1 is a root (solution) of the secular equation, that is,
In other words, the matrix R − I is singular and has a non-zero kernel, that is, there is at least one non-zero vector, say n, for which
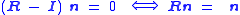
The line μn for real μ is invariant under R, i.e., μn is a rotation axis. This proves Euler's theorem.
Equivalence of an orthogonal matrix to a rotation matrix
Two matrices (representing linear maps) are said to be equivalent if there is change of basis that makes one equal to the other. A proper orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
is always equivalent (in this sense) to either the following matrix or to its vertical reflection:
Then, any orthogonal matrix is either a rotation or a reflection. It can be seen that any orthogonal matrix has only one real eigenvalue, which is +1 or −1. When it is +1 the matrix is a rotation. When −1, the matrix is a reflection.
If R has more than one invariant vector then φ = 0 and R = E. Any vector is an invariant vector of E.
Excursion into matrix theory
In order to prove the previous equation some facts from matrix theory must be recalled.An m×m matrix A has m orthogonal eigenvectors if and only if A is normal
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
, that is, if A†A = AA†. This result is equivalent to stating that
normal matrices can be brought to diagonal form by a unitary similarity transformation:
and U is unitary, that is,
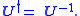
The eigenvalues α1, ..., αm are roots of the secular equation. If the matrix A happens to be unitary (and note that unitary matrices are normal), then
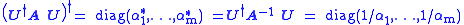
and it follows that the eigenvalues of a unitary matrix are on the unit circle in the complex plane:
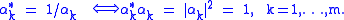
Also an orthogonal (real unitary) matrix has eigenvalues on the unit circle in the complex plane. Moreover, since its secular equation (an mth order polynomial in λ) has real coefficients, it follows that its roots appear in complex conjugate pairs, that is, if α is a root then so is α∗.
After recollection of these general facts from matrix theory, we return to the rotation matrix R. It follows from its realness and orthogonality that
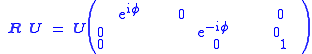
with the third column of the 3×3 matrix U equal to the invariant vector n.
Writing u1 and u2 for the first two columns of U, this equation gives
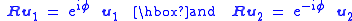
If u1 has eigenvalue 1, then φ= 0 and u2 has also eigenvalue 1, which implies that in that case R = E.
Finally, the matrix equation is transformed by means of a unitary matrix,
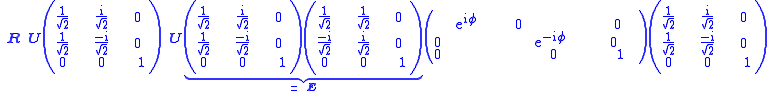
which gives
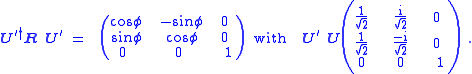
The columns of U′ are orthonormal. The third column is still n, the other two columns are perpendicular to n. This result implies that any orthogonal matrix R is equivalent to a rotation over an angle φ around an axis n.
Equivalence classes
It is of interest to remark that the trace (sum of diagonal elements) of the real rotation matrix given above is 1 + 2cosφ. Since a trace is invariant under an orthogonal matrix transformation: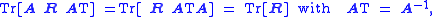it follows that all matrices that are equivalent to R by an orthogonal matrix transformation have the same trace. The matrix transformation is clearly an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, that is, all equivalent matrices form an equivalence class. In fact, all proper rotation 3×3 rotation matrices form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, usually denoted by SO(3) (the special orthogonal group in 3 dimensions) and all matrices with the same trace form an equivalence class in this group.
Elements of such an equivalence class share their rotation angle, but all rotations are around different axes. If n is an eigenvector of R with eigenvalue 1, then An is an eigenvector of ARAT, also with eigenvalue 1. Unless A = E, n and An are different.
Generators of rotations
Suppose we specify an axis of rotation by a unit vector [x, y, z] , and suppose we have an infinitely small rotation of angle Δθ about that vector. Expanding the rotation matrix as an infinite addition, and taking the first order approach, the rotation matrix ΔR is represented as:-
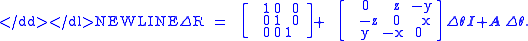
A finite rotation through angle θ about this axis may be seen as a succession of small rotations about the same axis. Approximating Δθ as θ/N where N is a large number, a rotation of θ about the axis may be represented as:
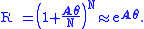
It can be seen that Euler's theorem essentially states that all rotations may be represented in this form. The product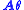
is the "generator" of the particular rotation, being the vector (x,y,z) associated with the matrix A. This shows that the rotation matrix and the axis-angle format are related by the exponential function.
Analysis is often easier in terms of these generators, rather than the full rotation matrix. Analysis in terms of the generators is known as the Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of the rotation group.
Quaternions
It follows from Euler's theorem that the relative orientation of any pair of coordinate systems may be specified by a set of three independent numbers. Sometimes a redundant fourth number is added to simplify operations with quaternion algebra. Three of these numbers are the direction cosines that orient the eigenvector. The fourth is the angle aboutAboutAbout may refer to:* About.com, an online source for original information and advice.* abOUT, an LGBT magazine* about: URI scheme, an internal URI scheme-People with the name:* Edmond François Valentin About, a French novelist...
the eigenvector that separates the two sets of coordinates. Such a set of four numbers is called a quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
.
While the quaternion as described above, does not involve complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, if quaternions are used to describe two successive rotations, they must be combined using the non-commutative quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
algebra derived by William Rowan HamiltonWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
through the use of imaginary numbers.
Rotation calculation via quaternions has come to replace the use of direction cosines in aerospace applications through their reduction of the required calculations, and their ability to minimize round-off errorRound-off errorA round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
s. Also, in computer graphicsComputer graphicsComputer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
the ability to perform spherical interpolation between quaternions with relative ease is of value.
Generalizations
In higher dimensions, any rigid motion that preserve a point in dimension 2n or 2n+1 is a composition of at most n rotations in orthogonal planes of rotationPlane of rotationIn geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
, though these planes need not be uniquely determined, and a rigid motion may fix multiple axes.
A rigid motion in 3 dimensions that does not necessarily fix a point is a "screw motion". This is because a composition of a rotation with a translation perpendicular to the axis is a rotation about a parallel axis, while composition with a translation parallel to the axis yields a screw motion; see screw axisScrew axisThe screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
. This gives rise to screw theoryScrew theoryScrew theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
.
See also
- Euler anglesEuler anglesThe Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
- Euler–Rodrigues parameters
- Rotation representationRotation representation (mathematics)In geometry a rotation representation expresses a rotation as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational kinematics is the science of describing with numbers the purely rotational motion of an object.According to Euler's rotation theorem...
- Rotation operator (vector space)Rotation operator (vector space)This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
- Angular velocityAngular velocityIn physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
- Rotation around a fixed axisRotation around a fixed axisRotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
External links
- Euler's original treatise in The Euler Archive: entry on E478, first publication 1976 (pdf)
- Euler's original text (in Latin) and English translation (by Johan Sten)
- Euler angles