
FKT algorithm
Encyclopedia
The FKT algorithm, named after Fisher
, Kasteleyn
, and Temperley
, counts the number of perfect matchings in a planar
graph in polynomial time. This same task is #P-complete for general graphs. Counting the number of matchings, even for planar graphs, is also #P-complete. The key idea is to convert the problem into a Pfaffian
computation of a skew-symmetric matrix derived from a planar embedding of the graph. The Pfaffian of this matrix is then computed efficiently using standard determinant algorithms.
and chemistry
, where the original question was: If diatomic molecules are adsorbed on a surface, forming a single layer, how many ways can they be arranged? The partition function
is an important quantity that encodes the statistical properties of a system at equilibrium and can be used to answer the previous question. However, trying to compute the partition function from its definition is not practical. Thus to exactly solve a physical system is to find an alternate form of the partition function for that particular physical system that is sufficiently simple to calculate exactly. In the early 1960s, the definition of exactly solvable was not rigorous. Computer science provided a rigorous definition with the introduction of polynomial time
, which dates to 1965. Similarly, the notation of not exactly solvable should correspond to #P-hardness, which was defined in 1979.
Another type of physical system to consider is composed of dimers, which is a polymer with two atoms. The dimer model counts the number of dimer coverings of a graph. Another physical system to consider is the bonding of H2O
molecules in the form of ice. This can be modelled as a directed, 3-regular
graph where the orientation of the edges at each vertex cannot all be the same. How many edge orientations does this model have?
Motivated by physical systems involving dimers, in 1961, Kasteleyn and Temperley-Fisher independently found the number of domino tilings for the m-by-n rectangle. This is equivalent to counting the number of perfect matchings for the m-by-n lattice graph
. By 1967, Kasteleyn had generalized this result to all planar graphs.
of the adjacency matrix
of a graph G corresponds to a perfect matching. Thus, if one can find an orientation of G to align all signs of the terms in Pfaffian
(no matter + or - ), then the absolute value of the Pfaffian
is just the number of perfect matchings in G. The FKT algorithm does such a task for a planar graph G.
Let G = (V, E) be an undirected graph with adjacency matrix
A. Define PM(n) to be the set of partitions of n elements into pairs, then the number of perfecting matchings in G is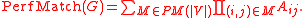
Closely related to this is the Pfaffian
for an n by n matrix A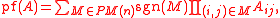
where sgn(M) is the sign of the permutation M. A Pfaffian orientation of G is a directed graph H with (1, −1, 0)-adjacency matrix B such that pf(B) = PerfMatch(G). In 1967, Kasteleyn proved that planar graphs have an efficiently computable Pfaffian orientation. Specifically, for a planar graph G, let H be a directed version of G were an odd number of edges are oriented clockwise for every face in a planar embedding of G. Then H is a Pfaffian orientation of G.
Finally, for any skew-symmetric matrix
A,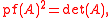
where det(A) is the determinant
of A. Since determinants are efficiently computable, so is PerfMatch(G).
for the adjacency matrix in the last step.
Kuratowski's theorem states that
Vijay Vazirani
generalized the FKT algorithm to graphs which do not contain a subgraph homeomorphic to K3,3. Since counting the number of perfect matchings in a general graph is #P-complete, some restriction on the input graph is required unless FP
, the function version of P
, is equal to #P
. Counting the number of matchings, which is known as the Hosoya index
, is also #P-complete even for planar graphs.
s on planar graphs via matchgates. For example, consider the planar version of the ice model mentioned above, which has the technical name #PL
-3-NAE-SAT
(where NAE stands for "not all equal"). Valiant found a polynomial time algorithm for this problem which uses matchgates.
Michael Fisher
Michael Ellis Fisher is an English physicist, as well as chemist and mathematician, known for his many seminal contributions...
, Kasteleyn
Pieter Kasteleyn
Pieter Willem Kasteleyn was a Dutch physicist famous for his contributions to the field of Statistical Mechanics.-Biography:...
, and Temperley
Harold Neville Vazeille Temperley
Harold Neville Vazeille Temperley is a mathematical physicist working on "lattice gases". His father, Harold William Vazeille Temperley, was a distinguished British historian....
, counts the number of perfect matchings in a planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
graph in polynomial time. This same task is #P-complete for general graphs. Counting the number of matchings, even for planar graphs, is also #P-complete. The key idea is to convert the problem into a Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
computation of a skew-symmetric matrix derived from a planar embedding of the graph. The Pfaffian of this matrix is then computed efficiently using standard determinant algorithms.
History
The problem of counting planar perfect matchings has its roots in statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, where the original question was: If diatomic molecules are adsorbed on a surface, forming a single layer, how many ways can they be arranged? The partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
is an important quantity that encodes the statistical properties of a system at equilibrium and can be used to answer the previous question. However, trying to compute the partition function from its definition is not practical. Thus to exactly solve a physical system is to find an alternate form of the partition function for that particular physical system that is sufficiently simple to calculate exactly. In the early 1960s, the definition of exactly solvable was not rigorous. Computer science provided a rigorous definition with the introduction of polynomial time
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, which dates to 1965. Similarly, the notation of not exactly solvable should correspond to #P-hardness, which was defined in 1979.
Another type of physical system to consider is composed of dimers, which is a polymer with two atoms. The dimer model counts the number of dimer coverings of a graph. Another physical system to consider is the bonding of H2O
H2O
H2O is the chemical formula for water and is also used as an abbreviation for the word "water". H2O or H2O It may also refer to:* H2O , a punk band**H2O , their self-titled debut album...
molecules in the form of ice. This can be modelled as a directed, 3-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
graph where the orientation of the edges at each vertex cannot all be the same. How many edge orientations does this model have?
Motivated by physical systems involving dimers, in 1961, Kasteleyn and Temperley-Fisher independently found the number of domino tilings for the m-by-n rectangle. This is equivalent to counting the number of perfect matchings for the m-by-n lattice graph
Lattice graph
The terms lattice graph, mesh graph, or grid graph refer to a number of categories of graphs whose drawing corresponds to some grid/mesh/lattice, i.e., its vertices correspond to the nodes of the mesh and its edges correspond to the ties between the nodes.-Square grid graph:A common type of a...
. By 1967, Kasteleyn had generalized this result to all planar graphs.
Explanation
The main insight is that every non-zero term in the PfaffianPfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
of the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of a graph G corresponds to a perfect matching. Thus, if one can find an orientation of G to align all signs of the terms in Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
(no matter + or - ), then the absolute value of the Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
is just the number of perfect matchings in G. The FKT algorithm does such a task for a planar graph G.
Let G = (V, E) be an undirected graph with adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
A. Define PM(n) to be the set of partitions of n elements into pairs, then the number of perfecting matchings in G is
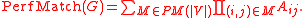
Closely related to this is the Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
for an n by n matrix A
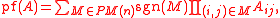
where sgn(M) is the sign of the permutation M. A Pfaffian orientation of G is a directed graph H with (1, −1, 0)-adjacency matrix B such that pf(B) = PerfMatch(G). In 1967, Kasteleyn proved that planar graphs have an efficiently computable Pfaffian orientation. Specifically, for a planar graph G, let H be a directed version of G were an odd number of edges are oriented clockwise for every face in a planar embedding of G. Then H is a Pfaffian orientation of G.
Finally, for any skew-symmetric matrix
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
A,
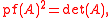
where det(A) is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A. Since determinants are efficiently computable, so is PerfMatch(G).
High-level description
- Compute a planar embeddingGraph embeddingIn topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
of G - Compute a spanning treeSpanning treeSpanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...
T1 of the input graph G - Give an arbitrary orientation to each edge in G that is also in T1
- Use the planar embedding to create an (undirected) graph T2 with the same vertex set as the dual graphDual graphIn mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
of G - Create an edge in T2 between two vertices if their corresponding faces in G share an edge in G that is not in T1
- For each leaf v in T2 (that is not also the root)
- Let e be the lone edge of G in the face corresponding to v that does not yet have an orientation
- Give e an orientation such that the number of edges oriented clock-wise is odd
- Remove v from T2
- Return the absolute value of the PfaffianPfaffianIn mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
of the (1, −1, 0)-adjacency matrix of G, which is the absolute value of the square root of the determinant
Generalizations
The sum of weighted perfect matchings can also be computed by using the Tutte matrixTutte matrix
In graph theory, the Tutte matrix A of a graph G = is a matrix used to determine the existence of a perfect matching: that is, a set of edges which is incident with each vertex exactly once....
for the adjacency matrix in the last step.
Kuratowski's theorem states that
- a finite graph is planar if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it contains no subgraph homeomorphicHomeomorphism (graph theory)In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...
to K5 (complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on five vertices) or K3,3 (complete bipartite graphComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
on two partitions of size three).
Vijay Vazirani
Vijay Vazirani
Vijay Virkumar Vazirani is an Indian American Professor of Computer Science at Georgia Tech.He received his Bachelor's degree from MIT in 1979 and his Ph.D. from the University of California, Berkeley in 1983. During the early to mid nineties, he was a Professor of Computer Science at the Indian...
generalized the FKT algorithm to graphs which do not contain a subgraph homeomorphic to K3,3. Since counting the number of perfect matchings in a general graph is #P-complete, some restriction on the input graph is required unless FP
FP (complexity)
In computational complexity theory, the complexity class FP is the set of function problems which can be solved by a deterministic Turing machine in polynomial time; it is the function problem version of the decision problem class P...
, the function version of P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, is equal to #P
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
. Counting the number of matchings, which is known as the Hosoya index
Hosoya index
The Hosoya index, also known as the Z index, of a graph is the total number of matchings in it. The Hosoya index is always at least one, because the empty set of edges is counted as a matching for this purpose. Equivalently, the Hosoya index is the number of non-empty matchings plus...
, is also #P-complete even for planar graphs.
Applications
The FKT algorithm has seen extensive use in holographic algorithmHolographic algorithm
In computer science, a holographic algorithm is an algorithm that uses a holographic reduction. A holographic reduction is a reduction that preserves the number of solutions. These concepts were introduced by Leslie Valiant and are a natural type of reduction for #P problems.Holographic algorithms...
s on planar graphs via matchgates. For example, consider the planar version of the ice model mentioned above, which has the technical name #PL
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
-3-NAE-SAT
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
(where NAE stands for "not all equal"). Valiant found a polynomial time algorithm for this problem which uses matchgates.
External links
- Presentation by Ashley Montanaro about the FKT algorithm
- More hisotry, information, and examples can be found in chapter 2 and section 5.3.2 of Dmitry Kamenetsky's PhD thesis

