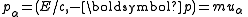Formulation of Maxwell's equations in special relativity
Encyclopedia
The covariant formulation of classical electromagnetism
refers to ways of writing the laws of classical electromagnetism (in particular, Maxwell's equations
and the Lorentz force
) in a form which is "manifestly covariant" (i.e. in terms of covariant four-vector
s and tensors), in the formalism of special relativity
. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another.
The Minkowski metric used in this article is assumed to have the form diag (+1, −1, −1, −1). The purely spatial components of the tensors (including vectors) are given in SI units. This article uses the classical treatment of tensors and the Einstein summation convention throughout. Where the equations are specified as holding in a vacuum, one could instead regard them as the formulation of Maxwell's equations in terms of total charge and current.
For a more general overview of the relationships between classical electromagnetism and special relativity, including various conceptual implications of this picture, see the article: Classical electromagnetism and special relativity
.
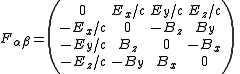
and the result of raising its indices is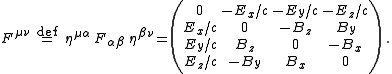
and electric charge density. In amperes/meter2, it is given by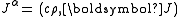
where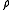
is the charge density, 
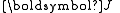is the current density, and 
is the speed of light
.
and magnetic vector potential, as follows: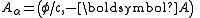
where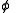
is the scalar potential
and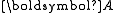
is the vector potential
.
The relation between the electromagnetic potentials and the electromagnetic fields is given by the following equation: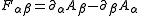
where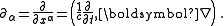
. In joules/meters3, it is given by
where
is the electric permittivity of vacuum
,
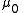is the magnetic permeability of vacuum, the Poynting vector
is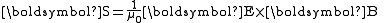
and the Maxwell stress tensor
is given by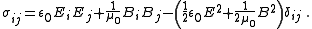
The electromagnetic stress-energy tensor is related to the electromagnetic field tensor by the equation: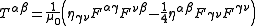
where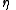
is the Minkowski metric tensor. Notice that we use the fact that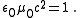
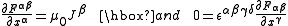
where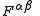
is the electromagnetic tensor
,
is the 4-current, 
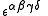is the Levi-Civita symbol
(a mathematical construct), and the indices behave according to the Einstein summation convention.
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss's Law
and Ampere's Law
(with Maxwell's correction). The second equation is an expression of the homogeneous equations, Faraday's law of induction
and Gauss's law for magnetism.
In the absence of sources, Maxwell's equations reduce to a wave equation
in the field strength:
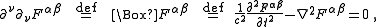
where,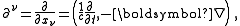
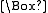is the d'Alembertian operator.
where all indices range from 0 to 3 (or, more descriptively,
ranges over the set {ct,x,y,z}), where 
is the speed of light in free space. The first tensor equation corresponds to four scalar equations, one for each value of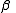 
. The second tensor equation actually corresponds to 
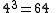different scalar equations, but only four of these are independent.
For convenience, professionals often write the 4-gradient
(that is, the derivative with respect to x) using abbreviated notations; for instance,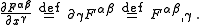
Using the latter notation, Maxwell's equations can be written as
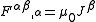
and
which expresses the fact that charge is conserved
is: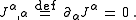
. Using the Lorentz force, Newton's law of motion can be written in relativistic form using the field strength tensor as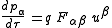
where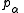
is the four-momentum
(see above),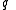
is the charge
,
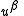is the four-velocity
(see above), and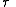
is the particle's proper time
.
In terms of (normal) time instead of proper time, the equation is
In a continuous medium, the 3D density of force combines with the density of power to form a covariant 4-vector,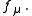
The spatial part is the result of dividing the force on a small cell (in 3-space) by the volume of that cell. The time component is 1/c times the power transferred to that cell divided by the volume of the cell. The density of Lorentz force
is the part of the density of force due to electromagnetism. Its spatial part is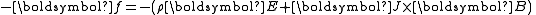
. In manifestly covariant notation it becomes:
Therefore,
The electromagnetic stress-energy tensor (defined above) satisfies the following differential equation, relating it to the electromagnetic tensor and the current four-vector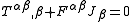
or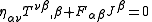
which expresses the conservation of linear momentum and energy by electromagnetic interactions.
is a Lorentz-invariant gauge condition. (This can be contrasted with other gauge conditions
such as the Coulomb gauge, which if it holds in one inertial frame will generally not hold in any other.) It is expressed in terms of the four-potential as follows:
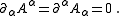
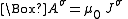
where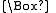
denotes the d'Alembertian.
Frequently, it is convenient to separate the current into two parts, the free current and the bound current, which are modeled by different equations.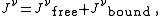
where
The bound current is derived from the magnetization
and electric polarization which form an antisymmetric contravariant magnetization-polarization tensor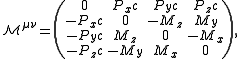
which determines the bound current
If this is combined with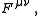
we get the antisymmetric contravariant electromagnetic displacement tensor which combines the electric displacement 
and the H-field 
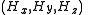as follows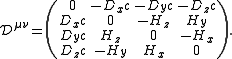
They are related by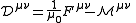
which is equivalent to the constitutive equations
and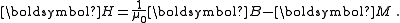 
And the result is that Ampère's law, 
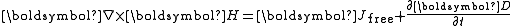, and Gauss's law
,
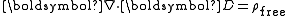, combine to form: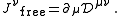
The bound current and free current as defined above are automatically and separately conserved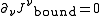
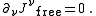
Thus we have reduced the problem of modeling the current,
to two (hopefully) easier problems — modeling the free current,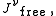 
and modeling the magnetization and polarization, 
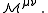For example, in the simplest materials at low frequencies, one has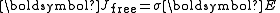
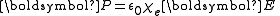
where one is in the instantaneously-comoving inertial frame of the material, σ is its electrical conductivity, χe is its electric susceptibility
, and χm is its magnetic susceptibility
.
(Lagrangian density) for classical electrodynamics (in joules/meter3) is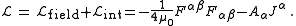
In the interaction term, the four-current should be understood as an abbreviation of many terms expressing the electric currents of other charged fields in terms of their variables; the four-current is not itself a fundamental field.
The Euler-Lagrange equation
for the electromagnetic Lagrangian density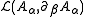
can be stated as follows: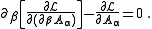
Noting
, The expression inside the square bracket is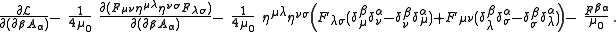
The second term is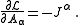
Therefore, the electromagnetic field's equations of motion are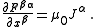
Separating the free currents from the bound currents, another way to write the Lagrangian density is as follows: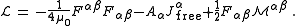
Using Euler-Lagrange equation, the equations of motion for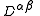
can be derived.
The equivalent expression in non-relativistic vector notation is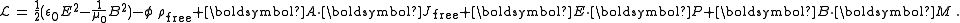
, the metric,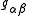
, is no longer a constant (
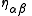) but can vary from place to place and time to time. In general relativity, the equations of electromagnetism in a vacuum become: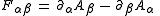
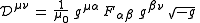
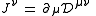
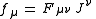
where
is the density of Lorentz force, 
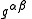is the reciprocal of the metric tensor 
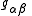, and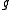 
is the determinant
of the metric tensor. Notice that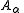
and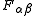 
are (ordinary) tensors while 
, 
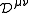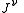, and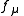 
are tensor densities
of weight +1. All derivatives are partial derivatives — if one replaced them with covariant derivative
s, the extra terms thereby introduced would cancel out.
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
refers to ways of writing the laws of classical electromagnetism (in particular, Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
) in a form which is "manifestly covariant" (i.e. in terms of covariant four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
s and tensors), in the formalism of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another.
The Minkowski metric used in this article is assumed to have the form diag (+1, −1, −1, −1). The purely spatial components of the tensors (including vectors) are given in SI units. This article uses the classical treatment of tensors and the Einstein summation convention throughout. Where the equations are specified as holding in a vacuum, one could instead regard them as the formulation of Maxwell's equations in terms of total charge and current.
For a more general overview of the relationships between classical electromagnetism and special relativity, including various conceptual implications of this picture, see the article: Classical electromagnetism and special relativity
Classical electromagnetism and special relativity
The theory of special relativity plays an important role in the modern theory of classical electromagnetism. First of all, it gives formulas for how electromagnetic objects, in particular the electric and magnetic fields, are altered under a Lorentz transformation from one inertial frame of...
.
Electromagnetic tensor
The electromagnetic tensor is the combination of the electric and magnetic fields into a covariant antisymmetric tensor. In volt·seconds/meter2, the field strength tensor is written in terms of fields as: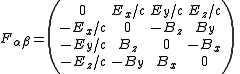and the result of raising its indices is
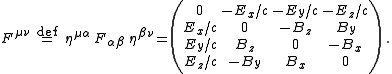
- where
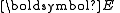is the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
,
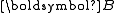the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, and
the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
- Caution: The signs in the tensor above depend on the convention used for the metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. The convention used here is +---, corresponding to the metric tensor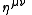
:
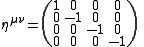
Four-Current
The four-current is the contravariant four-vector which combines electric currentElectric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
and electric charge density. In amperes/meter2, it is given by
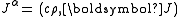
where
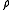is the charge density, 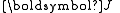is the current density, and is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
Four-potential
In volt·seconds/meter, the electromagnetic four-potential is a covariant four-vector containing the electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and magnetic vector potential, as follows:
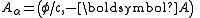
where
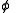is the scalar potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
and
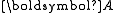is the vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
.
The relation between the electromagnetic potentials and the electromagnetic fields is given by the following equation:
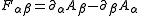
where
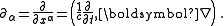
Electromagnetic stress-energy tensor
The electromagnetic stress-energy tensor is a contravariant symmetric tensor which is the contribution of the electromagnetic fields to the overall stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
. In joules/meters3, it is given by
where
is the electric permittivity of vacuumElectric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
,
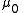is the magnetic permeability of vacuum, the Poynting vectorPoynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
is
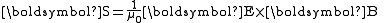
and the Maxwell stress tensor
Maxwell stress tensor
The Maxwell Stress Tensor is a mathematical object in physics, more precisely it is a second rank tensor used in classical electromagnetism to represent the interaction between electric/magnetic forces and mechanical momentum...
is given by
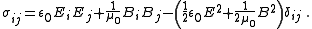
The electromagnetic stress-energy tensor is related to the electromagnetic field tensor by the equation:
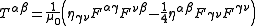
where
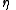is the Minkowski metric tensor. Notice that we use the fact that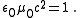Other, non-electromagnetic objects
For background purposes, we present here three other relevant four-vectors, which are not directly connected to electromagnetism, but which will be useful in this article:- In meters, the "position" or "coordinate" four-vector is
-
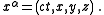
- In meters/second, the velocity four-vector (or four-velocityFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
) is
- In meters/second, the velocity four-vector (or four-velocity
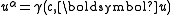
- where
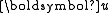is the (three-vector) velocity and 
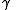is the Lorentz factorLorentz factorThe Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
associated with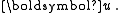
- In kilogram·meters/second, the four-momentumFour-momentumIn special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
(or momentum four-vector) of a particle is
- In kilogram·meters/second, the four-momentum
- where
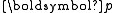is the (three-vector) momentum, 
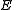is the energyKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
, and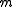
is the particle's rest mass.
Maxwell's equations in vacuo
In a vacuum (or for the microscopic equations, not including macroscopic material descriptions) Maxwell's equations can be written as two tensor equations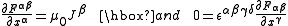where
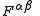is the electromagnetic tensorElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
,
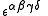is the 4-current, is the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
(a mathematical construct), and the indices behave according to the Einstein summation convention.
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss's Law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
and Ampere's Law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
(with Maxwell's correction). The second equation is an expression of the homogeneous equations, Faraday's law of induction
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
and Gauss's law for magnetism.
In the absence of sources, Maxwell's equations reduce to a wave equation
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
in the field strength:
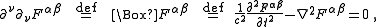
where,
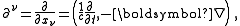
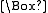is the d'Alembertian operator.Other notation
Without the summation convention or the Levi-Civita symbol, the equations would be writtenwhere all indices range from 0 to 3 (or, more descriptively,
ranges over the set {ct,x,y,z}), where is the speed of light in free space. The first tensor equation corresponds to four scalar equations, one for each value of 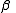. The second tensor equation actually corresponds to 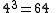different scalar equations, but only four of these are independent.For convenience, professionals often write the 4-gradient
Four-gradient
The four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...
(that is, the derivative with respect to x) using abbreviated notations; for instance,
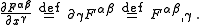
Using the latter notation, Maxwell's equations can be written as
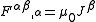
and
Continuity equation
The continuity equationContinuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
which expresses the fact that charge is conserved
Charge conservation
In physics, charge conservation is the principle that electric charge can neither be created nor destroyed. The net quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved...
is:
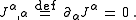
Lorentz force
Fields are detected by their effect on the motion of matter. Electromagnetic fields affect the motion of particles through the Lorentz forceLorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
. Using the Lorentz force, Newton's law of motion can be written in relativistic form using the field strength tensor as
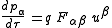
where
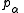is the four-momentumFour-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
(see above),
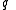is the chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
,
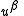is the four-velocityFour-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
(see above), and
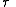is the particle's proper timeProper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
.
In terms of (normal) time instead of proper time, the equation is
In a continuous medium, the 3D density of force combines with the density of power to form a covariant 4-vector,
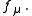The spatial part is the result of dividing the force on a small cell (in 3-space) by the volume of that cell. The time component is 1/c times the power transferred to that cell divided by the volume of the cell. The density of Lorentz forceLorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
is the part of the density of force due to electromagnetism. Its spatial part is
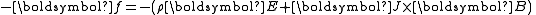. In manifestly covariant notation it becomes:Differential equation for electromagnetic stress-energy tensor
The relationship between Lorentz force and electromagnetic stress-energy tensor should be:Therefore,
The electromagnetic stress-energy tensor (defined above) satisfies the following differential equation, relating it to the electromagnetic tensor and the current four-vector
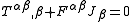
or
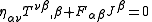
which expresses the conservation of linear momentum and energy by electromagnetic interactions.
Lorenz gauge condition
The Lorenz gauge conditionLorenz gauge condition
In electromagnetism, the Lorenz gauge or Lorenz gauge condition is a partial gauge fixing of the electromagnetic vector potential. The condition is that \partial_\mu A^\mu=0...
is a Lorentz-invariant gauge condition. (This can be contrasted with other gauge conditions
Gauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
such as the Coulomb gauge, which if it holds in one inertial frame will generally not hold in any other.) It is expressed in terms of the four-potential as follows:
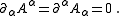
Maxwell's equations in the Lorenz gauge
In the Lorenz gauge, Maxwell's equations for a vacuum can be written as: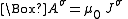where
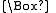denotes the d'Alembertian.Bound current
In order to solve the equations of electromagnetism given here, it is necessary to add information about how to calculate the electric current, Frequently, it is convenient to separate the current into two parts, the free current and the bound current, which are modeled by different equations.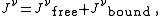where
The bound current is derived from the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
and electric polarization which form an antisymmetric contravariant magnetization-polarization tensor
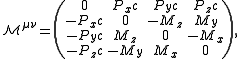
which determines the bound current
If this is combined with
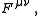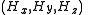we get the antisymmetric contravariant electromagnetic displacement tensor which combines the electric displacement and the H-field as follows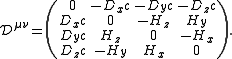They are related by
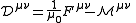
which is equivalent to the constitutive equations
and 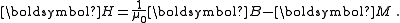And the result is that Ampère's law, 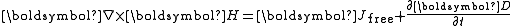, and Gauss's lawGauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
,
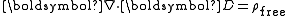, combine to form: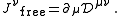The bound current and free current as defined above are automatically and separately conserved
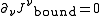
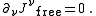
Thus we have reduced the problem of modeling the current,
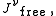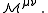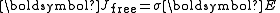
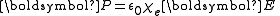
to two (hopefully) easier problems — modeling the free current, and modeling the magnetization and polarization, For example, in the simplest materials at low frequencies, one haswhere one is in the instantaneously-comoving inertial frame of the material, σ is its electrical conductivity, χe is its electric susceptibility
Electric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
, and χm is its magnetic susceptibility
Magnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
.
Lagrangian for classical electrodynamics
In a vacuum, the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
(Lagrangian density) for classical electrodynamics (in joules/meter3) is
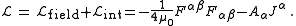
In the interaction term, the four-current should be understood as an abbreviation of many terms expressing the electric currents of other charged fields in terms of their variables; the four-current is not itself a fundamental field.
The Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
for the electromagnetic Lagrangian density
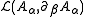can be stated as follows: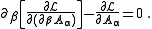Noting
, The expression inside the square bracket is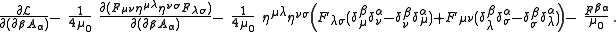The second term is
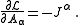
Therefore, the electromagnetic field's equations of motion are
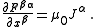
Separating the free currents from the bound currents, another way to write the Lagrangian density is as follows:
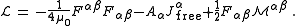
Using Euler-Lagrange equation, the equations of motion for
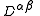can be derived.The equivalent expression in non-relativistic vector notation is
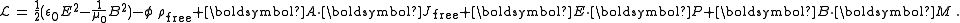
In general relativity
In general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the metric,
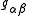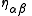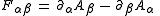
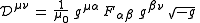
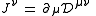
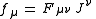
, is no longer a constant () but can vary from place to place and time to time. In general relativity, the equations of electromagnetism in a vacuum become:where
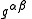is the density of Lorentz force, is the reciprocal of the metric tensor 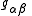, and 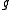is the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric tensor. Notice that
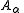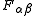and are (ordinary) tensors while 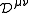, , 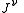and 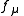are tensor densitiesTensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
of weight +1. All derivatives are partial derivatives — if one replaced them with covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s, the extra terms thereby introduced would cancel out.
See also
- Relativistic electromagnetismRelativistic electromagnetismRelativistic electromagnetism is a modern teaching strategy for developing electromagnetic field theory from Coulomb’s law and Lorentz transformations. Though Coulomb’s law expresses action at a distance, it is an easily understood electric force principle...
- Electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
- Liénard–Wiechert potential for a charge in arbitrary motion
- Nonhomogeneous electromagnetic wave equation
- Moving magnet and conductor problemMoving magnet and conductor problemThe moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in...
- Electromagnetic tensorElectromagnetic tensorThe electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
- Proca actionProca actionIn physics, in the area of field theory, the Proca action describes a massive spin-1 field of mass m in Minkowski spacetime. The field involved is a real vector field A...
- Stueckelberg action
- Quantum electrodynamicsQuantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
- Wheeler-Feynman absorber theory