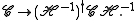Generalised circle
Encyclopedia
A generalized circle, also referred to as a "cline" or "circline", is a straight line or a circle
. The concept is mainly used in inversive geometry, because straight lines and circles have very similar properties in that geometry and are best treated together.
Inversive plane geometry is formulated on the plane extended by one point at infinity. A straight line is then thought of as a circle that passes through the point at infinity.
The fundamental transformations in inversive geometry, the inversions, have the property that they map generalized circles to generalized circles. Möbius transformations, which are compositions of inversions, inherit that property. These transformations do not necessarily map lines to lines and circles to circles: they can mix the two.
Inversions come in two kinds: inversions at circles and reflections at lines. Since the two have very similar properties, we combine them and talk about inversions at generalized circles.
Given any three distinct points in the extended plane, there exists precisely one generalized circle that passes through the three points.
The extended plane can be identified with the sphere
using a stereographic projection
. The point at infinity then becomes an ordinary point on the sphere, and all generalized circles become circles on the sphere.
A circle
Γ is the set of points
z in a plane that lie at radius
r from a center point γ.
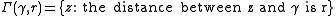
Using the complex plane
, we can treat γ as a complex number and circle Γ as a set of complex numbers.
Using the property that a complex number multiplied by its conjugate
gives us the square of the modulus of the number, and that its modulus is its Euclidean distance
from the origin, we can we can express the equation for Γ as follows:


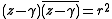
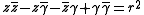
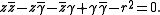
We can multiply this by a real constant
A to get an equation of the form
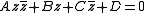
where A and D are real
, and B and C are complex conjugate
s. Note that when A is zero, this equation defines a straight line.
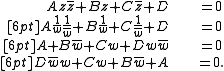
We see that straight lines through the origin (A = D = 0) are mapped to straight lines through the origin, straight lines not containing the origin (A = 0; D ≠ 0) to circles containing the origin, circles containing the origin (A ≠ 0; D = 0) to straight lines not containing the origin, and circles not containing the origin (A ≠ 0; D ≠ 0) to circles not containing the origin.
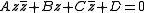
can be usefully put into the form of an invertible hermitian matrix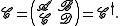
Two such invertible hermitian matrices specify the same generalized circle if and only if they differ by a real multiple.
To transform a generalized circle described by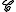 by the Möbius transformation
by the Möbius transformation 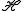 , you simply do
, you simply do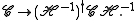
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. The concept is mainly used in inversive geometry, because straight lines and circles have very similar properties in that geometry and are best treated together.
Inversive plane geometry is formulated on the plane extended by one point at infinity. A straight line is then thought of as a circle that passes through the point at infinity.
The fundamental transformations in inversive geometry, the inversions, have the property that they map generalized circles to generalized circles. Möbius transformations, which are compositions of inversions, inherit that property. These transformations do not necessarily map lines to lines and circles to circles: they can mix the two.
Inversions come in two kinds: inversions at circles and reflections at lines. Since the two have very similar properties, we combine them and talk about inversions at generalized circles.
Given any three distinct points in the extended plane, there exists precisely one generalized circle that passes through the three points.
The extended plane can be identified with the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
using a stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. The point at infinity then becomes an ordinary point on the sphere, and all generalized circles become circles on the sphere.
Equation in the extended complex plane
The extended plane of inversive geometry can be identified with the extended complex plane, so that equations of complex numbers can be used to describe lines, circles and inversions.A circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
Γ is the set of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
z in a plane that lie at radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r from a center point γ.
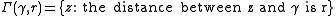
Using the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, we can treat γ as a complex number and circle Γ as a set of complex numbers.
Using the property that a complex number multiplied by its conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
gives us the square of the modulus of the number, and that its modulus is its Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
from the origin, we can we can express the equation for Γ as follows:


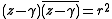
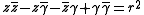
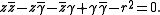
We can multiply this by a real constant
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
A to get an equation of the form
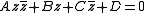
where A and D are real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, and B and C are complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
s. Note that when A is zero, this equation defines a straight line.
The transformation w = 1/z
It is now easy to see that the transformation w = 1/z maps generalized circles to generalized circles: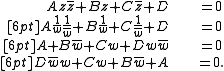
We see that straight lines through the origin (A = D = 0) are mapped to straight lines through the origin, straight lines not containing the origin (A = 0; D ≠ 0) to circles containing the origin, circles containing the origin (A ≠ 0; D = 0) to straight lines not containing the origin, and circles not containing the origin (A ≠ 0; D ≠ 0) to circles not containing the origin.
Representation by Hermitian matrices
The data defining the equation of a generalized circle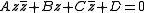
can be usefully put into the form of an invertible hermitian matrix
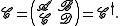
Two such invertible hermitian matrices specify the same generalized circle if and only if they differ by a real multiple.
To transform a generalized circle described by
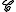 by the Möbius transformation
by the Möbius transformation 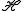 , you simply do
, you simply do