Georgi-Glashow model
Encyclopedia
In particle physics
, the Georgi–Glashow model is a particular grand unification theory
(GUT) proposed by Howard Georgi
and Sheldon Glashow in 1974. In this model the standard model
gauge groups SU(3)×SU(2)×U(1) are combined into a single simple
gauge group -- SU(5)
. The unified group SU(5) is then thought to be spontaneously broken
to the standard model subgroup at some high energy scale called the grand unification scale.
Since the Georgi–Glashow model combines lepton
s and quark
s into single irreducible representations, there exist interactions which do not conserve baryon
number, although they still conserve B-L
. This yields a mechanism for proton decay
, and the rate of proton decay can be predicted from the dynamics of the model. However, proton decay has not yet been observed experimentally, and the resulting lower limit on the lifetime of the proton contradicts the predictions of this model. However, the elegance of the model has led particle physicists to use it as the foundation for more complex models which yield longer proton lifetimes.
(For a more elementary introduction to how the representation theory of Lie algebras are related to particle physics, see the article Particle physics and representation theory
.)
This model suffers from the doublet-triplet splitting problem
.
, analogous to the Higgs field, and transforming in the adjoint
of SU(5) acquires a vacuum expectation value
proportional to the weak hypercharge
generator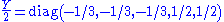
When this occurs SU(5) is spontaneously broken
to the subgroup
of SU(5) commuting with the group generated by Y. This unbroken subgroup is just the standard model
group: [SU(3)×SU(2)×U(1)_Y]/Z6.
Under the unbroken subgroup the adjoint 24 transforms as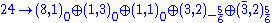
giving the gauge boson
s of the standard model. See restricted representation
.
The standard model quark
s and lepton
s fit neatly into representations of SU(5). Specifically, the left-handed fermion
s combine into 3 generations of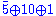
. Under the unbroken subgroup these transform as
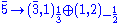(dc and l)
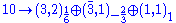(q, uc and ec)
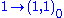(νc)
giving precisely the left-handed fermion
ic content of the standard model, where for every generation
dc, uc, ec and νc stand for anti-down-type quark, anti-up-type quark, anti-down-type lepton and anti-up-type lepton, respectively, and q and l stand for quark
and lepton
.
Note that fermions transforming as a 1 under SU(5) are now thought to be necessary because of the evidence for neutrino oscillation
s. Actually though, it is possible for there to be only left-handed neutrinos without any right-handed neutrinos if we could somehow introduce a tiny Majorana
coupling for the left-handed neutrinos.
Since the homotopy group
this model predicts 't Hooft-Polyakov monopole
s.
These monopoles have quantized Y magnetic charges. Since the electromagnetic charge Q is a linear combination of some SU(2) generator with Y/2, these monopoles also have quantized magnetic charges, where by magnetic here, we mean electromagnetic magnetic charges.
version of the model, we assign a Z2 matter parity to the chiral superfields with the matter fields having odd parity and the Higgs having even parity. This is unnecessary in the nonsupersymmetric version, but then, we can't protect the electroweak Higgs from quadratic radiative mass corrections. See hierarchy problem
. In the nonsupersymmetric version the action is invariant under a similar Z2 symmetry because the matter fields are all fermion
ic and thus must appear in the action in pairs, while the Higgs fields are boson
ic.
is a (complex)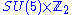
invariant cubic polynomial in the superfields. It is a linear combination of the following terms:
The first column is an Abbreviation of the second column (neglecting proper normalization factors), where capital indices are SU(5) indices, and i and j are the generation indices.
The last two rows presupposes the multiplicity of Nc is not zero (i.e. that a sterile neutrino
exists). The coupling Hu 10i 10j has coefficients which are symmetric in i and j. The coupling NciNcj has coefficients which are symmetric in i and j. Note that the number of sterile neutrino
generation
s need not be three, unless the SU(5) is embedded in a higher unification scheme such as SO(10)
.
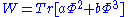
The F zeros corresponds to finding the stationary points of W subject to the traceless constraint
. So,
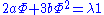
where λ is a Lagrange multiplier.
Up to an SU(5) (unitary) transformation,
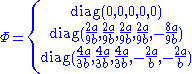
The three cases are called case I, II and III and they break the gauge symmetry into SU(5),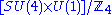
and 
respectively (the stabilizer of the VEV).
In other words, there at least three different superselection sections, which is typical for supersymmetric theories.
Only case III makes any phenomenological
sense and so, we will focus on this case from now onwards.
It can be verified that this solution together with zero VEVs for all the other chiral multiplets is a zero of the F-term
s and D-term
s. The matter parity remains unbroken (right up to the TeV scale).
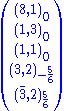. This 24 is a real representation, so the last two terms need explanation. Both 
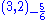and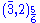 
are complex representations. However, the direct sum of both representation decomposes into two irreducible real representations and we only take half of the direct sum, i.e. one of the two real irreducible copies. The first three components are left unbroken. The adjoint Higgs also has a similar decomposition, except that it is complex. The Higgs mechanism
causes one real HALF of the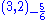
and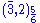 
of the adjoint Higgs to be absorbed. The other real half acquires a mass coming from the D-term
s. And the other three components of the adjoint Higgs,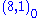
, 
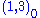and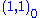 
acquire GUT scale masses coming from self pairings of the superpotential, aΦ2+b<Φ>Φ2.
The sterile neutrinos, if any exists, would also acquire a GUT scale Majorana mass coming from the superpotential coupling νc2.
Because of matter parity, the matter representations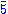
and 10 remain chiral.
It's the Higgs fields 5H and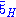
which are interesting.
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, the Georgi–Glashow model is a particular grand unification theory
Grand unification theory
The term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
(GUT) proposed by Howard Georgi
Howard Georgi
Howard Mason Georgi III, born January 6, 1947 in San Bernardino, California, is Harvard College Professor and Mallinckrodt Professor of Physics at Harvard University...
and Sheldon Glashow in 1974. In this model the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
gauge groups SU(3)×SU(2)×U(1) are combined into a single simple
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
gauge group -- SU(5)
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
. The unified group SU(5) is then thought to be spontaneously broken
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
to the standard model subgroup at some high energy scale called the grand unification scale.
Since the Georgi–Glashow model combines lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s and quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s into single irreducible representations, there exist interactions which do not conserve baryon
Baryon
A baryon is a composite particle made up of three quarks . Baryons and mesons belong to the hadron family, which are the quark-based particles...
number, although they still conserve B-L
B-L
In high energy physics, B − L is the difference between the baryon number and the lepton number .-Details:...
. This yields a mechanism for proton decay
Proton decay
In particle physics, proton decay is a hypothetical form of radioactive decay in which the proton decays into lighter subatomic particles, such as a neutral pion and a positron...
, and the rate of proton decay can be predicted from the dynamics of the model. However, proton decay has not yet been observed experimentally, and the resulting lower limit on the lifetime of the proton contradicts the predictions of this model. However, the elegance of the model has led particle physicists to use it as the foundation for more complex models which yield longer proton lifetimes.
(For a more elementary introduction to how the representation theory of Lie algebras are related to particle physics, see the article Particle physics and representation theory
Particle physics and representation theory
In physics, the connection between particle physics and representation theory is a natural connection, first noted by Eugene Wigner, between the properties of elementary particles and the representation theory of Lie groups and Lie algebras...
.)
This model suffers from the doublet-triplet splitting problem
Doublet-triplet splitting problem
In particle physics, the doublet-triplet problem is a problem of some Grand Unified Theories, such as SU, SO, E_6. Grand unified theories predict Higgs bosons arise from representations of the unified group that contain other states, in particular, states that are triplets of color...
.
Breaking SU(5)
SU(5) breaking occurs when a scalar fieldScalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
, analogous to the Higgs field, and transforming in the adjoint
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
of SU(5) acquires a vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
proportional to the weak hypercharge
Weak hypercharge
The weak hypercharge in particle physics is a conserved quantum number relating the electrical charge and the third component of weak isospin, and is similar to the Gell-Mann–Nishijima formula for the hypercharge of strong interactions...
generator
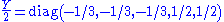
When this occurs SU(5) is spontaneously broken
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
to the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of SU(5) commuting with the group generated by Y. This unbroken subgroup is just the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
group: [SU(3)×SU(2)×U(1)_Y]/Z6.
Under the unbroken subgroup the adjoint 24 transforms as
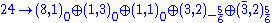
giving the gauge boson
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s of the standard model. See restricted representation
Restricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
.
The standard model quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s and lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s fit neatly into representations of SU(5). Specifically, the left-handed fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s combine into 3 generations of
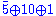. Under the unbroken subgroup these transform as 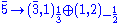(dc and l) 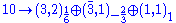(q, uc and e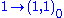c) (νc)giving precisely the left-handed fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic content of the standard model, where for every generation
Generation (particle physics)
In particle physics, a generation is a division of the elementary particles. Between generations, particles differ by their quantum number and mass, but their interactions are identical....
dc, uc, ec and νc stand for anti-down-type quark, anti-up-type quark, anti-down-type lepton and anti-up-type lepton, respectively, and q and l stand for quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
and lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
.
Note that fermions transforming as a 1 under SU(5) are now thought to be necessary because of the evidence for neutrino oscillation
Neutrino oscillation
Neutrino oscillation is a quantum mechanical phenomenon predicted by Bruno Pontecorvowhereby a neutrino created with a specific lepton flavor can later be measured to have a different flavor. The probability of measuring a particular flavor for a neutrino varies periodically as it propagates...
s. Actually though, it is possible for there to be only left-handed neutrinos without any right-handed neutrinos if we could somehow introduce a tiny Majorana
Majorana
Majorana may refer to:* Majorana equation, a relativistic wave equation* Majorana fermion, a concept in particle physics* Majorana spinor, a concept in quantum field theory* Origanum majorana, a somewhat cold-sensitive perennial herb...
coupling for the left-handed neutrinos.
Since the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
this model predicts 't Hooft-Polyakov monopole
't Hooft-Polyakov monopole
In theoretical physics, the t Hooft–Polyakov monopole is a topological soliton similar to the Dirac monopole but without any singularities. It arises in the case of a Yang–Mills theory with a gauge group G, coupled to a Higgs field which spontaneously breaks it down to a smaller group H via the...
s.
These monopoles have quantized Y magnetic charges. Since the electromagnetic charge Q is a linear combination of some SU(2) generator with Y/2, these monopoles also have quantized magnetic charges, where by magnetic here, we mean electromagnetic magnetic charges.
Matter parity
To prevent unwanted couplings in the supersymmetricSupersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
version of the model, we assign a Z2 matter parity to the chiral superfields with the matter fields having odd parity and the Higgs having even parity. This is unnecessary in the nonsupersymmetric version, but then, we can't protect the electroweak Higgs from quadratic radiative mass corrections. See hierarchy problem
Hierarchy problem
In theoretical physics, a hierarchy problem occurs when the fundamental parameters of some Lagrangian are vastly different than the parameters measured by experiment. This can happen because measured parameters are related to the fundamental parameters by a prescription known as renormalization...
. In the nonsupersymmetric version the action is invariant under a similar Z2 symmetry because the matter fields are all fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic and thus must appear in the action in pairs, while the Higgs fields are boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic.
Chiral superfields
As complex representations:| label | description | multiplicity | SU(5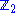) rep |  rep |
| Φ | GUT Higgs field | 1 | 24 |
| Hu | electroweak Higgs field | 1 | 5 |
| Hd | electroweak Higgs field | 1 |  |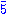
 |
matter fields | 3 |  |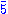
| 10 | matter fields | 3 | 10 |
| Nc | sterile neutrinos | ??? | 1 |
Superpotential
A generic invariant renormalizable superpotentialSuperpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
is a (complex)
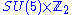invariant cubic polynomial in the superfields. It is a linear combination of the following terms:The first column is an Abbreviation of the second column (neglecting proper normalization factors), where capital indices are SU(5) indices, and i and j are the generation indices.
The last two rows presupposes the multiplicity of Nc is not zero (i.e. that a sterile neutrino
Sterile neutrino
Sterile neutrinosIn scientific literature, these particles are also variously referred to as right-handed neutrinos, inert neutrinos, heavy neutrinos, or neutral heavy leptons . are a hypothetical type of neutrino that do not interact via any of the fundamental interactions of the Standard Model...
exists). The coupling Hu 10i 10j has coefficients which are symmetric in i and j. The coupling NciNcj has coefficients which are symmetric in i and j. Note that the number of sterile neutrino
Sterile neutrino
Sterile neutrinosIn scientific literature, these particles are also variously referred to as right-handed neutrinos, inert neutrinos, heavy neutrinos, or neutral heavy leptons . are a hypothetical type of neutrino that do not interact via any of the fundamental interactions of the Standard Model...
generation
Generation (particle physics)
In particle physics, a generation is a division of the elementary particles. Between generations, particles differ by their quantum number and mass, but their interactions are identical....
s need not be three, unless the SU(5) is embedded in a higher unification scheme such as SO(10)
SO(10) (physics)
In particle physics, one of the grand unified theories is based on the SO Lie group....
.
Vacua
The vacua correspond to the mutual zeros of the F and D terms. Let's first look at the case where the VEVs of all the chiral fields are zero except for Φ.The Φ sector
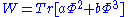
The F zeros corresponds to finding the stationary points of W subject to the traceless constraint
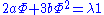
. So,where λ is a Lagrange multiplier.
Up to an SU(5) (unitary) transformation,
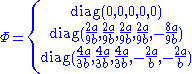
The three cases are called case I, II and III and they break the gauge symmetry into SU(5),
and respectively (the stabilizer of the VEV).In other words, there at least three different superselection sections, which is typical for supersymmetric theories.
Only case III makes any phenomenological
Phenomenology (science)
The term phenomenology in science is used to describe a body of knowledge that relates empirical observations of phenomena to each other, in a way that is consistent with fundamental theory, but is not directly derived from theory. For example, we find the following definition in the Concise...
sense and so, we will focus on this case from now onwards.
It can be verified that this solution together with zero VEVs for all the other chiral multiplets is a zero of the F-term
F-term
In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
s and D-term
D-term
In theoretical physics, one often analyzes theories with supersymmetry in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
s. The matter parity remains unbroken (right up to the TeV scale).
Decomposition
The gauge algebra 24 decomposes as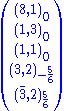. This 24 is a real representation, so the last two terms need explanation. Both 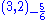and 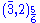are complex representations. However, the direct sum of both representation decomposes into two irreducible real representations and we only take half of the direct sum, i.e. one of the two real irreducible copies. The first three components are left unbroken. The adjoint Higgs also has a similar decomposition, except that it is complex. The Higgs mechanismHiggs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
causes one real HALF of the
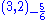and 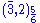of the adjoint Higgs to be absorbed. The other real half acquires a mass coming from the D-termD-term
In theoretical physics, one often analyzes theories with supersymmetry in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
s. And the other three components of the adjoint Higgs,
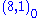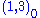, and 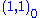acquire GUT scale masses coming from self pairings of the superpotential, aΦ2+b<Φ>Φ2.The sterile neutrinos, if any exists, would also acquire a GUT scale Majorana mass coming from the superpotential coupling νc2.
Because of matter parity, the matter representations
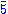and 10 remain chiral.It's the Higgs fields 5H and
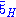which are interesting.
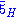
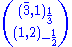
The two relevant superpotential terms here are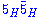
and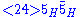 
. Unless there happens to be some fine tuningFine TuningFine Tuning was the name of XM Satellite Radio's eclectic music channel. The program director for Fine Tuning was Ben Smith and the tag line was, "The World's Most Interesting Music"....
, we would expect both the triplet terms and the doublet terms to pair up, leaving us with no light electroweak doublets. This is in complete disagreement with phenomenology. See doublet-triplet splitting problemDoublet-triplet splitting problemIn particle physics, the doublet-triplet problem is a problem of some Grand Unified Theories, such as SU, SO, E_6. Grand unified theories predict Higgs bosons arise from representations of the unified group that contain other states, in particular, states that are triplets of color...
for more details.