Gosset 2 22 honeycomb
Encyclopedia
In geometry
, an E6 honeycomb (or 222 honeycomb) is a tessellation of uniform polytopes in 6-dimensional Euclidean space.
 is a affine Coxeter group. 127 uniform honeycombs can be generated from this family by all ring permutations of its Coxeter-Dynkin diagram
is a affine Coxeter group. 127 uniform honeycombs can be generated from this family by all ring permutations of its Coxeter-Dynkin diagram
. There are no regular honeycombs in the family since its Coxeter diagram a nonlinear graph, but there are one simplest ones, with a single ring at the end of one of its 3 branches: 222.
The 222 honeycomb's vertex arrangement
is called the E6 lattice.
The 222 honeycomb is a uniform tessellation
. It can also be represented by the Schlafli symbol {3,3,32,2}. It is constructed from 221
facets and has a 122
vertex figure
, with 54 221 polytopes around every vertex.
upon a set of 7 hyperplane
mirrors in 6-dimensional space.
The facet information can be extracted from its Coxeter–Dynkin diagram, .
Removing a node on the end of one of the 2-node branches leaves the 221
, its only facet
type,
The vertex figure
is determined by removing the ringed node and ringing the neighboring node. This makes 122
, .
The edge figure is the vertex figure of the vertex figure, here being a birectified 5-simplex, t2{34}, .
The face figure is the vertex figure of the edge figure, here being a triangular duoprism
, {3}×{3}, .
in 6 dimensions, with kissing number 72.
 group is related to the
group is related to the 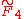 by a geometric folding, so this honeycomb can be projected into the 4-dimensional demitesseractic honeycomb.
by a geometric folding, so this honeycomb can be projected into the 4-dimensional demitesseractic honeycomb.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an E6 honeycomb (or 222 honeycomb) is a tessellation of uniform polytopes in 6-dimensional Euclidean space.
 is a affine Coxeter group. 127 uniform honeycombs can be generated from this family by all ring permutations of its Coxeter-Dynkin diagram
is a affine Coxeter group. 127 uniform honeycombs can be generated from this family by all ring permutations of its Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. There are no regular honeycombs in the family since its Coxeter diagram a nonlinear graph, but there are one simplest ones, with a single ring at the end of one of its 3 branches: 222.
The 222 honeycomb's vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
is called the E6 lattice.
222 honeycomb
| 222 honeycomb | |
|---|---|
| (no image) | |
| Type | Uniform tessellation |
| Coxeter symbol | 222 |
| Schläfli symbol | {3,3,32,2} |
| Coxeter–Dynkin diagram | |
| 6-face type | 221 Gosset 2 21 polytope In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure....  |
| 5-face types | 211 Pentacross In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells.... {34} |
| 4-face type | {33} Pentachoron In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid... |
| Cell type | {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
| Face type | {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
| Face figure | {3}×{3} duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
| Edge figure | t2{34} |
| Vertex figure | 122 Gosset 1 22 polytope In 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 ....  |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
 , [32,2,2] , [32,2,2] |
| Properties | vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... , facet-transitive |
The 222 honeycomb is a uniform tessellation
Uniform tessellation
In geometry, a uniform tessellation is a vertex-transitive tessellations made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex....
. It can also be represented by the Schlafli symbol {3,3,32,2}. It is constructed from 221
Gosset 2 21 polytope
In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure....
facets and has a 122
Gosset 1 22 polytope
In 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 ....
vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, with 54 221 polytopes around every vertex.
Construction
It is created by a Wythoff constructionWythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
upon a set of 7 hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
mirrors in 6-dimensional space.
The facet information can be extracted from its Coxeter–Dynkin diagram, .
Removing a node on the end of one of the 2-node branches leaves the 221
Gosset 2 21 polytope
In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure....
, its only facet
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
type,
The vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is determined by removing the ringed node and ringing the neighboring node. This makes 122
Gosset 1 22 polytope
In 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 ....
, .
The edge figure is the vertex figure of the vertex figure, here being a birectified 5-simplex, t2{34}, .
The face figure is the vertex figure of the edge figure, here being a triangular duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
, {3}×{3}, .
Kissing number
Each vertex of this tessellation is the center of a 5-sphere in the densest known packingSphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
in 6 dimensions, with kissing number 72.
Geometric folding
The group is related to the
group is related to the 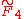 by a geometric folding, so this honeycomb can be projected into the 4-dimensional demitesseractic honeycomb.
by a geometric folding, so this honeycomb can be projected into the 4-dimensional demitesseractic honeycomb.
 |
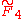 |
|---|---|
| {3,3,32,2} | {3,3,4,3} |

