
Grigorchuk group
Encyclopedia
In the mathematical
area of group theory
, the Grigorchuk group or the first Grigorchuk group is a finitely generated group constructed by Rostislav Grigorchuk
that provided the first example of a finitely generated group of intermediate (that is, faster than polynomial but slower than exponential) growth
. The group was originally constructed by Grigorchuk in a 1980 paper and he then proved in a 1984 paper that this group has intermediate growth, thus providing an answer to an important open problem posed by John Milnor
in 1968. The Grigorchuk group remains a key object of study in geometric group theory
, particularly in the study of the so-called branch groups and automata groups, and it has important connections with the theory of iterated monodromy group
s.
of a finitely generated group measures the asymptotics, as n → of the size of an n-ball in the Cayley graph
of the size of an n-ball in the Cayley graph
of the group (that is, the number of elements of G that can be expressed as words of length at most n in the generating set of G). The study of growth rates of finitely generated groups goes back to 1950s and is motivated in part by the notion of volume entropy
(that is, the growth rate of the volume of balls in the universal covering space of a compact
Riemannian manifold
in differential geometry. It is obvious that the growth rate of a finitely generated group is at most exponential
and it was also understood early on that finitely generated nilpotent group
s have polynomial growth. In 1968 John Milnor
posed a question about the existence of a finitely generated group of intermediate growth, that is, faster than any polynomial function and slower than any exponential function. An important result in the subject is Gromov's theorem on groups of polynomial growth
, obtained by Gromov in 1981, which shows that a finitely generated group has polynomial growth if and only if this group has a nilpotent
subgroup
of finite index
. Prior to Grigorchuk's work, there were many results establishing growth dichotomy (that is, that the growth is always either polynomial or exponential) for various classes of finitely generated groups, such as linear groups, solvable group
s, etc.
Grigorchuk's group G was constructed in a 1980 paper of Rostislav Grigorchuk
, where he proved that this group is infinite, periodic
and residually finite
. In a subsequent 1984 paper Grigorchuk proved that this group has intermediate growth (this result was announced by Grigorchuk in 1983). More precisely, he proved that G has growth b(n) that is faster than exp( ) but slower than exp(ns) where
) but slower than exp(ns) where 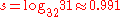 . Grigorchuk's group was also the first example of a group that is amenable
. Grigorchuk's group was also the first example of a group that is amenable
but not elementary amenable
, thus answering a problem posed by Mahlon Day in 1957.
Originally, Grigorchuk's group G was constructed as a group of Lebesgue-measure-preserving transformations on the unit interval, but subsequently simpler descriptions of G were found and it is now usually presented as a group of automorphisms of the infinite regular binary
rooted tree. The study of Grigorchuk's group informed in large part the development of the theory of branch groups, automata groups and self-similar groups in the 1990s–2000s and Grigorchuk's group remains a central object in this theory. Recently important connections between this theory and complex dynamics, particularly the notion of iterated monodromy group
s, have been uncovered in the work of Nekrashevych and others.
After Grigorchuk's 1984 paper, there were many subsequent results improving both upper and lower bounds on the growth of the Grigorchuk group, but the precise asymptotics of its growth is still unknown. It is conjectured that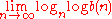 on the word growth exist, but even this remains a major open problem.
on the word growth exist, but even this remains a major open problem.
-preserving transformations of the unit interval, at present this group is usually given by its realization as a group of automorphisms of the infinite regular binary
rooted tree T2.
The tree T2 is realized as the set Σ* of all (including the empty string) finite strings in the alphabet Σ = {0,1}. The empty string Ø is the root vertex of T2 and for a vertex x of T2 the string x0 is the left child
of x and the string x1 is the right child
of x in T2. The group of all automorphisms Aut(T2) can thus be thought of as the group of all length-preserving permutations
σ of Σ* that also respect the initial segment relation, that is such that whenever a string x is an initial segment of a string y then σ(x) is an initial segment of σ(y).
The Grigorchuk group G is then defined as the subgroup
of Aut(T2) generated
by four specific elements a,b,c,d of Aut(T2), that is G = <a,b,c,d> ≤ Aut(T2), where the automorphisms a,b,c,d of T2 are defined recursively as follows:
Thus a swaps the right and left branch trees TL = 0Σ* and TR = 1Σ* below the root vertex Ø and the elements b,c,d can be represented as:
Here b = (a,c) means that b fixes the first level of T2 (that is, it fixes the strings 0 and 1) and that b acts on TL exactly as the automorphism a does on T2 and that b acts on TR exactly as the automorphism c does on T2. The notation c = (a,d) and d = (1,b) is interpreted similarly, where 1 in d = (1,b) means that d acts on TL as the identity map
does on T2.
Of the four elements a, b, c, d of Aut(T2) only the element a is defined explicitly and the elements b, c, d are defined inductively (by induction on the length |x| of a string x in Σ* ), that is, level by level.
The last property of G is sometimes called the contraction property. This property plays a key role in many proofs regarding G since it allows to use inductive arguments on the length of a word.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Grigorchuk group or the first Grigorchuk group is a finitely generated group constructed by Rostislav Grigorchuk
Rostislav Grigorchuk
Rostislav Ivanovich Grigorchuk is a Soviet and Ukrainian mathematician working in the area of group theory. He holds the rank of Distinguished Professor in the Mathematics Department of Texas A&M University...
that provided the first example of a finitely generated group of intermediate (that is, faster than polynomial but slower than exponential) growth
Growth rate (group theory)
In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
. The group was originally constructed by Grigorchuk in a 1980 paper and he then proved in a 1984 paper that this group has intermediate growth, thus providing an answer to an important open problem posed by John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
in 1968. The Grigorchuk group remains a key object of study in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, particularly in the study of the so-called branch groups and automata groups, and it has important connections with the theory of iterated monodromy group
Iterated monodromy group
In geometric group theory and dynamical systems the iterated monodromy group of a covering map is a group describing the monodromy action of the fundamental group on all iterations of the covering...
s.
History and generalizations
The growthGrowth rate (group theory)
In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
of a finitely generated group measures the asymptotics, as n →
 of the size of an n-ball in the Cayley graph
of the size of an n-ball in the Cayley graphCayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of the group (that is, the number of elements of G that can be expressed as words of length at most n in the generating set of G). The study of growth rates of finitely generated groups goes back to 1950s and is motivated in part by the notion of volume entropy
Volume entropy
The volume entropy is an asymptotic invariant of a compact Riemannian manifold that measures the exponential growth rate of the volume of metric balls in its universal cover. This concept is closely related with other notions of entropy found in dynamical systems and plays an important role in...
(that is, the growth rate of the volume of balls in the universal covering space of a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
in differential geometry. It is obvious that the growth rate of a finitely generated group is at most exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and it was also understood early on that finitely generated nilpotent group
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
s have polynomial growth. In 1968 John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
posed a question about the existence of a finitely generated group of intermediate growth, that is, faster than any polynomial function and slower than any exponential function. An important result in the subject is Gromov's theorem on groups of polynomial growth
Gromov's theorem on groups of polynomial growth
In geometric group theory, Gromov's theorem on groups of polynomial growth, named for Mikhail Gromov, characterizes finitely generated groups of polynomial growth, as those groups which have nilpotent subgroups of finite index....
, obtained by Gromov in 1981, which shows that a finitely generated group has polynomial growth if and only if this group has a nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of finite index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
. Prior to Grigorchuk's work, there were many results establishing growth dichotomy (that is, that the growth is always either polynomial or exponential) for various classes of finitely generated groups, such as linear groups, solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s, etc.
Grigorchuk's group G was constructed in a 1980 paper of Rostislav Grigorchuk
Rostislav Grigorchuk
Rostislav Ivanovich Grigorchuk is a Soviet and Ukrainian mathematician working in the area of group theory. He holds the rank of Distinguished Professor in the Mathematics Department of Texas A&M University...
, where he proved that this group is infinite, periodic
Periodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
and residually finite
Residually finite group
In the mathematical field of group theory, a group G is residually finite or finitely approximable if for every nontrivial element g in G there is a homomorphism h from G to a finite group, such thath \neq 1.\,...
. In a subsequent 1984 paper Grigorchuk proved that this group has intermediate growth (this result was announced by Grigorchuk in 1983). More precisely, he proved that G has growth b(n) that is faster than exp(
 ) but slower than exp(ns) where
) but slower than exp(ns) where 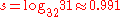 . Grigorchuk's group was also the first example of a group that is amenable
. Grigorchuk's group was also the first example of a group that is amenableAmenable group
In mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
but not elementary amenable
Elementary amenable group
In mathematics, a group is called elementary amenable if it can be built up from finite groups and abelian groups by a sequence of simple operations that result in amenable groups when applied to amenable groups...
, thus answering a problem posed by Mahlon Day in 1957.
Originally, Grigorchuk's group G was constructed as a group of Lebesgue-measure-preserving transformations on the unit interval, but subsequently simpler descriptions of G were found and it is now usually presented as a group of automorphisms of the infinite regular binary
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
rooted tree. The study of Grigorchuk's group informed in large part the development of the theory of branch groups, automata groups and self-similar groups in the 1990s–2000s and Grigorchuk's group remains a central object in this theory. Recently important connections between this theory and complex dynamics, particularly the notion of iterated monodromy group
Iterated monodromy group
In geometric group theory and dynamical systems the iterated monodromy group of a covering map is a group describing the monodromy action of the fundamental group on all iterations of the covering...
s, have been uncovered in the work of Nekrashevych and others.
After Grigorchuk's 1984 paper, there were many subsequent results improving both upper and lower bounds on the growth of the Grigorchuk group, but the precise asymptotics of its growth is still unknown. It is conjectured that
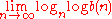 on the word growth exist, but even this remains a major open problem.
on the word growth exist, but even this remains a major open problem.Definition
Although initially the Grigorchuk group was defined as a group of Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
-preserving transformations of the unit interval, at present this group is usually given by its realization as a group of automorphisms of the infinite regular binary
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
rooted tree T2.
The tree T2 is realized as the set Σ* of all (including the empty string) finite strings in the alphabet Σ = {0,1}. The empty string Ø is the root vertex of T2 and for a vertex x of T2 the string x0 is the left child
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
of x and the string x1 is the right child
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
of x in T2. The group of all automorphisms Aut(T2) can thus be thought of as the group of all length-preserving permutations
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
σ of Σ* that also respect the initial segment relation, that is such that whenever a string x is an initial segment of a string y then σ(x) is an initial segment of σ(y).
The Grigorchuk group G is then defined as the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of Aut(T2) generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by four specific elements a,b,c,d of Aut(T2), that is G = <a,b,c,d> ≤ Aut(T2), where the automorphisms a,b,c,d of T2 are defined recursively as follows:
- a(0x) = 1x, a(1x) = 0x for every x in Σ*;
- b(0x) = 0a(x), b(1x) = 1c(x) for every x in Σ*;
- c(0x) = 0a(x), c(1x) = 1d(x) for every x in Σ*;
- d(0x) = 0x, d(1x) = 1b(x) for every x in Σ*.
Thus a swaps the right and left branch trees TL = 0Σ* and TR = 1Σ* below the root vertex Ø and the elements b,c,d can be represented as:
- b = (a,c),
- c = (a,d),
- d = (1,b).
Here b = (a,c) means that b fixes the first level of T2 (that is, it fixes the strings 0 and 1) and that b acts on TL exactly as the automorphism a does on T2 and that b acts on TR exactly as the automorphism c does on T2. The notation c = (a,d) and d = (1,b) is interpreted similarly, where 1 in d = (1,b) means that d acts on TL as the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
does on T2.
Of the four elements a, b, c, d of Aut(T2) only the element a is defined explicitly and the elements b, c, d are defined inductively (by induction on the length |x| of a string x in Σ* ), that is, level by level.
Basic features of the Grigorchuk group
The following are basic algebraic properties of the Grigorchuk group (see for proofs):- The group G is residually finiteResidually finite groupIn the mathematical field of group theory, a group G is residually finite or finitely approximable if for every nontrivial element g in G there is a homomorphism h from G to a finite group, such thath \neq 1.\,...
. Indeed, for every positive integer n let T[n] be the finite subtree of T2 which is the union of the first n levels of and let ρn:G→Aut(T[n]) be the restriction homomorphism that sends every element of G to its restriction to the finite tree T[n]. The groups Aut(T[n]) are finite and for every nontrivial g in G there exists n such that ρn(g) 1.
1. - Each of the elements a,b,c,d has orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
2 in G, that is, a2 = b2 = c2 = d2 = 1. Thus a = a−1, b = b−1, c = c−1 and d = d−1, so that every element of G can be written as a positive word in a,b,c,d, without using inverses. - The elements b,c,d pairwise commute and bc = cb = d, bd = db = c, dc = dc = b, so that <b,c,d>≤G is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of order 4 isomorphicGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of two cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of order 2. - The group G is generated by a and any two of the three elements b,c,d (e.g. G = <a, b, c>).
- Using the above recursive notation, in G we have aba = (c,a), aca = (d,a), ada = (b,1).
- The stabilizerGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
StG[1] in G of the 1st level of T2 is the subgroup generated by b, c, d, aba, aca, ada. The subgroup StG[1] is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 in G and
- G = StG[1]
 a StG[1].
a StG[1].
- Every element of G can be written as a (positive) word in a,b,c,d such that this word does not contain any subwords of the form aa, bb, cc, dd, cd, dc, bc, cb, bd, db. Such words are called reduced.
- A reduced word represents an element of StG[1] if and only if this word involves an even number of occurrences of a.
- If w is a reduced word of even length involving a positive even number of occurrences of a then there are some words u,v in a,b,c,d (not necessarily reduced) such that in G we have w = (u,v) and such that |u| ≤ |w|/2, |v| ≤ |w|/2. A similar statement holds if w is a reduced word of odd length involving a positive even number of occurrences of a where in the conclusion we have |u| ≤ (|w| + 1)/2, |v| ≤ (|w| + 1)/2.
The last property of G is sometimes called the contraction property. This property plays a key role in many proofs regarding G since it allows to use inductive arguments on the length of a word.
Properties and facts regarding the Grigorchuk group
- The group G is infinite.
- The group G is residually finite.
- The group G is a 2-groupP-groupIn mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
, that is, every element is G has finite orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
that is a power of 2. - The group G has intermediate growth.
- The group G is amenableAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
but not elementary amenableElementary amenable groupIn mathematics, a group is called elementary amenable if it can be built up from finite groups and abelian groups by a sequence of simple operations that result in amenable groups when applied to amenable groups...
. - The group G is just infinite, that is G is infinite but every proper quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of G is finite. - The group G has the congruence subgroup property: if H ≤ G then H has finite indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
in G if and only if there is a positive integer n such that the kernel Kern(ρn) of ρn is contained in H, that is Kern(ρn) ≤ H. - The group G has solvable word problemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
and solvable conjugacy problemConjugacy problemIn abstract algebra, the conjugacy problem for a group G with a given presentation is the decision problem of determining, given two words x and y in G, whether or not they represent conjugate elements of G...
(following from the contraction property mentioned in the previous section). - The group G has solvable subgroup membership problem, that is, there is an algorithm that, given arbitrary words w, u1,..., un in a, b, c, d, decides whether or not w represents an element of the subgroup generated by u1,..., un in G.
- The group G is subgroup separable, that is, every finitely generated subgroup is closed in the pro-finite topology on G.
- Every maximal subgroupMaximal subgroupIn mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
of G has finite indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
in G. - The group G is finitely generated but not finitely presentable.
See also
- Geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
- Growth of finitely generated groupsGrowth rate (group theory)In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
- Amenable groupAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
s - Iterated monodromy groupIterated monodromy groupIn geometric group theory and dynamical systems the iterated monodromy group of a covering map is a group describing the monodromy action of the fundamental group on all iterations of the covering...

