Helium atom - AbsoluteAstronomy.com

This article is about the physics of atomic helium. For other properties of helium, see helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...

.

Helium

Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...

is an element

Chemical element

A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...

and the next simplest atom

Atom

The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...

to solve after the hydrogen atom

Hydrogen atom

A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...

. Helium is composed of two electrons in orbit around a nucleus containing two protons along with either one or two neutrons, depending on the isotope

Isotopes of helium

Although there are eight known isotopes of helium , only helium-3 and helium-4 are stable. All radioisotopes are short-lived, the longest-lived being 6He with a half-life of 806.7 milliseconds. The least stable is the diproton, with a half-life of 3x10-27 seconds, even shorter than that of 5He...

. The hydrogen atom is used extensively to aid in solving the helium atom. The Niels Bohr model

Bohr model

In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...

of the atom gave a very accurate explanation of the hydrogen spectrum, but when it came to helium it collapsed. Werner Heisenberg

Werner Heisenberg

Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...

developed a modification of Bohr's analysis but it involved half-integral values for the quantum numbers. Thomas-Fermi theory, also known as density functional theory

Density functional theory

Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...

, is used to obtain the ground state energy levels of the helium atom along with the Hartree-Fock

Hartree-Fock

In computational physics and chemistry, the Hartree–Fock method is an approximate method for the determination of the ground-state wave function and ground-state energy of a quantum many-body system....

method.

Introduction

The Hamiltonian of helium, considered as a three-body system of two electrons and a nucleus and after separating out the centre-of-mass motion, can be written as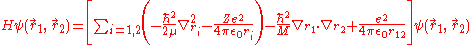

where

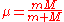is the reduced mass of an electron with respect to the nucleus,

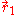and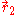

are the electron-nucleus distance vectors and

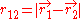. Consider

so that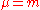

and the mass polarization term

disappear. The Hamiltonian in atomic units (a.u.) for simplicity is given by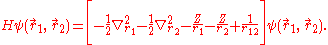

The presence of the electron-electron interaction term 1/r₁₂, makes this equation non separable. This means that

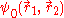can't be written as a single product of one-electron wave functions. This means that the wave function is entangled. Measurements cannot be made on on one particle without affecting the other. This is dealt with in the Hartree-Fock and Thomas-Fermi approximations.

Hartree-Fock Method

The Hartree-Fock method is used for a variety of atomic systems. However it is just an approximation, and there are more accurate and efficient methods used today to solve atomic systems. The "many-body problem

Many-body problem

The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...

" for helium and other few electron systems can be solved quite accurately. For example the ground state

Ground state

The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...

of helium is known to fifteen digits. In Hartree-Fock theory, the electrons are assumed to move in a potential created by the nucleus and the other electrons. The Hamiltonian

Hamiltonian

Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...

for helium with 2 electrons can be written as a sum of the Hamiltonians for each electron:

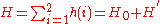
where the zero-order unperturbed Hamiltonian is

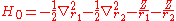
while the perturbation term:

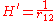
is the electron-electron interaction. H₀ is just the sum of the two hydrogenic Hamiltonians:

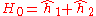
where

E_n₁, the energy eigenvalues and

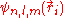, the corresponding eigenfunctions of the hydrogenic Hamiltonian will denote the normalized energy eigenvalues and the normalized eigenfunctions. So: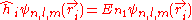

where

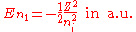
Neglecting the electron-electron repulsion term, the Schrödinger equation

Schrödinger equation

The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

for the spatial part of the two-electron wave function will reduce to the 'zero-order' equation

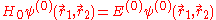
This equation is separable and the eigenfunctions can be written in the form of single products of hydrogenic wave functions:

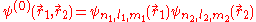
The corresponding energies are (in a.u.):

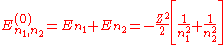
Note that the wave function

An exchange of electron labels corresponds to the same energy

. This particular case of degeneracy

Degeneracy

Degeneracy may refer to:* DegenerationIn science and mathematics:* Degeneracy , a property of quantum states sharing the same energy levels...

with respect to exchange of electron labels is called exchange degeneracy. The exact spatial wave functions of two-electron atoms must either be symmetric or antisymmetric

Antisymmetric

The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...

with respect to the interchange of the coordinates

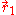and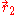

of the two electrons. The proper wave function then must be composed of the symmetric (+) and antisymmetric(-) linear combinations: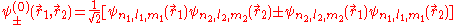

This comes from Slater determinants.

The factor

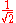normalizes

. In order to get this wave function into a single product of one-particle wave functions, we use the fact that this is in the ground state. So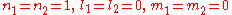

. So the

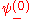will vanish, in agreement with the original formulation of the Pauli exclusion principle

Pauli exclusion principle

The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...

, in which two electrons cannot be in the same state. Therefor the wave function for helium can be written as

Where

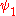and

use the wave functions for the hydrogen Hamiltonian. For helium, Z = 2 from

where E

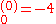a.u. which is approximately -108.8 eV, which corresponds to an ionization potential V

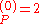a.u. (

eV). The experimental values are E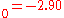

a.u. (

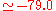eV) and V

a.u. (

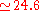eV).

The energy that we obtained is too low because the repulsion term between the electrons was ignored, whose affect is to raise the energy levels. As Z gets bigger, our approach should yield better results, since the electron-electron repulsion term will get smaller.

So far a very crude independent-particle approximation has been used, in which the electron-electron repulsion term is completely omitted. Splitting the Hamiltonian showed below will improve the results:

where

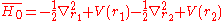
and

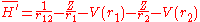
V(r) is a central potential which is chosen so that the effect of the perturbation

is small. The net effect of each electron on the motion of the other one is to screen somewhat the charge of the nucleus, so a simple guess for V(r) is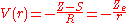

where S is a screening constant and the quantity Z_{_e} is the effective charge. The potential is a Coulomb interaction, so the corresponding individual electron energies are given (in a.u.) by

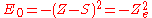
and the corresponding wave function is given by

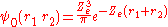
If Z_e was 1.70, that would make the expression above for the ground state energy agree with the experimental value E₀ = -2.903 a.u. of the ground state energy of helium. Since Z = 2 in this case, the screening constant is S = .30. For the ground state of helium, for the average shielding approximation, the screening effect of each electron on the other one is equivalent to about

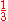of the electronic charge.

Thomas–Fermi method

Not long after Schrödinger developed the wave equation, the Thomas–Fermi model was developed. Density functional theory is used to describe the particle density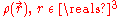

, and the ground state energy E(N), where N is the number of electrons in the atom. If there are a large number of electrons, the Schrödinger equation runs into problems, because it gets very very difficult to solve, even in the atoms ground states. This is where density functional theory comes in. Thomas-Fermi theory gives very good intuition of what is happening in the ground states of atoms and molecules with N electrons.

The energy functional for an atom with N electrons is given by:

Where

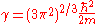
The electron density needs to be greater than or equal to 0,

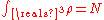, and

is convex.

In the energy functional, each term holds a certain meaning. The first term describes the minimum quantum-mechanical kinetic energy required to create the electron density

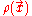for an N number of electrons. The next term is the attractive interaction of the electrons with the nuclei through the Coulomb potential

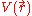. The final term is the electron-electron repulsion potential energy.

So the Hamiltonian for a system of many electrons can be written:

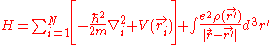
For helium, N = 2, so the Hamiltonian is given by:

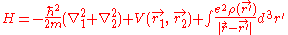
Where

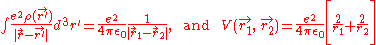
yielding

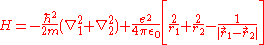
From the Hartree-Fock method, it is known that ignoring the electron-electron repulsion term, the energy is 8E₁ = -109 eV.

The variational method

To obtain a more accurate energy the variational principle

Variational principle

A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...

can be applied to the electron-electron potential V_ee using the wave function

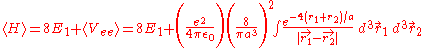
After integrating this, the result is:

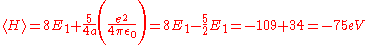
This is closer to the theoretical value, but if a better trial wave function is used, an even more accurate answer could be obtained. An ideal wave function would be one that doesn't ignore the influence of the other electron. In other words, each electron represents a cloud of negative charge which somewhat shields the nucleus so that the other electron actually sees an effective nuclear charge Z that is less than 2. A wave function of this type is given by:

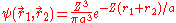
Treating Z as a variational parameter to minimize H. The Hamiltonian using the wave function above is given by:

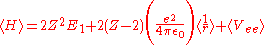
After calculating the expectation value of

and V_ee the expectation value of the Hamiltonian becomes:

The minimum value of Z needs to be calculated, so taking a derivative with respect to Z and setting the equation to 0 will give the minimum value of Z:

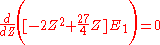
This shows that the other electron somewhat shields the nucleus reducing the effective charge from 2 to 1.69. So we obtain the most accurate result yet:

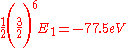
Where again, E₁ represents the ionization energy of hydrogen.

By using more complicated/accurate wave functions, the ground state energy of helium has been calculated closer and closer to the experimental value -78.95 eV. The variational approach has been refined to very high accuracy for a comprehensive regime of quantum states by G.W.F. Drake and co-workers as well as J.D. Morgan III, Jonathan Baker and Robert Hill using Hylleraas or Frankowski-Pekeris

Chaim L. Pekeris

Chaim Leib Pekeris was an Israeli-American physicist and mathematician. He made notable contributions to geophysics and the spectral theory of many-electron atoms, in particular the Helium atom. He was also one of the designers of the first computer in Israel, WEIZAC.-Biography:Pekeris was bon in...

basis functions. It should be noted that one needs to include relativistic

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

and quantum electrodynamic

Quantum electrodynamics

Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...

corrections to get full agreement with experiment to spectroscopic accuracy.

Introduction

Hartree-Fock Method

Thomas–Fermi method

The variational method

See also