Infinite monkey theorem - AbsoluteAstronomy.com

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

type a given text, such as the complete works of William Shakespeare

William Shakespeare

William Shakespeare was an English poet and playwright, widely regarded as the greatest writer in the English language and the world's pre-eminent dramatist. He is often called England's national poet and the "Bard of Avon"...

.

In this context, "almost surely" is a mathematical term with a precise meaning, and the "monkey" is not an actual monkey

Monkey

A monkey is a primate, either an Old World monkey or a New World monkey. There are about 260 known living species of monkey. Many are arboreal, although there are species that live primarily on the ground, such as baboons. Monkeys are generally considered to be intelligent. Unlike apes, monkeys...

, but a metaphor

Metaphor

A metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...

for an abstract device that produces a random sequence

Random sequence

The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let X1,...,Xn be independent random variables...". Yet as D. H. Lehmer stated in...

of letters and symbols ad infinitum

Ad infinitum

Ad infinitum is a Latin phrase meaning "to infinity."In context, it usually means "continue forever, without limit" and thus can be used to describe a non-terminating process, a non-terminating repeating process, or a set of instructions to be repeated "forever," among other uses...

. The probability

Probability

Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...

of a monkey exactly typing a complete work such as Shakespeare's Hamlet

Hamlet

The Tragical History of Hamlet, Prince of Denmark, or more simply Hamlet, is a tragedy by William Shakespeare, believed to have been written between 1599 and 1601...

is so tiny that the chance of it occurring during a period of time even a hundred thousand orders of magnitude longer than the age of the universe

Age of the universe

The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...

is extremely low, but not actually zero.

Variants of the theorem include multiple and even infinitely many typists, and the target text varies between an entire library and a single sentence. The history of these statements can be traced back to Aristotle

Aristotle

Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...

's On Generation and Corruption and Cicero

Cicero

Marcus Tullius Cicero , was a Roman philosopher, statesman, lawyer, political theorist, and Roman constitutionalist. He came from a wealthy municipal family of the equestrian order, and is widely considered one of Rome's greatest orators and prose stylists.He introduced the Romans to the chief...

's De natura deorum, through Blaise Pascal

Blaise Pascal

Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...

and Jonathan Swift

Jonathan Swift

Jonathan Swift was an Irish satirist, essayist, political pamphleteer , poet and cleric who became Dean of St...

, and finally to modern statements with their iconic typewriters. In the early 20th century, Émile Borel

Émile Borel

Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...

and Arthur Eddington used the theorem to illustrate the timescales implicit in the foundations of statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

Direct proof

There is a straightforward proof of this theorem. If two events are statistically independent, then the probability of both happening equals the product of the probabilities of each one happening independently. For example, if the chance of rain in Montreal

Montreal

Montreal is a city in Canada. It is the largest city in the province of Quebec, the second-largest city in Canada and the seventh largest in North America...

on a particular day is 0.3 and the chance of an earthquake

Earthquake

An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...

in San Francisco on that day is 0.008, then the chance of both happening on that same day is 0.3 × 0.008 = 0.0024.

Suppose the typewriter has 50 keys, and the word to be typed is banana. If we assume that the keys are pressed randomly (i.e., with equal probability) and independently, then the chance that the first letter typed is 'b' is 1/50, and the chance that the second letter typed is a is also 1/50, and so on, because events are independent. Therefore, the chance of the first six letters matching banana is × (1/50) × (1/50) × (1/50) × (1/50) × (1/50) = (1/50)⁶ = 1/15 625 000 000 ,
less than one in 15 billion.
For the same reason, the chance that the next 6 letters match banana is also (1/50)⁶, and so on.

From the above, the chance of not typing banana in a given block of 6 letters is 1 − (1/50)⁶. Because each block is typed independently, the chance X_n of not typing banana in any of the first n blocks of 6 letters is

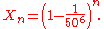
As n grows, X_n gets smaller. For an n of a million, X_n is roughly 0.9999, but for an n of 10 billion X_n is roughly 0.53 and for an n of 100 billion it is roughly 0.0017. As n approaches infinity, the probability X_n approaches

Limit of a function

In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....

zero; that is, by making n large enough, X_n can be made as small as is desired,This shows that the probability of typing "banana" in one of the predefined non-overlapping blocks of six letters tends to 1. In addition the word may appear across two blocks, so the estimate given is conservative. and the chance of typing banana approaches 100%.

The same argument shows why at least one of infinitely many monkeys will produce a text as quickly as it would be produced by a perfectly accurate human typist copying it from the original. In this case X_n = (1 − (1/50)⁶)ⁿ where X_n represents the probability that none of the first n monkeys types banana correctly on their first try. When we consider 100 billion monkeys, the probability falls to 0.17%, and as the number of monkeys n increases, the value of X_n – the probability of the monkeys failing to reproduce the given text – approaches zero arbitrarily closely. The limit, for n going to infinity, is zero.

However, for physically meaningful numbers of monkeys typing for physically meaningful lengths of time the results are reversed. If there are as many monkeys as there are particles in the observable universe

Observable universe

In Big Bang cosmology, the observable universe consists of the galaxies and other matter that we can in principle observe from Earth in the present day, because light from those objects has had time to reach us since the beginning of the cosmological expansion...

(10⁸⁰), and each types 1,000 keystrokes per second for 100 times the life of the universe (10²⁰ seconds), the probability of the monkeys replicating even a short book is nearly zero. See Probabilities, below.

Infinite strings

The two statements above can be stated more generally and compactly in terms of string

String (computer science)

In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....

s, which are sequences of characters chosen from some finite alphabet:

Given an infinite string where each character is chosen uniformly at random, any given finite string almost surely occurs as a substring at some position.
Given an infinite sequence of infinite strings, where each character of each string is chosen uniformly at random, any given finite string almost surely occurs as a prefix of one of these strings.

Both follow easily from the second Borel–Cantelli lemma. For the second theorem, let E_k be the event

Event (probability theory)

In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...

that the kth string begins with the given text. Because this has some fixed nonzero probability p of occurring, the E_k are independent, and the below sum diverges,

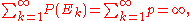
the probability that infinitely many of the E_k occur is 1. The first theorem is shown similarly; one can divide the random string into nonoverlapping blocks matching the size of the desired text, and make E_k the event where the kth block equals the desired string.The first theorem is proven by a similar if more indirect route in

Probabilities

Ignoring punctuation, spacing, and capitalization, a monkey typing letters uniformly at random has a chance of one in 26 of correctly typing the first letter of Hamlet

Hamlet

The Tragical History of Hamlet, Prince of Denmark, or more simply Hamlet, is a tragedy by William Shakespeare, believed to have been written between 1599 and 1601...

. It has a chance of one in 676 (26 × 26) of typing the first two letters. Because the probability shrinks exponential

Exponential growth

Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...

ly, at 20 letters it already has only a chance of one in 26²⁰ = 19,928,148,895,209,409,152,340,197,376 (almost 2 × 10²⁸). In the case of the entire text of Hamlet, the probabilities are so vanishingly small they can barely be conceived in human terms. The text of Hamlet contains approximately 130,000 letters.Using the Hamlet text from gutenberg, there are 132680 alphabetical letters and 199749 characters overall Thus there is a probability of one in 3.4 × 10^183,946 to get the text right at the first trial. The average number of letters that needs to be typed until the text appears is also 3.4 × 10^183,946For any required string of 130,000 letters from the set a-z, the average number of letters that needs to be typed until the string appears is (rounded) 3.4 × 10^183,946, except in the case that all letters of the required string are equal, in which case the value is about 4% more, 3.6 × 10^183,946. In that case failure to have the correct string starting from a particular position reduces with about 4% the probability of a correct string starting from the next position (i.e., for overlapping positions the events of having the correct string are not independent; in this case there is a positive correlation between the two successes, so the chance of success after a failure is smaller than the chance of success in general). The figure 3.4 × 10^183,946 is derived from n = 26¹³⁰⁰⁰⁰ by taking the logarithm of both sides: log₁₀(n) = 1300000×log₁₀(26) = 183946.5352, therefore n = 10^0.5352 × 10¹⁸³⁹⁴⁶ = 3.429 × 10¹⁸³⁹⁴⁶., or including punctuation, 4.4 × 10^360,783.26 letters ×2 for capitalisation, 12 for punctuation characters = 64, 199749×log₁₀(64) = 4.4 × 10^360,783.

Even if the observable universe were filled with monkeys the size of atoms typing from now until the heat death of the universe

Heat death of the universe

The heat death of the universe is a suggested ultimate fate of the universe, in which the universe has diminished to a state of no thermodynamic free energy and therefore can no longer sustain motion or life. Heat death does not imply any particular absolute temperature; it only requires that...

, their total probability to produce a single instance of Hamlet would still be a great many orders of magnitude less than one in 10^183,800. As Kittel

Charles Kittel

Charles Kittel is an American physicist. He was a Professor at University of California, Berkeley from 1951 and has been Professor Emeritus since 1978.- Life and work :...

and Kroemer

Herbert Kroemer

Herbert Kroemer , a professor of electrical and computer engineering at the University of California, Santa Barbara, received his Ph.D. in theoretical physics in 1952 from the University of Göttingen, Germany, with a dissertation on hot electron effects in the then-new transistor, setting the stage...

put it, "The probability of Hamlet is therefore zero in any operational sense of an event…", and the statement that the monkeys must eventually succeed "gives a misleading conclusion about very, very large numbers." This is from their textbook on thermodynamics

Thermodynamics

Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...

, the field whose statistical foundations motivated the first known expositions of typing monkeys.

Almost surely

The probability that an infinite randomly-generated string of text will contain a particular finite substring is 1, but this does not mean the substring's absence is "impossible", despite such an event having a probability of 0. For example, the immortal monkey could randomly type G as its first letter, G as its second, and G as every single letter thereafter, producing an infinite string of Gs; at no point must the monkey be "compelled" to type anything else.

There is a small but nonzero chance that a randomly generated string will consist of the same character repeated throughout; this chance approaches zero as the string's length approaches infinity. There is nothing special about such a monotonous sequence except that it is easy to describe; the same fact applies to any nameable specific sequence, such as "RGRGRG" repeated forever, or "a, b, aa, bb, aaa, bbb…".

If the hypothetical monkey has a typewriter with 90 equally-likely keys that include numerals and punctuation, then the first typed keys might be "3.14" (the first three digits of pi) with a probability of 1/90^4, which is 1/65,610,000. Equally probable is any other string of four characters allowed by the typewriter, such as "GGGG", "mATh", or "q%8e". The probability that 100 randomly typed keys will consist of the first 99 digits of pi, or any other particular sequence, is much lower: 1/90^100. If the monkey's allotted length of text is infinite, the chance of typing the entirety of the digits of pi is 0, which is just as possible as typing nothing but Gs (also probability 0).

The same applies to the event of typing a particular version of Hamlet followed by copies of itself ad infinitum; or Hamlet immediately followed by all the digits of pi; these specific strings are equally infinite, they are not prohibited by the terms of the thought problem, and they each have a prior probability of 0. In fact, any particular infinite sequence the immortal monkey types will have had a prior probability of 0, even though the monkey must type something.

This is an extension of the principle that a finite string of random text has a lower and lower probability of being a particular string the longer it is (though all specific strings are equally unlikely). This probability approaches 0 as the string approaches infinity. At the same time, the probability that the sequence contains a particular subsequence (such as the word MONKEY, or the 12th through 999th digits of pi, or a version of the King James Bible) increases as the total string increases. This probability approaches 1 as the total string approaches infinity, and thus the original theorem is correct.

Statistical mechanics

In one of the forms in which probabilists now know this theorem, with its "dactylographic" [i.e., typewriting] monkeys , appeared in Émile Borel

Émile Borel

's 1913 article "Mécanique Statistique et Irréversibilité" (Statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

and irreversibility), and in his book "Le Hasard" in 1914. His "monkeys" are not actual monkeys; rather, they are a metaphor for an imaginary way to produce a large, random sequence

Random sequence

of letters. Borel said that if a million monkeys typed ten hours a day, it was extremely unlikely that their output would exactly equal all the books of the richest libraries of the world; and yet, in comparison, it was even more unlikely that the laws of statistical mechanics would ever be violated, even briefly.

The physicist Arthur Eddington drew on Borel's image further in The Nature of the Physical World (1928), writing:
These images invite the reader to consider the incredible improbability of a large but finite number of monkeys working for a large but finite amount of time producing a significant work, and compare this with the even greater improbability of certain physical events. Any physical process that is even less likely than such monkeys' success is effectively impossible, and it may safely be said that such a process will never happen.

Origins and "The Total Library"

In a 1939 essay entitled "The Total Library", Argentine writer Jorge Luis Borges

Jorge Luis Borges

Jorge Francisco Isidoro Luis Borges Acevedo , known as Jorge Luis Borges , was an Argentine writer, essayist, poet and translator born in Buenos Aires. In 1914 his family moved to Switzerland where he attended school, receiving his baccalauréat from the Collège de Genève in 1918. The family...

traced the infinite-monkey concept back to Aristotle

Aristotle

's Metaphysics. Explaining the views of Leucippus

Leucippus

Leucippus or Leukippos was one of the earliest Greeks to develop the theory of atomism — the idea that everything is composed entirely of various imperishable, indivisible elements called atoms — which was elaborated in greater detail by his pupil and successor, Democritus...

, who held that the world arose through the random combination of atom

Atom

The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...

s, Aristotle notes that the atoms themselves are homogeneous and their possible arrangements only differ in shape, position and ordering. In On Generation and Corruption

On Generation and Corruption

On Generation and Corruption , , also known as On Coming to Be and Passing Away) is a treatise by Aristotle. Like many of his texts, it is both scientific and philosophic...

, the Greek philosopher compares this to the way that a tragedy and a comedy consist of the same "atoms", i.e., alphabetic characters. Three centuries later, Cicero

Cicero

's De natura deorum (On the Nature of the Gods) argued against the atomist worldview:
Borges follows the history of this argument through Blaise Pascal

Blaise Pascal

Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...

and Jonathan Swift

Jonathan Swift

Jonathan Swift was an Irish satirist, essayist, political pamphleteer , poet and cleric who became Dean of St...

, then observes that in his own time, the vocabulary had changed. By 1939, the idiom was "that a half-dozen monkeys provided with typewriters would, in a few eternities, produce all the books in the British Museum." (To which Borges adds, "Strictly speaking, one immortal monkey would suffice.") Borges then imagines the contents of the Total Library which this enterprise would produce if carried to its fullest extreme:
Borges's total library concept was the main theme of his widely read 1941 short story "The Library of Babel

The Library of Babel

"The Library of Babel" is a short story by Argentine author and librarian Jorge Luis Borges , conceiving of a universe in the form of a vast library containing all possible 410-page books of a certain format....

", which describes an unimaginably vast library consisting of interlocking hexagonal chambers, together containing every possible volume that could be composed from the letters of the alphabet and some punctuation characters.

Experiment

In 2003, scientists at Paignton Zoo

Paignton Zoo

Paignton Zoo Environmental Park, is a zoo in Paignton, Devon, England. The zoo is part of South West Environmental Parks Ltd which is owned by the Whitley Wildlife Conservation Trust . It is a combined zoo and botanic garden that welcomes over half a million visitors a year. WWCT also runs Living...

and the University of Plymouth

University of Plymouth

Plymouth University is the largest university in the South West of England, with over 30,000 students and is 9th largest in the United Kingdom by total number of students . It has almost 3,000 staff...

, in Devon

Devon

Devon is a large county in southwestern England. The county is sometimes referred to as Devonshire, although the term is rarely used inside the county itself as the county has never been officially "shired", it often indicates a traditional or historical context.The county shares borders with...

in England

England

England is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...

reported that they had left a computer keyboard in the enclosure of six Sulawesi Crested Macaque

Celebes Crested Macaque

The Celebes crested macaque , also known as the crested black macaque, Sulawesi crested macaque, or the black ape, is an Old World monkey that lives in the northeast of the Indonesian island of Sulawesi as well as on smaller neighboring islands.-Description:Its skin and hairless face is, with the...

s for a month; not only did the monkeys produce nothing but five pages consisting largely of the letter S

S is the nineteenth letter in the ISO basic Latin alphabet.-History: Semitic Šîn represented a voiceless postalveolar fricative . Greek did not have this sound, so the Greek sigma came to represent...

, (the full text may be found here:), they started by attacking the keyboard with a stone, and continued by urinating and defecating on it.

Evolution

In his 1931 book The Mysterious Universe, Eddington's rival James Jeans

James Hopwood Jeans

Sir James Hopwood Jeans OM FRS MA DSc ScD LLD was an English physicist, astronomer and mathematician.-Background:...

attributed the monkey parable to a "Huxley", presumably meaning Thomas Henry Huxley. This attribution is incorrect. Today, it is sometimes further reported that Huxley applied the example in a now-legendary debate

1860 Oxford evolution debate

The 1860 Oxford evolution debate took place at the Oxford University Museum on 30 June 1860, seven months after the publication of Charles Darwin's On the Origin of Species. Several prominent British scientists and philosophers participated, including Thomas Henry Huxley, Bishop Samuel...

over Charles Darwin

Charles Darwin

Charles Robert Darwin FRS was an English naturalist. He established that all species of life have descended over time from common ancestry, and proposed the scientific theory that this branching pattern of evolution resulted from a process that he called natural selection.He published his theory...

's On the Origin of Species with the Anglican Bishop of Oxford, Samuel Wilberforce

Samuel Wilberforce

Samuel Wilberforce was an English bishop in the Church of England, third son of William Wilberforce. Known as "Soapy Sam", Wilberforce was one of the greatest public speakers of his time and place...

, held at a meeting of the British Association for the Advancement of Science

British Association for the Advancement of Science

frame|right|"The BA" logoThe British Association for the Advancement of Science or the British Science Association, formerly known as the BA, is a learned society with the object of promoting science, directing general attention to scientific matters, and facilitating interaction between...

at Oxford on June 30, 1860. This story suffers not only from a lack of evidence, but the fact that in 1860 the typewriter itself had yet to emerge.

Despite the original mix-up, monkey-and-typewriter arguments are now common in arguments over evolution. For example, Doug Powell argues as a Christian apologist that even if a monkey accidentally types the letters of Hamlet, it has failed to produce Hamlet because it lacked the intention to communicate. His parallel implication is that natural laws could not produce the information content in DNA

DNA

Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...

. A more common argument is represented by Reverend John F. MacArthur

John F. MacArthur

John Fullerton MacArthur, Jr. is a United States evangelical writer and minister noted for his internationally known and broadcast radio program titled Grace to You...

, who claims that the genetic mutations necessary to produce a tapeworm from an amoeba are as unlikely as a monkey typing Hamlet's soliloquy, and hence the odds against the evolution of all life are impossible to overcome.

Evolutionary biologist Richard Dawkins

Richard Dawkins

Clinton Richard Dawkins, FRS, FRSL , known as Richard Dawkins, is a British ethologist, evolutionary biologist and author...

employs the typing monkey concept in his book The Blind Watchmaker

The Blind Watchmaker

The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe without Design is a 1986 book by Richard Dawkins in which he presents an explanation of, and argument for, the theory of evolution by means of natural selection. He also presents arguments to refute certain criticisms made on...

to demonstrate the ability of natural selection

Natural selection

Natural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....

to produce biological complexity

Complexity

In general usage, complexity tends to be used to characterize something with many parts in intricate arrangement. The study of these complex linkages is the main goal of complex systems theory. In science there are at this time a number of approaches to characterizing complexity, many of which are...

out of random mutation

Mutation

In molecular biology and genetics, mutations are changes in a genomic sequence: the DNA sequence of a cell's genome or the DNA or RNA sequence of a virus. They can be defined as sudden and spontaneous changes in the cell. Mutations are caused by radiation, viruses, transposons and mutagenic...

s. In a simulation experiment Dawkins has his weasel program

Weasel program

The weasel program, Dawkins' weasel, or the Dawkins weasel is a thought experiment and a variety of computer simulations illustrating it...

produce the Hamlet phrase METHINKS IT IS LIKE A WEASEL, starting from a randomly typed parent, by "breeding" subsequent generations and always choosing the closest match from progeny that are copies of the parent, with random mutations. The chance of the target phrase appearing in a single step is extremely small, yet Dawkins showed that it could be produced rapidly (in about 40 generations) using cumulative selection of phrases. The random choices furnish raw material, while cumulative selection imparts information. As Dawkins acknowledges, however, the weasel program is an imperfect analogy for evolution, as "offspring" phrases were selected "according to the criterion of resemblance to a distant ideal target." In contrast, Dawkins affirms, evolution has no long-term plans and does not progress toward some distant goal (such as humans). The weasel program is instead meant to illustrate the difference between nonrandom cumulative selection, and random single-step selection. In terms of the typing monkey analogy, this means that Romeo and Juliet could be produced relatively quickly if placed under the constraints of a nonrandom, Darwinian-type selection, by freezing in place any letters that happened to match the target text, and making that the template for the next generation of typing monkeys.

A different avenue for exploring the analogy between evolution and an unconstrained monkey lies in the problem that the monkey types only one letter at a time, independently of the other letters. Hugh Petrie argues that a more sophisticated setup is required, in his case not for biological evolution but the evolution of ideas:
James W. Valentine

James W. Valentine

James W. Valentine is an American evolutionary biologist and Professor Emeritus in the Department of Integrative Biology at the University of California, Berkeley...

, while admitting that the classic monkey's task is impossible, finds that there is a worthwhile analogy between written English and the metazoan genome in this other sense: both have "combinatorial, hierarchical structures" that greatly constrain the immense number of combinations at the alphabet level.

Literary theory

R. G. Collingwood

Robin George Collingwood was a British philosopher and historian. He was born at Cartmel, Grange-over-Sands in Lancashire, the son of the academic W. G. Collingwood, and was educated at Rugby School and at University College, Oxford, where he read Greats...

argued in 1938 that art cannot be produced by accident, and wrote as a sarcastic aside to his critics,
Nelson Goodman

Nelson Goodman

Henry Nelson Goodman was an American philosopher, known for his work on counterfactuals, mereology, the problem of induction, irrealism and aesthetics.-Career:...

took the contrary position, illustrating his point along with Catherine Elgin by the example of Borges' “Pierre Menard, Author of the Quixote”,
In another writing, Goodman elaborates, "That the monkey may be supposed to have produced his copy randomly makes no difference. It is the same text, and it is open to all the same interpretations…." Gérard Genette

Gérard Genette

Gérard Genette is a French literary theorist, associated in particular with the structuralist movement and such figures as Roland Barthes and Claude Lévi-Strauss, from whom he adapted the concept of bricolage.-Life:...

dismisses Goodman's argument as begging the question.

For Jorge J. E. Gracia

Jorge J. E. Gracia

Jorge J.E. Gracia is the Samuel P. Capen Chair, SUNY Distinguished Professor in the Department of Philosophy and Department of Comparative Literature in the State University of New York at Buffalo. Gracia was educated in Cuba, Canada and the United States and received his Ph.D...

, the question of the identity of texts leads to a different question, that of author. If a monkey is capable of typing Hamlet, despite having no intention of meaning and therefore disqualifying itself as an author, then it appears that texts do not require authors. Possible solutions include saying that whoever finds the text and identifies it as Hamlet is the author; or that Shakespeare is the author, the monkey his agent, and the finder merely a user of the text. These solutions have their own difficulties, in that the text appears to have a meaning separate from the other agents: what if the monkey operates before Shakespeare is born, or if Shakespeare is never born, or if no one ever finds the monkey's typescript?

Random document generation

The theorem concerns a thought experiment

Thought experiment

A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...

which cannot be fully carried out in practice, since it is predicted to require prohibitive amounts of time and resources. Nonetheless, it has inspired efforts in finite random text generation.

One computer program run by Dan Oliver of Scottsdale, Arizona, according to an article in The New Yorker

The New Yorker

The New Yorker is an American magazine of reportage, commentary, criticism, essays, fiction, satire, cartoons and poetry published by Condé Nast...

, came up with a result on August 4, 2004: After the group had worked for 42,162,500,000 billion billion monkey-years, one of the "monkeys" typed, “VALENTINE. Cease toIdor:eFLP0FRjWK78aXzVOwm)-‘;8.t" The first 19 letters of this sequence can be found in "The Two Gentlemen of Verona". Other teams have reproduced 18 characters from "Timon of Athens", 17 from "Troilus and Cressida", and 16 from "Richard II".

A website entitled The Monkey Shakespeare Simulator, launched on July 1, 2003, contained a Java applet

Java applet

A Java applet is an applet delivered to users in the form of Java bytecode. Java applets can run in a Web browser using a Java Virtual Machine , or in Sun's AppletViewer, a stand-alone tool for testing applets...

that simulates a large population of monkeys typing randomly, with the stated intention of seeing how long it takes the virtual monkeys to produce a complete Shakespearean play from beginning to end. For example, it produced this partial line from Henry IV, Part 2

Henry IV, Part 2

Henry IV, Part 2 is a history play by William Shakespeare, believed written between 1596 and 1599. It is the third part of a tetralogy, preceded by Richard II and Henry IV, Part 1 and succeeded by Henry V.-Sources:...

, reporting that it took "2,737,850 million billion billion billion monkey-years" to reach 24 matching characters:

RUMOUR. Open your ears; 9r"5j5&?OWTY Z0d...

Due to processing power limitations, the program uses a probabilistic model (by using a random number generator or RNG) instead of actually generating random text and comparing it to Shakespeare. When the simulator "detects a match" (that is, the RNG generates a certain value or a value within a certain range), the simulator simulates the match by generating matched text.

More sophisticated methods are used in practice for natural language generation

Natural language generation

Natural Language Generation is the natural language processing task of generating natural language from a machine representation system such as a knowledge base or a logical form...

. If instead of simply generating random characters one restricts the generator to a meaningful vocabulary and conservatively following grammar rules, like using a context-free grammar

Context-free grammar

In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....

, then a random document generated this way can even fool some humans (at least on a cursory reading) as shown in the experiments with SCIgen

SCIgen

SCIgen is a program created by scientists at the Massachusetts Institute of Technology that randomly generates nonsense in the form of computer science research papers, including graphs, diagrams, and citations...

, snarXiv

SnarXiv

snarXiv is a website spoofing the high-energy physics section of the popular electronic scientific paper repository arXiv. It was created in March 2010 by David Simmons-Duffin, a 3rd year Ph.D. student at Harvard University studying theoretical high-energy physics...

, and the Postmodernism Generator

Postmodernism Generator

The Postmodernism Generator is a computer program that automatically produces imitations of postmodernist writing, especially that of critical theory. It was written in 1996 by Andrew Bulhak of Monash University and is currently hosted at . The essays are produced from a formal grammar defined by a...

Testing of random number generators

Questions about the statistics describing how often an ideal monkey is expected

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

to type certain strings translate into practical tests for random number generators

Randomness tests

The issue of randomness is an important philosophical and theoretical question.Many random number generators in use today generate what are called "random sequences" but they are actually the result of prescribed algorithms and so they are called pseudo-random number generators.These generators do...

; these range from the simple to the "quite sophisticated". Computer science professors George Marsaglia

George Marsaglia

George Marsaglia was an American mathematician and computer scientist. He established the lattice structure of congruential random number generators in the paper "Random numbers fall mainly in the planes". This phenomenon is sometimes called the Marsaglia effect...

and Arif Zaman

Arif Zaman

Arif Zaman, Ph.D., is a Pakistani mathematician and an academic scientist. He is the Professor of Statistics and Mathematics and as well as Chairman of the Department of Mathematics at the School of Science and Engineering of the Lahore University of Management Sciences...

report that they used to call one such category of tests "overlapping m-tuple

Tuple

In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...

tests" in lecture, since they concern overlapping m-tuples of successive elements in a random sequence. But they found that calling them "monkey tests" helped to motivate the idea with students. They published a report on the class of tests and their results for various RNGs in 1993.

Popular culture

The infinite monkey theorem and its associated imagery is considered a popular and proverb

Proverb

A proverb is a simple and concrete saying popularly known and repeated, which expresses a truth, based on common sense or the practical experience of humanity. They are often metaphorical. A proverb that describes a basic rule of conduct may also be known as a maxim...

ial illustration of the mathematics of probability, widely known to the general public because of its transmission through popular culture rather than because of its transmission via the classroom.Examples of the theorem being referred to as proverbial include: Why Creativity Is Not like the Proverbial Typing Monkey. Jonathan W. Schooler, Sonya Dougal, Psychological Inquiry, Vol. 10, No. 4 (1999); and The Case of the Midwife Toad (Arthur Koestler

Arthur Koestler

Arthur Koestler CBE was a Hungarian author and journalist. Koestler was born in Budapest and, apart from his early school years, was educated in Austria...

, New York, 1972, page 30): "Neo-Darwinism does indeed carry the nineteenth-century brand of materialism to its extreme limits—to the proverbial monkey at the typewriter, hitting by pure chance on the proper keys to produce a Shakespeare sonnet." The latter is sourced from Parable of the Monkeys, a collection of historical references to the theorem in various formats.

This theorem was mentioned in part and used as a joke in the novel The Hitchhiker's Guide to the Galaxy

The Hitchhiker's Guide to the Galaxy

The Hitchhiker's Guide to the Galaxy is a science fiction comedy series created by Douglas Adams. Originally a radio comedy broadcast on BBC Radio 4 in 1978, it was later adapted to other formats, and over several years it gradually became an international multi-media phenomenon...

by Douglas Adams

Douglas Adams

Douglas Noel Adams was an English writer and dramatist. He is best known as the author of The Hitchhiker's Guide to the Galaxy, which started life in 1978 as a BBC radio comedy before developing into a "trilogy" of five books that sold over 15 million copies in his lifetime, a television...

: "Ford! There’s an infinite number of monkeys outside who want to talk to us about this script for Hamlet they’ve worked out" (chapter 9).

In the American cartoon The Simpsons

The Simpsons

The Simpsons is an American animated sitcom created by Matt Groening for the Fox Broadcasting Company. The series is a satirical parody of a middle class American lifestyle epitomized by its family of the same name, which consists of Homer, Marge, Bart, Lisa and Maggie...

episode "Last Exit to Springfield

Last Exit to Springfield

"Last Exit to Springfield" is the seventeenth episode of The Simpsons fourth season which originally aired March 11, 1993. It was directed by Mark Kirkland and was the last episode written by Jay Kogen and Wallace Wolodarsky...

", Mr Burns states: "This is a thousand monkeys working at a thousand typewriters. Soon they'll have written the greatest novel known to man. Let's see. (reading) 'It was the best of times, it was the "blurst" of times'?

A Tale of Two Cities

A Tale of Two Cities is a novel by Charles Dickens, set in London and Paris before and during the French Revolution. With well over 200 million copies sold, it ranks among the most famous works in the history of fictional literature....

You stupid monkey!"

The enduring, widespread popularity of the theorem was noted in the introduction to a 2001 paper, "Monkeys, Typewriters and Networks: The Internet in the Light of the Theory of Accidental Excellence" (Hoffmann and Hofmann). In 2002, an article in the Washington Post said: "Plenty of people have had fun with the famous notion that an infinite number of monkeys with an infinite number of typewriters and an infinite amount of time could eventually write the works of Shakespeare." In 2003, the previously mentioned Arts Council

Arts Council England

Arts Council England was formed in 1994 when the Arts Council of Great Britain was divided into three separate bodies for England, Scotland and Wales. It is a non-departmental public body of the Department of Culture, Media and Sport...

funded experiment involving real monkeys and a computer keyboard received widespread press coverage. In 2007, the theorem was listed by Wired

Wired (magazine)

Wired is a full-color monthly American magazine and on-line periodical, published since January 1993, that reports on how new and developing technology affects culture, the economy, and politics...

magazine in a list of eight classic thought experiment

Thought experiment

A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...

s.

A quotation attributed to a 1996 speech by Robert Wilensky states "We've heard that a million monkeys at a million keyboards could produce the complete works of Shakespeare; now, thanks to the Internet, we know that is not true."

External links

Ask Dr. Math article, August 1998, Adam Bridge
The Parable of the Monkeys, a bibliography with quotations
Planck Monkeys, on populating the cosmos with monkey particles
PixelMonkeys.org - Artist, Matt Kane's application of the Infinite Monkey Theorem on pixels to create images.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.