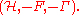K-homology
Encyclopedia
In mathematics
, K-homology is a homology
theory on the category
of compact
Hausdorff space
s. It classifies the elliptic pseudo-differential operator
s acting on the vector bundle
s over a space. In terms of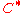 -algebras, it classifies the Fredholm module
-algebras, it classifies the Fredholm module
s over an algebra
.
An operator homotopy
between two Fredholm modules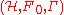 and
and 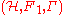 is a norm
is a norm
continuous
path
of Fredholm modules,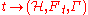 ,
,  Two Fredholm modules are then equivalent if they are related by unitary transformation
Two Fredholm modules are then equivalent if they are related by unitary transformation
s or operator homotopies. The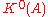 group
group
is the abelian group
of equivalence classes
of even Fredholm modules over A. The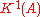 group is the abelian group of equivalence classes of odd Fredholm modules over A. Addition is given by direct summation
group is the abelian group of equivalence classes of odd Fredholm modules over A. Addition is given by direct summation
of Fredholm modules, and the inverse
of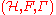 is
is 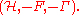
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, K-homology is a homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
theory on the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s. It classifies the elliptic pseudo-differential operator
Pseudo-differential operator
In mathematical analysis a pseudo-differential operator is an extension of the concept of differential operator. Pseudo-differential operators are used extensively in the theory of partial differential equations and quantum field theory....
s acting on the vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s over a space. In terms of
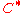 -algebras, it classifies the Fredholm module
-algebras, it classifies the Fredholm moduleFredholm module
In noncommutative geometry, a Fredholm module is a mathematical structure used to quantize the differential calculus. Such a module is, up to trivial changes, the same as the abstract elliptic operator introduced by .-Definition:...
s over an algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
An operator homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
between two Fredholm modules
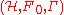 and
and 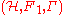 is a norm
is a normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
of Fredholm modules,
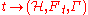 ,
,  Two Fredholm modules are then equivalent if they are related by unitary transformation
Two Fredholm modules are then equivalent if they are related by unitary transformationUnitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
s or operator homotopies. The
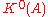 group
groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is the abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of equivalence classes
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
of even Fredholm modules over A. The
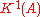 group is the abelian group of equivalence classes of odd Fredholm modules over A. Addition is given by direct summation
group is the abelian group of equivalence classes of odd Fredholm modules over A. Addition is given by direct summationDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of Fredholm modules, and the inverse
Inverse (mathematics)
In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below....
of
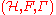 is
is