Kepler problem in general relativity
Encyclopedia
The two-body problem in general relativity is to determine the motion and gravitational field of two bodies interacting with one another by gravitation
, as described by the field equations of general relativity
. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet
orbiting its sun. Solutions are also used to describe the motion of binary star
s around each other, and estimate their gradual loss of energy through gravitational radiation. It is customary to assume that both bodies are point-like, so that tidal force
s and the specifics of their material composition can be neglected.
General relativity describes the gravitational field by curved space-time; the field equations governing this curvature are nonlinear and therefore difficult to solve in a closed form
. Only one exact solution, the Schwarzschild solution
, has been found for the Kepler problem; this solution pertains when the mass M of one body is overwhelmingly greater than the mass m of the other. If so, the larger mass may be taken as stationary and the sole contributor to the gravitational field. This is a good approximation for a photon passing a star and for a planet orbiting its sun. The motion of the lighter body (called the "particle" below) can then be determined from the Schwarzschild solution; the motion is a geodesic
("shortest path between two points") in the curved space-time. Such geodesic solutions account for the anomalous precession of the planet Mercury
, which is a key piece of evidence supporting the theory of general relativity. They also describe the bending of light in a gravitational field, another prediction famously used as evidence for general relativity.
If both masses are considered to contribute to the gravitational field, as in binary stars, the Kepler problem can be solved only approximately. The earliest approximation method to be developed was the post-Newtonian expansion
, an iterative method in which an initial solution is gradually corrected. More recently, it has become possible to solve Einstein's field equation using a computer instead of mathematical formulae. As the two bodies orbit each other, they will emit gravitational radiation
; this causes them to lose energy and angular momentum gradually, as illustrated by the binary pulsar PSR B1913+16.
, who worked as an assistant to the Danish astronomer Tycho Brahe
. Brahe took extraordinarily accurate measurements of the motion of the planets of the Solar System. From these measurements, Kepler was able to formulate Kepler's laws
, the first modern description of planetary motion:
Kepler published the first two laws in 1609 and the third law in 1619. They supplanted earlier models of the Solar System, such as those of Ptolemy
and Copernicus. Kepler's laws apply only in the limited case of the two-body problem. Voltaire
and Émilie du Châtelet
were the first to call them "Kepler's laws".
Nearly a century later, Isaac Newton
had formulated his three laws of motion
. In particular, Newton's second law states that a force F applied to a mass m produces an acceleration a given by the equation F=ma. Newton then posed the question: what must the force be that produces the elliptical orbits seen by Kepler? His answer came in his law of universal gravitation
, which states that the force between a mass M and another mass m is given by the formula
,
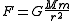where r is the distance between the masses and G is the gravitational constant
. Given this force law and his equations of motion, Newton was able to show that two point masses attracting each other would each follow perfectly elliptical orbits. The ratio of sizes of these ellipses is m/M, with the larger mass moving on a smaller ellipse. If M is much larger than m, then the larger mass will appear to be stationary at the focus of the elliptical orbit of the lighter mass m. This model can be applied approximately to the Solar System. Since the mass of the Sun is much larger than those of the planets, the force acting on each planet is principally due to the Sun; the gravity of the planets for each other can be neglected to first approximation.
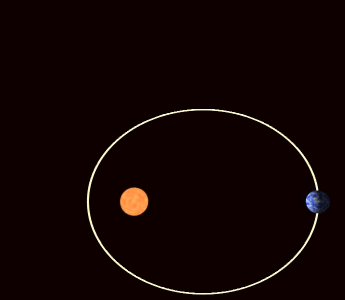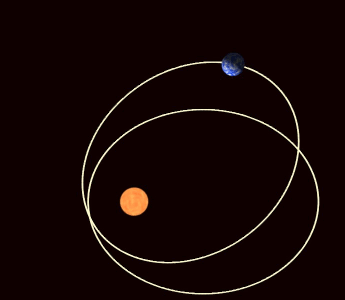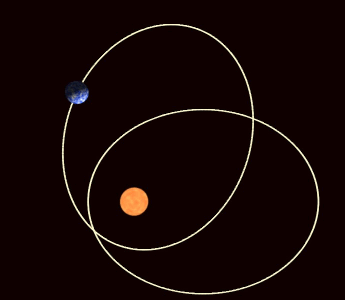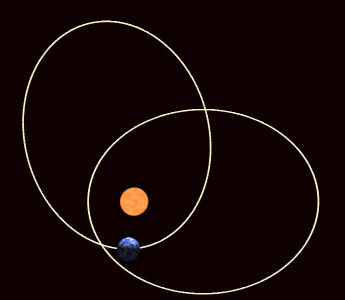If the potential energy between the two bodies is not exactly the 1/r potential of Newton's gravitational law but differs only slightly, then the ellipse of the orbit gradually rotates (among other possible effects). This apsidal precession
is observed for all the planets orbiting the Sun, primarily due to the oblateness of the Sun (it is not perfectly spherical) and the attractions of the other planets for one another. The apsides are the two points of closest and furthest distance of the orbit (the periapsis and apoapsis, respectively); apsidal precession corresponds to the rotation of the line joining the apsides. It also corresponds to the rotation of the Laplace–Runge–Lenz vector, which points along the line of apsides.
Newton's law of gravitation soon became accepted because it gave very accurate predictions of the apsidal precessions of all the planets. These calculations were carried out initially by Pierre-Simon Laplace
in the late 18th century, and refined by Félix Tisserand
in the later 19th century. Conversely, if Newton's law of gravitation had not predicted the apsidal precessions of the planets accurately, it would have to be discarded as a theory of gravitation. Such an anomalous precession was observed in the second half of the 19th century, and it led to the overthrow of Newtonian model of gravity and the development of general relativity
.
of the planet
Mercury
was not quite what it should be; the ellipse of its orbit was rotating (precessing) slightly faster than predicted by the traditional theory of Newtonian gravity, even after all the effects of the other planets had been accounted for. The effect is small (roughly 43 arcseconds of rotation per century), but well above the measurement error (roughly 0.1 arcseconds per century). Le Verrier realized the importance of his discovery immediately, and challenged astronomers and physicists alike to account for it. Several classical explanations were proposed, such as interplanetary dust, unobserved oblateness of the Sun
, an undetected moon of Mercury, or a new planet named Vulcan. After these explanations were discounted, some physicists were driven to the more radical hypothesis that Newton's
inverse-square law
of gravitation was incorrect. For example, some physicists proposed a power law
with an exponent that was slightly different from 2.
Others argued that Newton's law should be supplemented with a velocity-dependent potential. However, this implied a conflict with newtonian celestial dynamics. In his treatise on celestial mechanics, Laplace had shown that if the gravitational influence does not act instantaneously, then the motions of the planets themselves will not exactly conserve momentum (some of the momentum must then be ascribed to the mediator of the gravitational interaction, analogous to ascribing momentum to the mediator of the electromagnetic interaction.) As seen from a newtonian point of view, if gravitational influence does propagate at a finite speed, then at all points in time a planet is attracted to a point where the Sun was some time before, and not towards the instantaneous position of the Sun. On the assumption of the classical fundamentals, Laplace had shown that if gravity would propagate at a velocity in the order of the speed of light then the solar system would be unstable, and would not exist for a long time. The observation that the solar system is old allows one to put a lower limit on the speed of gravity
that is many orders of magnitude faster than the speed of light. Laplace's estimate for the velocity of gravity is not correct, because in a field theory which respects the principle of relativity, the attraction of a point charge which is moving at a constant velocity is towards the extrapolated instantaneous position, not to the apparent position it seems to occupy when looked atFeynman Lectures on Physics vol. II gives a thorough treatment of the analogous problem in electromagnetism. Feynman shows that for a moving charge, the non-radiative field is an attraction/repulsion not toward the apparent position of the particle, but toward the extrapolated position assuming that the particle continues in a straight line in a constant velocity. This is a notable property of the Liénard-Wiechert Potentials
which are used in the Wheeler-Feynman absorber theory. Presumably the same holds in linearized gravity.
To avoid those problems, between 1870 and 1900 many scientists used the electrodynamic laws of Wilhelm Eduard Weber
, Carl Friedrich Gauß, Bernhard Riemann
to produce stable orbits and to explain the Perihelion shift of Mercury's orbit. In 1890 Lévy succeeded in doing so by combining the laws of Weber and Riemann, whereby the speed of gravity
is equal to the speed of light
in his theory. And in another attempt Paul Gerber
(1898) even succeeded in deriving the correct formula for the Perihelion shift (which was identical to that formula later used by Einstein). However, because the basic laws of Weber and others were wrong (for example, Weber's law was superseded by Maxwell's theory), those hypotheses were rejected. Another attempt by Hendrik Lorentz
(1900), who already used Maxwell's theory, produced a Perihelion shift which was too low.
Around 1904–1905, the works of Hendrik Lorentz
, Henri Poincaré
and finally Albert Einstein
's special theory of relativity, exclude the possibility of propagation of any effects faster than the speed of light
. It followed that Newton's law of gravitation would have to be replaced with another law, compatible with the principle of relativity, while still obtaining the newtonian limit for circumstances where relativistic effects are negligible. Such attempts were made by Henri Poincaré
(1905), Hermann Minkowski
(1907) and Arnold Sommerfeld
(1910). In 1907 Einstein came to the conclusion that to achieve this a successor to special relativity was needed. From 1907 to 1915, Einstein worked towards a new theory, using his Equivalence Principle
as a key concept to guide his way. According to this principle, a uniform gravitational field acts equally on everything within it and, therefore, cannot be detected by a free-falling observer. Conversely, all local gravitational effects should be reproducible in a linearly accelerating reference frame, and vice versa. Thus, gravity acts like a fictitious force
such as the centrifugal force
or the Coriolis force, which result from being in an accelerated reference frame; all fictitious forces are proportional to the inertial mass, just as gravity is. To effect the reconciliation of gravity and special relativity
and to incorporate the equivalence principle
, something had to be sacrificed; that something was the long-held classical assumption that our space obeys the laws of Euclidean geometry
, e.g., that the Pythagorean theorem
is true experimentally. Einstein used a more general geometry, pseudo-Riemannian geometry
, to allow for the curvature of space
and time
that was necessary for the reconciliation; after eight years of work (1907–1915), he succeeded in discovering the precise way in which space-time should be curved in order to reproduce the physical laws observed in Nature, particularly gravitation. Gravity is distinct from the fictitious forces centrifugal force and coriolis force in the sense that the curvature of spacetime is regarded as physically real, whereas the fictitious forces are not regarded as forces. The very first solutions of his field equations
explained the anomalous precession of Mercury and predicted an unusual bending of light, which was confirmed after his theory was published. These solutions are explained below.
, triangles obey the Pythagorean theorem
, which states that the square distance ds2 between two points in space is the sum of the squares of its perpendicular components
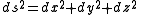
where dx, dy and dz represent the infinitesimal differences between the two points along the x, y and z axes of a Cartesian coordinate system
(add Figure here). Now imagine a world in which this is not quite true; a world where the distance is instead given by
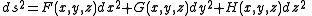
where F, G and H are arbitrary functions of position. It is not hard to imagine such a world; we live on one. The surface of the world is curved, which is why it's impossible to make a perfectly accurate flat map of the world. Non-Cartesian coordinate systems illustrate this well; for example, in the spherical coordinates (r, θ, φ), the Euclidean distance can be written
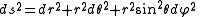
Another illustration would be a world in which the rulers used to measure length were untrustworthy, rulers that changed their length with their position and even their orientation. In the most general case, one must allow for cross-terms when calculating the distance ds
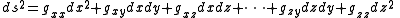
where the nine functions gxx, gxy constitute the metric tensor
, which defines the geometry of the space in Riemannian geometry
. In the spherical-coordinates example above, there are no cross-terms; the only nonzero metric tensor components are grr = 1, gθθ = r2 and gφφ = r2 sin2 θ.
In his special theory of relativity
, Albert Einstein
showed that the distance ds between two spatial points is not constant, but depends on the motion of the observer. However, there is a measure of separation between two points in space-time — called "proper time" and denoted with the symbol dτ — that is invariant; in other words, it doesn't depend on the motion of the observer.
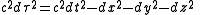
which may be written in spherical coordinates as
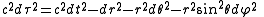
This formula is the natural extension of the Pythagorean theorem
and similarly holds only when there is no curvature in space-time. In general relativity
, however, space and time may have curvature, so this distance formula must be modified to a more general form
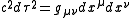
just as we generalized the formula to measure distance on the surface of the Earth. The exact form of the metric gμν depends on the gravitating mass, momentum and energy, as described by the Einstein field equations
. Einstein developed those field equations to match the then known laws of Nature; however, they predicted never-before-seen phenomena (such as the bending of light by gravity) that were confirmed later.
s in the space-time. In uncurved space-time, far from a source of gravity, these geodesics correspond to straight lines; however, they may deviate from straight lines when the space-time is curved. The equation for the geodesic lines is
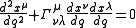
where Γ represents the Christoffel symbol and the variable q parametrizes the particle's path through space-time, its so-called world line
. The Christoffel symbol depends only on the metric tensor
gμν, or rather on how it changes with position. The variable q is a constant multiple of the proper time
τ for timelike orbits (which are traveled by massive particles), and is usually taken to be equal to it. For lightlike (or null) orbits (which are traveled by massless particles such as the photon
), the proper time is zero and, strictly speaking, cannot be used as the variable q. Nevertheless, lightlike orbits can be derived as the ultrarelativistic limit
of timelike orbits, that is, the limit as the particle mass m goes to zero while holding its total energy
fixed.
is the Schwarzschild metric
, which corresponds to the external gravitational field of a stationary, uncharged, non-rotating, spherically symmetric body of mass M. It is characterized by a length scale rs, known as the Schwarzschild radius
, which is defined by the formula
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, as described by the field equations of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
orbiting its sun. Solutions are also used to describe the motion of binary star
Binary star
A binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
s around each other, and estimate their gradual loss of energy through gravitational radiation. It is customary to assume that both bodies are point-like, so that tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
s and the specifics of their material composition can be neglected.
General relativity describes the gravitational field by curved space-time; the field equations governing this curvature are nonlinear and therefore difficult to solve in a closed form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
. Only one exact solution, the Schwarzschild solution
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
, has been found for the Kepler problem; this solution pertains when the mass M of one body is overwhelmingly greater than the mass m of the other. If so, the larger mass may be taken as stationary and the sole contributor to the gravitational field. This is a good approximation for a photon passing a star and for a planet orbiting its sun. The motion of the lighter body (called the "particle" below) can then be determined from the Schwarzschild solution; the motion is a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
("shortest path between two points") in the curved space-time. Such geodesic solutions account for the anomalous precession of the planet Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
, which is a key piece of evidence supporting the theory of general relativity. They also describe the bending of light in a gravitational field, another prediction famously used as evidence for general relativity.
If both masses are considered to contribute to the gravitational field, as in binary stars, the Kepler problem can be solved only approximately. The earliest approximation method to be developed was the post-Newtonian expansion
Post-Newtonian expansion
Post-Newtonian expansions in general relativity are used for finding an approximate solution of the Einstein equations for the metric tensor. The post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of matter, forming the gravitational field, to the...
, an iterative method in which an initial solution is gradually corrected. More recently, it has become possible to solve Einstein's field equation using a computer instead of mathematical formulae. As the two bodies orbit each other, they will emit gravitational radiation
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
; this causes them to lose energy and angular momentum gradually, as illustrated by the binary pulsar PSR B1913+16.
Classical Kepler problem
The Kepler problem derives its name from Johannes KeplerJohannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, who worked as an assistant to the Danish astronomer Tycho Brahe
Tycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
. Brahe took extraordinarily accurate measurements of the motion of the planets of the Solar System. From these measurements, Kepler was able to formulate Kepler's laws
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
, the first modern description of planetary motion:
- The orbitOrbitIn physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
of every planetPlanetA planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
is an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
with the Sun at one of the two fociFocus (geometry)In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
. - A lineLine (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
joining a planet and the Sun sweeps out equal areaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
s during equal intervals of time. - The square of the orbital periodOrbital periodThe orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
of a planet is directly proportionalProportionality (mathematics)In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the cubeCube (arithmetic)In arithmetic and algebra, the cube of a number n is its third power — the result of the number multiplying by itself three times:...
of the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of its orbit.
Kepler published the first two laws in 1609 and the third law in 1619. They supplanted earlier models of the Solar System, such as those of Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
and Copernicus. Kepler's laws apply only in the limited case of the two-body problem. Voltaire
Voltaire
François-Marie Arouet , better known by the pen name Voltaire , was a French Enlightenment writer, historian and philosopher famous for his wit and for his advocacy of civil liberties, including freedom of religion, free trade and separation of church and state...
and Émilie du Châtelet
Émilie du Châtelet
-Early life:Du Châtelet was born on 17 December 1706 in Paris, the only daughter of six children. Three brothers lived to adulthood: René-Alexandre , Charles-Auguste , and Elisabeth-Théodore . Her eldest brother, René-Alexandre, died in 1720, and the next brother, Charles-Auguste, died in 1731...
were the first to call them "Kepler's laws".
Nearly a century later, Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
had formulated his three laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
. In particular, Newton's second law states that a force F applied to a mass m produces an acceleration a given by the equation F=ma. Newton then posed the question: what must the force be that produces the elliptical orbits seen by Kepler? His answer came in his law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
, which states that the force between a mass M and another mass m is given by the formula
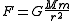,where r is the distance between the masses and G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. Given this force law and his equations of motion, Newton was able to show that two point masses attracting each other would each follow perfectly elliptical orbits. The ratio of sizes of these ellipses is m/M, with the larger mass moving on a smaller ellipse. If M is much larger than m, then the larger mass will appear to be stationary at the focus of the elliptical orbit of the lighter mass m. This model can be applied approximately to the Solar System. Since the mass of the Sun is much larger than those of the planets, the force acting on each planet is principally due to the Sun; the gravity of the planets for each other can be neglected to first approximation.
Apsidal precession
Apsidal precession
In celestial mechanics, perihelion precession, apsidal precession or orbital precession is the precession of the orbit of a celestial body. More precisely it is the gradual rotation of the line joining the apsides of an orbit, which are the points of closest and farthest approach...
is observed for all the planets orbiting the Sun, primarily due to the oblateness of the Sun (it is not perfectly spherical) and the attractions of the other planets for one another. The apsides are the two points of closest and furthest distance of the orbit (the periapsis and apoapsis, respectively); apsidal precession corresponds to the rotation of the line joining the apsides. It also corresponds to the rotation of the Laplace–Runge–Lenz vector, which points along the line of apsides.
Newton's law of gravitation soon became accepted because it gave very accurate predictions of the apsidal precessions of all the planets. These calculations were carried out initially by Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
in the late 18th century, and refined by Félix Tisserand
Félix Tisserand
François Félix Tisserand was a French astronomer.Tisserand was born at Nuits-Saint-Georges, Côte-d'Or. In 1863 he entered the École Normale Supérieure, and on leaving he went for a month as professor at the lycée at Metz. Urbain Le Verrier offered him a post in the Paris Observatory, which he...
in the later 19th century. Conversely, if Newton's law of gravitation had not predicted the apsidal precessions of the planets accurately, it would have to be discarded as a theory of gravitation. Such an anomalous precession was observed in the second half of the 19th century, and it led to the overthrow of Newtonian model of gravity and the development of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
Anomalous precession of Mercury
In 1859, Urbain Le Verrier discovered that the orbital precessionPrecession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of the planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
was not quite what it should be; the ellipse of its orbit was rotating (precessing) slightly faster than predicted by the traditional theory of Newtonian gravity, even after all the effects of the other planets had been accounted for. The effect is small (roughly 43 arcseconds of rotation per century), but well above the measurement error (roughly 0.1 arcseconds per century). Le Verrier realized the importance of his discovery immediately, and challenged astronomers and physicists alike to account for it. Several classical explanations were proposed, such as interplanetary dust, unobserved oblateness of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, an undetected moon of Mercury, or a new planet named Vulcan. After these explanations were discounted, some physicists were driven to the more radical hypothesis that Newton's
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
of gravitation was incorrect. For example, some physicists proposed a power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
with an exponent that was slightly different from 2.
Others argued that Newton's law should be supplemented with a velocity-dependent potential. However, this implied a conflict with newtonian celestial dynamics. In his treatise on celestial mechanics, Laplace had shown that if the gravitational influence does not act instantaneously, then the motions of the planets themselves will not exactly conserve momentum (some of the momentum must then be ascribed to the mediator of the gravitational interaction, analogous to ascribing momentum to the mediator of the electromagnetic interaction.) As seen from a newtonian point of view, if gravitational influence does propagate at a finite speed, then at all points in time a planet is attracted to a point where the Sun was some time before, and not towards the instantaneous position of the Sun. On the assumption of the classical fundamentals, Laplace had shown that if gravity would propagate at a velocity in the order of the speed of light then the solar system would be unstable, and would not exist for a long time. The observation that the solar system is old allows one to put a lower limit on the speed of gravity
Speed of gravity
In the context of classical theories of gravitation, the speed of gravity is the speed at which changes in a gravitational field propagate. This is the speed at which a change in the distribution of energy and momentum of matter results in subsequent alteration, at a distance, of the gravitational...
that is many orders of magnitude faster than the speed of light. Laplace's estimate for the velocity of gravity is not correct, because in a field theory which respects the principle of relativity, the attraction of a point charge which is moving at a constant velocity is towards the extrapolated instantaneous position, not to the apparent position it seems to occupy when looked atFeynman Lectures on Physics vol. II gives a thorough treatment of the analogous problem in electromagnetism. Feynman shows that for a moving charge, the non-radiative field is an attraction/repulsion not toward the apparent position of the particle, but toward the extrapolated position assuming that the particle continues in a straight line in a constant velocity. This is a notable property of the Liénard-Wiechert Potentials
Liénard-Wiechert Potentials
Liénard-Wiechert potentials describe the classical electromagnetic effect of a moving electric point charge in terms of a vector potential and a scalar potential...
which are used in the Wheeler-Feynman absorber theory. Presumably the same holds in linearized gravity.
To avoid those problems, between 1870 and 1900 many scientists used the electrodynamic laws of Wilhelm Eduard Weber
Wilhelm Eduard Weber
Wilhelm Eduard Weber was a German physicist and, together with Carl Friedrich Gauss, inventor of the first electromagnetic telegraph.-Early years:...
, Carl Friedrich Gauß, Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
to produce stable orbits and to explain the Perihelion shift of Mercury's orbit. In 1890 Lévy succeeded in doing so by combining the laws of Weber and Riemann, whereby the speed of gravity
Speed of gravity
In the context of classical theories of gravitation, the speed of gravity is the speed at which changes in a gravitational field propagate. This is the speed at which a change in the distribution of energy and momentum of matter results in subsequent alteration, at a distance, of the gravitational...
is equal to the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in his theory. And in another attempt Paul Gerber
Paul Gerber
Paul Gerber was a German physicist. He studied in Berlin from 1872-1875. In 1877 he became a teacher at the Realgymnasium in Stargard in Pommern...
(1898) even succeeded in deriving the correct formula for the Perihelion shift (which was identical to that formula later used by Einstein). However, because the basic laws of Weber and others were wrong (for example, Weber's law was superseded by Maxwell's theory), those hypotheses were rejected. Another attempt by Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
(1900), who already used Maxwell's theory, produced a Perihelion shift which was too low.
Einstein's theory of general relativity
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
, Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
and finally Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's special theory of relativity, exclude the possibility of propagation of any effects faster than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. It followed that Newton's law of gravitation would have to be replaced with another law, compatible with the principle of relativity, while still obtaining the newtonian limit for circumstances where relativistic effects are negligible. Such attempts were made by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
(1905), Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
(1907) and Arnold Sommerfeld
Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
(1910). In 1907 Einstein came to the conclusion that to achieve this a successor to special relativity was needed. From 1907 to 1915, Einstein worked towards a new theory, using his Equivalence Principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
as a key concept to guide his way. According to this principle, a uniform gravitational field acts equally on everything within it and, therefore, cannot be detected by a free-falling observer. Conversely, all local gravitational effects should be reproducible in a linearly accelerating reference frame, and vice versa. Thus, gravity acts like a fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
such as the centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
or the Coriolis force, which result from being in an accelerated reference frame; all fictitious forces are proportional to the inertial mass, just as gravity is. To effect the reconciliation of gravity and special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and to incorporate the equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
, something had to be sacrificed; that something was the long-held classical assumption that our space obeys the laws of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, e.g., that the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
is true experimentally. Einstein used a more general geometry, pseudo-Riemannian geometry
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, to allow for the curvature of space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
that was necessary for the reconciliation; after eight years of work (1907–1915), he succeeded in discovering the precise way in which space-time should be curved in order to reproduce the physical laws observed in Nature, particularly gravitation. Gravity is distinct from the fictitious forces centrifugal force and coriolis force in the sense that the curvature of spacetime is regarded as physically real, whereas the fictitious forces are not regarded as forces. The very first solutions of his field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
explained the anomalous precession of Mercury and predicted an unusual bending of light, which was confirmed after his theory was published. These solutions are explained below.
General relativity, special relativity and geometry
In the normal Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, triangles obey the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, which states that the square distance ds2 between two points in space is the sum of the squares of its perpendicular components
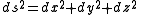
where dx, dy and dz represent the infinitesimal differences between the two points along the x, y and z axes of a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
(add Figure here). Now imagine a world in which this is not quite true; a world where the distance is instead given by
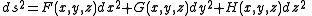
where F, G and H are arbitrary functions of position. It is not hard to imagine such a world; we live on one. The surface of the world is curved, which is why it's impossible to make a perfectly accurate flat map of the world. Non-Cartesian coordinate systems illustrate this well; for example, in the spherical coordinates (r, θ, φ), the Euclidean distance can be written
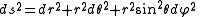
Another illustration would be a world in which the rulers used to measure length were untrustworthy, rulers that changed their length with their position and even their orientation. In the most general case, one must allow for cross-terms when calculating the distance ds
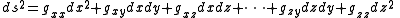
where the nine functions gxx, gxy constitute the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, which defines the geometry of the space in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
. In the spherical-coordinates example above, there are no cross-terms; the only nonzero metric tensor components are grr = 1, gθθ = r2 and gφφ = r2 sin2 θ.
In his special theory of relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
showed that the distance ds between two spatial points is not constant, but depends on the motion of the observer. However, there is a measure of separation between two points in space-time — called "proper time" and denoted with the symbol dτ — that is invariant; in other words, it doesn't depend on the motion of the observer.
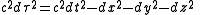
which may be written in spherical coordinates as
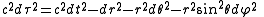
This formula is the natural extension of the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
and similarly holds only when there is no curvature in space-time. In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, however, space and time may have curvature, so this distance formula must be modified to a more general form
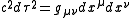
just as we generalized the formula to measure distance on the surface of the Earth. The exact form of the metric gμν depends on the gravitating mass, momentum and energy, as described by the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
. Einstein developed those field equations to match the then known laws of Nature; however, they predicted never-before-seen phenomena (such as the bending of light by gravity) that were confirmed later.
Geodesic equation
According to Einstein's theory of general relativity, particles of negligible mass travel along geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s in the space-time. In uncurved space-time, far from a source of gravity, these geodesics correspond to straight lines; however, they may deviate from straight lines when the space-time is curved. The equation for the geodesic lines is
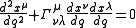
where Γ represents the Christoffel symbol and the variable q parametrizes the particle's path through space-time, its so-called world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
. The Christoffel symbol depends only on the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
gμν, or rather on how it changes with position. The variable q is a constant multiple of the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
τ for timelike orbits (which are traveled by massive particles), and is usually taken to be equal to it. For lightlike (or null) orbits (which are traveled by massless particles such as the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
), the proper time is zero and, strictly speaking, cannot be used as the variable q. Nevertheless, lightlike orbits can be derived as the ultrarelativistic limit
Ultrarelativistic limit
In physics, a particle is called ultrarelativistic when its speed is very close to the speed of light c.Max Planck showed that the relativistic expression for the energy of a particle whose rest mass is m and momentum is p is given by E^2 = m^2 c^4 + p^2 c^2...
of timelike orbits, that is, the limit as the particle mass m goes to zero while holding its total energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
fixed.
Schwarzschild solution
An exact solution to the Einstein field equationsEinstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
is the Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
, which corresponds to the external gravitational field of a stationary, uncharged, non-rotating, spherically symmetric body of mass M. It is characterized by a length scale rs, known as the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
, which is defined by the formula
-
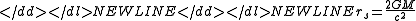
where G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. The classical Newtonian theory of gravity is recovered in the limit as the ratio rs/r goes to zero. In that limit, the metric returns to that defined by special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
In practice, this ratio is almost always extremely small. For example, the Schwarzschild radius rs of the EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is roughly 9 mm ( inchInchAn inch is the name of a unit of length in a number of different systems, including Imperial units, and United States customary units. There are 36 inches in a yard and 12 inches in a foot...
); at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The Schwarzschild radius of the Sun is much larger, roughly 2953 meters, but at its surface, the ratio rs/r is roughly 4 parts in a million. A white dwarfWhite dwarfA white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
star is much denser, but even here the ratio at its surface is roughly 250 parts in a million. The ratio only becomes large close to ultra-dense objects such as neutron starNeutron starA neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s (where the ratio is roughly 50%) and black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s.
Orbits about the central mass
The orbits of a test particle of infinitesimal mass m about the central mass M is given by the equation of motion
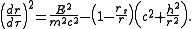
which can be converted into an equation for the orbit
where, for brevity, two length-scales, a and b, have been introduced. They are constants of the motion and depend on the initial conditions (position and velocity) of the test particle. Hence, the solution of the orbit equation is
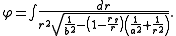
Bending of light by gravity
The orbit of photons and particles moving close to the speed of light (ultrarelativistic particles) is obtained by taking the limit as the length-scale a goes to infinity. In this limit, the equation for the orbit becomes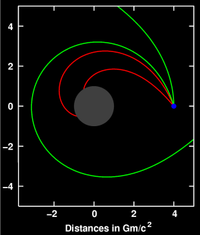
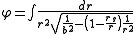
Expanding in powers of rs/r, the leading order term in this formula gives the approximate angular deflection δφ for a massless particle coming in from infinity and going back out to infinity:
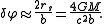
Here, the length-scale b can be interpreted as the distance of closest approach. Although this formula is approximate, it is accurate for most measurements of gravitational lensing, due to the smallness of the ratio rs/r. For light grazing the surface of the sun, the approximate angular deflection is roughly 1.75 arcsecondsMinute of arcA minute of arc, arcminute, or minute of angle , is a unit of angular measurement equal to one sixtieth of one degree. In turn, a second of arc or arcsecond is one sixtieth of one minute of arc....
, roughly one millionth part of a circle.
Effective radial potential energy
The equation of motion for the particle derived above
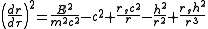
can be rewritten using the definition of the Schwarzschild radiusSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
rs as
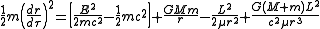
which is equivalent to a particle moving in a one-dimensional effective potentialEffective potentialThe effective potential, or effective potential energy is a mathematical expression combining the centrifugal potential energy with the potential energy of a dynamical system. Commonly used in calculating the orbits of planets , the effective potential allows one to reduce a problem to fewer...
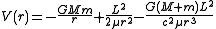
The first two terms are well-known classical energies, the first being the attractive Newtonian gravitational potential energy and the second corresponding to the repulsive "centrifugal" potential energyCentrifugal forceCentrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
; however, the third term is an attractive energy unique to general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. As shown below and elsewhere, this inverse-cubic energy causes elliptical orbits to precess gradually by an angle δφ per revolution
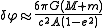
where A is the semi-major axis and e is the eccentricity.
The third term is attractive and dominates at small r values, giving a critical inner radius rinner at which a particle is drawn inexorably inwards to r=0; this inner radius is a function of the particle's angular momentum per unit mass or, equivalently, the a length-scale defined above.
Circular orbits and their stability
The effective potential V can be re-written in terms of the lengths a and b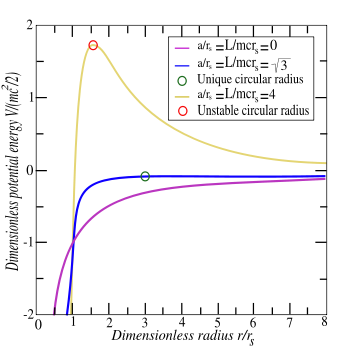
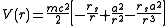
Circular orbits are possible when the effective force is zero
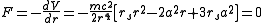
i.e., when the two attractive forces — Newtonian gravity (first term) and the attraction unique to general relativity (third term) — are exactly balanced by the repulsive centrifugal force (second term). There are two radii at which this balancing can occur, denoted here as rinner and router
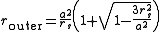
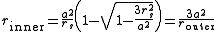
which are obtained using the quadratic formula. The inner radius rinner is unstable, because the attractive third force strengthens much faster than the other two forces when r becomes small; if the particle slips slightly inwards from rinner (where all three forces are in balance), the third force dominates the other two and draws the particle inexorably inwards to r=0. At the outer radius, however, the circular orbits are stable; the third term is less important and the system behaves more like the non-relativistic Kepler problemKepler problemIn classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
.
When a is much greater than rs (the classical case), these formulae become approximately
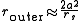
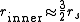
Substituting the definitions of a and rs into router yields the classical formula for a particle orbiting a mass M in a circle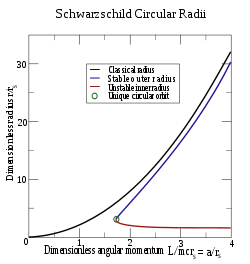
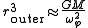
where ωφ is the orbital angular speed of the particle. This formula is obtained in non-relativistic mechanics by setting the centrifugal forceCentrifugal forceCentrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
equal to the Newtonian gravitational force:
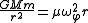
Where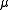
is the reduced massReduced massReduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
.
In our notation, the classical orbital angular speed equals
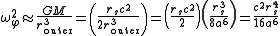
At the other extreme, when a2 approaches 3rs2 from above, the two radii converge to a single value
The quadratic solutions above ensure that router is always greater than 3rs, whereas rinner lies between rs and 3rs. Circular orbits smaller than rs are not possible. For massless particles, a goes to infinity, implying that there is a circular orbit for photons at rinner = rs. The sphere of this radius is sometimes known as the photon sphere.
Precession of elliptical orbits
The orbital precession rate may be derived using this radial effective potential V. A small radial deviation from a circular orbit of radius router will oscillate stably with an angular frequency
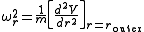
which equals
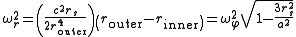
Taking the square root of both sides and expanding using the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
yields the formula
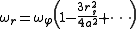
Multiplying by the period T of one revolution gives the precession of the orbit per revolution
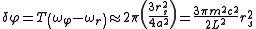
where we have used ωφT = 2п and the definition of the length-scale a. Substituting the definition of the Schwarzschild radiusSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
rs gives
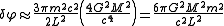
This may be simplified using the elliptical orbit's semiaxis A and eccentricity e related by the formula
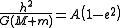
to give the precession angle
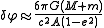
Post-Newtonian expansion
In the Schwarzschild solution, it is assumed that the larger mass M is stationary and it alone determines the gravitational field (i.e., the geometry of space-time) and, hence, the lesser mass m follows a geodesic path through that fixed space-time. This is a reasonable approximation for photons and the orbit of Mercury, which is roughly 6 million times lighter than the Sun. However, it is inadequate for binary starBinary starA binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
s, in which the masses may be of similar magnitude.
The metric for the case of two comparable masses cannot be solved in closed form and therefore one has to resort to approximation techniques such as the post-Newtonian approximation or numerical approximations. In passing, we mention one particular exception in lower dimensions (see R=T model for details). In (1+1) dimensions, i.e. a space made of one spatial dimension and one time dimension, the metric for two bodies of equal masses can be solved analytically in terms of the Lambert W function. However, the gravitational energy between the two bodies is exchanged via dilatonsDilatonIn particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
rather than gravitons which require three-space in which to propagate.
The post-Newtonian expansionPost-Newtonian expansionPost-Newtonian expansions in general relativity are used for finding an approximate solution of the Einstein equations for the metric tensor. The post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of matter, forming the gravitational field, to the...
is a calculational method that provides a series of ever more accurate solutions to a given problem. The method is iterative; an initial solution for particle motions is used to calculate the gravitational fields; from these derived fields, new particle motions can be calculated, from which even more accurate estimates of the fields can be computed, and so on. This approach is called "post-Newtonian" because the Newtonian solution for the particle orbits is often used as the initial solution.
When this method is applied to the two-body problem without restriction on their masses, the result is remarkably simple. To the lowest order, the relative motion of the two particles is equivalent to the motion of an infinitesimal particle in the field of their combined masses. In other words, the Schwarzschild solution can be applied, provided that the M + m is used in place of M in the formulae for the Schwarzschild radius rs and the precession angle per revolution δφ.
Modern computational approaches
Einstein's equations can also be solved on a computer using sophisticated numerical methods. Given sufficient computer power, such solutions can be more accurate than post-Newtonian solutions. However, such calculations are demanding because the equations must generally be solved in a four-dimensional space. Nevertheless, beginning in the late 1990s, it became possible to solve difficult problems such as the merger of two black holes, which is a very difficult version of the Kepler problem in general relativity.
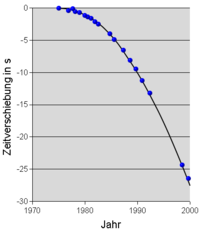
Gravitational radiation
If there is no incoming gravitational radiation, according to general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, two bodies revolving about one another will emit gravitational radiation, causing the orbits to gradually lose energy. This has been observed indirectly in a binary starBinary starA binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
system known as PSR B1913+16, for which Russell Alan HulseRussell Alan HulseRussell Alan Hulse is an American physicist and winner of the Nobel Prize in Physics, shared with his thesis advisor Joseph Hooton Taylor Jr., "for the discovery of a new type of pulsar, a discovery that has opened up new possibilities for the study of gravitation"...
and Joseph Hooton Taylor, Jr.Joseph Hooton Taylor, Jr.Joseph Hooton Taylor, Jr. is an American astrophysicist and Nobel Prize in Physics laureate for his discovery with Russell Alan Hulse of a "new type of pulsar, a discovery that has opened up new possibilities for the study of gravitation."...
were awarded the 1993 Nobel Prize in PhysicsNobel Prize in PhysicsThe Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
. The two neutron starNeutron starA neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s of this system are extremely close and rotate about one another very quickly, completing a revolution in roughly 465 minutes. Their orbit is highly elliptical, with an eccentricityOrbital eccentricityThe orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
of 0.62 (62%). According to general relativity, the short orbital periodOrbital periodThe orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
and high eccentricity should make the system an excellent emitter of gravitational radiation, thereby losing energy and decreasing the orbital period still further. The observed decrease in the orbital period over thirty years matches the predictions of general relativity within even the most precise measurements. General relativity predicts that, in another 300 million years, these two stars will spiral into one another.
The formulae describing the loss of energy
EnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
due to gravitational radiation from the two bodies of the Kepler problem have been calculated. The rate of losing energy (averaged over a complete orbit) is given by
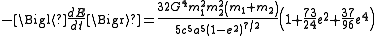
where e is the orbital eccentricityOrbital eccentricityThe orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
and a is the semimajor axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the ellipticalEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
orbit. The angular brackets on the left-hand side of the equation represent the averaging over a single orbit. Similarly, the average rate of losing angular momentum equals
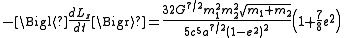
The losses in energy and angular momentum increase significantly as the eccentricity approaches one, i.e., as the ellipse of the orbit becomes ever more elongated. The radiation losses also increase significantly with a decreasing size a of the orbit.
External links