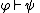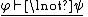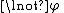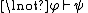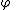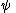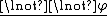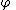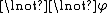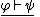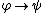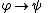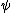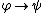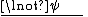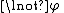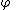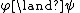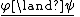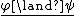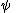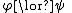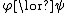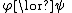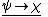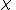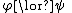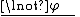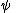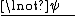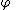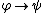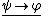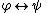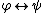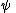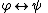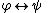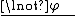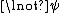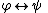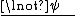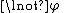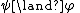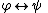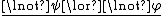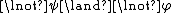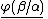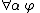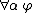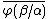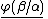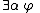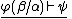List of rules of inference
Encyclopedia
This is a list of rules of inference
, logical laws that relate to mathematical formulae.
Discharge rules permit inference from a subderivation based on a temporary assumption. Below, the notation
indicates such a subderivation from the temporary assumption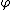 to
to 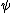 .
.
.
(or Negation Introduction):
Reductio ad absurdum (related to the law of excluded middle):
Noncontradiction (or Negation Elimination):
Double negation elimination
:
Double negation introduction:
(or Conditional Introduction
):
Modus ponens
(or Conditional Elimination):
Modus tollens
:
(or Conjunction Introduction):
Simplification
(or Conjunction Elimination):
Case analysis
Disjunctive syllogism
:
:
Biconditional Elimination:
Rules of classical predicate calculus
In the following rules, 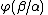 is exactly like
is exactly like 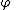 except for having the term
except for having the term 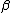 everywhere
everywhere 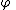 has the free variable
has the free variable 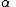 .
.
Universal Introduction (or Universal Generalization):
Restriction 1: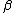 does not occur in
does not occur in  .
.
Restriction 2: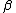 is not mentioned in any hypothesis or undischarged assumptions.
is not mentioned in any hypothesis or undischarged assumptions.
Universal Elimination
(or Universal Instantiation):
Restriction: No free occurrence of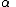 in
in 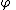 falls within the scope of a quantifier quantifying a variable occurring in
falls within the scope of a quantifier quantifying a variable occurring in 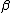 .
.
Existential Introduction (or Existential Generalization):
Restriction: No free occurrence of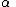 in
in 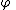 falls within the scope of a quantifier quantifying a variable occurring in
falls within the scope of a quantifier quantifying a variable occurring in 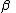 .
.
Existential Elimination (or Existential Instantiation):
Restriction 1: No free occurrence of in
in 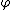 falls within the scope of a quantifier quantifying a variable occurring in
falls within the scope of a quantifier quantifying a variable occurring in 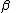 .
.
Restriction 2: There is no occurrence, free or bound, of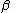 in
in 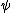 .
.
" column shows how to interpret the notation of a given rule.
All rules use the basic logic operators. A complete table of "logic operators" is showed by a truth table
, giving definitions of all the possible (16) truth functions of 2 boolean variables (p, q):
where T = true and F = false, and, the columns are the logical operators: 0, false, Contradiction
; 1, NOR, Logical NOR
; 2, Converse nonimplication; 3, ¬p, Negation
; 4, Material nonimplication
; 5, ¬q, Negation; 6, XOR, Exclusive disjunction
; 7, NAND, Logical NAND; 8, AND, Logical conjunction
; 9, XNOR, If and only if
, Logical biconditional
; 10, q, Projection function; 11, if/then, Logical implication; 12, p, Projection function; 13, then/if, Converse implication
; 14, OR, Logical disjunction
; 15, true, Tautology
.
Each logic operator can be used in a assertion about variables and operations, showing a basic rule of inference. Examples:
Machines and well-trained people use this look at table approach
to do basic inferences, and to check if other inferences (for the same premises) can be obtained.
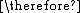 ), if it rains today, we will go on a canoe trip tomorrow.
), if it rains today, we will go on a canoe trip tomorrow.
To make use of the rules of inference in the above table we let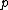 be the proposition "If it rains today",
be the proposition "If it rains today", 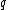 be " We will not go on a canoe today" and let
be " We will not go on a canoe today" and let  be "We will go on a canoe trip tomorrow". Then this argument is of the form:
be "We will go on a canoe trip tomorrow". Then this argument is of the form:
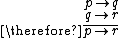
Proof by rules of inference: Let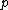 be the proposition "It is sunny this today",
be the proposition "It is sunny this today", 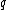 the proposition "It is colder than yesterday",
the proposition "It is colder than yesterday",  the proposition "We will go swimming",
the proposition "We will go swimming",  the proposition "We will have a barbecue", and
the proposition "We will have a barbecue", and  the proposition "We will be home by sunset". Then the hypotheses become
the proposition "We will be home by sunset". Then the hypotheses become  and
and 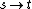 . Using our intuition we conjecture that the conclusion might be
. Using our intuition we conjecture that the conclusion might be  . Using the Rules of Inference table we can proof the conjecture easily:
. Using the Rules of Inference table we can proof the conjecture easily:
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
, logical laws that relate to mathematical formulae.
Introduction
Rules of inference are syntactical transform rules which one can use to infer a conclusion from a premise to create an argument. A set of rules can be used to infer any valid conclusion if it is complete, while never inferring an invalid conclusion, if it is sound. A sound and complete set of rules need not include every rule in the following list, as many of the rules are redundant, and can be proven with the other rules.Discharge rules permit inference from a subderivation based on a temporary assumption. Below, the notation
indicates such a subderivation from the temporary assumption
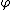 to
to 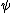 .
.Rules for classical sentential calculus
Sentential calculus is also known as propositional calculusPropositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
.
Rules for negations
Reductio ad absurdumReductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
(or Negation Introduction):
Reductio ad absurdum (related to the law of excluded middle):
Noncontradiction (or Negation Elimination):
Double negation elimination
Double negative elimination
In propositional logic, the inference rules double negative elimination allow deriving the double negative equivalent by adding or removing a pair of negation signs...
:
Double negation introduction:
Rules for conditionals
Deduction theoremDeduction theorem
In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
(or Conditional Introduction
Conditional proof
A conditional proof is a proof that takes the form of asserting a conditional, and proving that the antecedent of the conditional necessarily leads to the consequent....
):
Modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
(or Conditional Elimination):
Modus tollens
Modus tollens
In classical logic, modus tollens has the following argument form:- Formal notation :...
:
Rules for conjunctions
AdjunctionConjunction introduction
Conjunction introduction is the inference that, if p is true, and q is true, then the conjunction p and q is true.For example, if it's true that it's raining, and it's true that I'm inside, then it's true that "it's raining and I'm inside"....
(or Conjunction Introduction):
Simplification
Simplification (logic)
In mathematical logic, simplification is a valid argument and rule of inference which makes the inference that, if the conjunction A and B is true, then A is true, and B is true.In formal language:...
(or Conjunction Elimination):
Rules for disjunctions
Addition (or Disjunction Introduction):Case analysis
Case analysis
Case analysis is one of the most general and applicable methods of analytical thinking, depending only on the division of a problem, decision or situation into a sufficient number of separate cases. Analysing each such case individually may be enough to resolve the initial question...
Disjunctive syllogism
Disjunctive syllogism
A disjunctive syllogism, also known as disjunction-elimination and or-elimination , and historically known as modus tollendo ponens,, is a classically valid, simple argument form:where \vdash represents the logical assertion....
:
Rules for biconditionals
Biconditional introductionBiconditional introduction
In mathematical logic, biconditional introduction is the rule of inference that, if B follows from A, and A follows from B, then A if and only if B....
:
Biconditional Elimination:
Rules of classical predicate calculusFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
In the following rules, 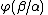 is exactly like
is exactly like 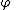 except for having the term
except for having the term 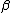 everywhere
everywhere 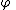 has the free variable
has the free variable 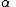 .
.Universal Introduction (or Universal Generalization):
Restriction 1:
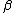 does not occur in
does not occur in  .
.Restriction 2:
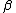 is not mentioned in any hypothesis or undischarged assumptions.
is not mentioned in any hypothesis or undischarged assumptions.Universal Elimination
Universal instantiation
In logic universal instantiation is an inference from a truth about each member of a class of individuals to the truth about a particular individual of that class. It is generally given as a quantification rule for the universal quantifier but it can also be encoded in an axiom...
(or Universal Instantiation):
Restriction: No free occurrence of
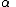 in
in 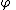 falls within the scope of a quantifier quantifying a variable occurring in
falls within the scope of a quantifier quantifying a variable occurring in 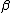 .
.Existential Introduction (or Existential Generalization):
Restriction: No free occurrence of
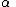 in
in 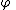 falls within the scope of a quantifier quantifying a variable occurring in
falls within the scope of a quantifier quantifying a variable occurring in 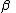 .
.Existential Elimination (or Existential Instantiation):
Restriction 1: No free occurrence of
 in
in 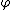 falls within the scope of a quantifier quantifying a variable occurring in
falls within the scope of a quantifier quantifying a variable occurring in 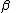 .
.Restriction 2: There is no occurrence, free or bound, of
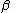 in
in 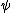 .
.Table: Rules of Inference - a short summary
The rules above can be summed up in the following table. The "TautologyTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
" column shows how to interpret the notation of a given rule.
| Rule of inference | Tautology | Name |
|---|---|---|
 |
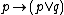 |
Addition |
 |
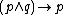 |
Simplification |
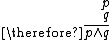 |
 |
Conjunction |
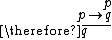 |
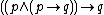 |
Modus ponens Modus ponens In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments... |
 |
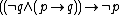 |
Modus tollens Modus tollens In classical logic, modus tollens has the following argument form:- Formal notation :... |
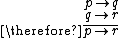 |
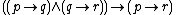 |
Hypothetical syllogism |
 |
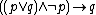 |
Disjunctive syllogism |
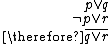 |
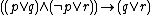 |
Resolution |
All rules use the basic logic operators. A complete table of "logic operators" is showed by a truth table
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
, giving definitions of all the possible (16) truth functions of 2 boolean variables (p, q):
| p | q | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | T | F | F | F | F | F | F | F | F | T | T | T | T | T | T | T | T | ||
| T | F | F | F | F | F | T | T | T | T | F | F | F | F | T | T | T | T | ||
| F | T | F | F | T | T | F | F | T | T | F | F | T | T | F | F | T | T | ||
| F | F | F | T | F | T | F | T | F | T | F | T | F | T | F | T | F | T |
where T = true and F = false, and, the columns are the logical operators: 0, false, Contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
; 1, NOR, Logical NOR
Logical NOR
In boolean logic, logical nor or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form is true precisely when neither p nor q is true—i.e. when both of p and q are false...
; 2, Converse nonimplication; 3, ¬p, Negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
; 4, Material nonimplication
Material nonimplication
Material nonimplication or abjunction is the negation of implication. That is to say that for any two propositions P and Q, if P does not imply Q, then P is the material nonimplication of Q....
; 5, ¬q, Negation; 6, XOR, Exclusive disjunction
Exclusive disjunction
The logical operation exclusive disjunction, also called exclusive or , is a type of logical disjunction on two operands that results in a value of true if exactly one of the operands has a value of true...
; 7, NAND, Logical NAND; 8, AND, Logical conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
; 9, XNOR, If and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
, Logical biconditional
Logical biconditional
In logic and mathematics, the logical biconditional is the logical connective of two statements asserting "p if and only if q", where q is a hypothesis and p is a conclusion...
; 10, q, Projection function; 11, if/then, Logical implication; 12, p, Projection function; 13, then/if, Converse implication
Converse implication
Converse implication is the converse of implication. That is to say; that for any two propositions P and Q, if Q implies P, then P is the converse implication of Q.It may take the following forms:-Truth table:The truth table of A⊂B-Venn diagram:...
; 14, OR, Logical disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
; 15, true, Tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
.
Each logic operator can be used in a assertion about variables and operations, showing a basic rule of inference. Examples:
- The column-14 operator (OR), shows Addition rule: when p=T (the hypothesis selects the first two lines of the table), we see (at column-14) that p∨q=T.
- We can see also that, with the same premise, another conclusions are valid: columns 12, 14 and 15 are T.
- The column-8 operator (AND), shows Simplification rule: when p∧q=T (first line of the table), we see that p=T.
- With this premise, we also conclude that q=T, p∨q=T, etc. as showed by columns 9-15.
- The column-11 operator (IF/THEN), shows Modus ponens rule: when p→q=T and p=T only one line of the truth table (the first) satisfies these two conditions. On this line, q is also true. Therefore, whenever p → q is true and p is true, q must also be true.
Machines and well-trained people use this look at table approach
Lookup table
In computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
to do basic inferences, and to check if other inferences (for the same premises) can be obtained.
Example 1
Let us consider the following assumptions: "If it rains today, then we will not go on a canoe today. If we do not go on a canoe trip today, then we will go on a canoe trip tomorrow. Therefore (Mathematical symbol for "therefore" is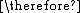 ), if it rains today, we will go on a canoe trip tomorrow.
), if it rains today, we will go on a canoe trip tomorrow.To make use of the rules of inference in the above table we let
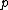 be the proposition "If it rains today",
be the proposition "If it rains today", 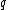 be " We will not go on a canoe today" and let
be " We will not go on a canoe today" and let  be "We will go on a canoe trip tomorrow". Then this argument is of the form:
be "We will go on a canoe trip tomorrow". Then this argument is of the form: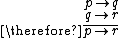
Example 2
Let us consider a more complex set of assumptions: "It is not sunny today and it is colder than yesterday". "We will go swimming only if it is sunny", "If we do not go swimming, then we will have a barbecue", and "If we will have a barbecue, then we will be home by sunset" lead to the conclusion "We will be home before sunset."Proof by rules of inference: Let
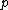 be the proposition "It is sunny this today",
be the proposition "It is sunny this today", 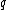 the proposition "It is colder than yesterday",
the proposition "It is colder than yesterday",  the proposition "We will go swimming",
the proposition "We will go swimming",  the proposition "We will have a barbecue", and
the proposition "We will have a barbecue", and  the proposition "We will be home by sunset". Then the hypotheses become
the proposition "We will be home by sunset". Then the hypotheses become  and
and 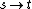 . Using our intuition we conjecture that the conclusion might be
. Using our intuition we conjecture that the conclusion might be  . Using the Rules of Inference table we can proof the conjecture easily:
. Using the Rules of Inference table we can proof the conjecture easily:
| Step | Reason |
|---|---|
1.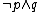 |
Hypothesis |
2. 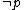 |
Simplification using Step 1 |
3.  |
Hypothesis |
4. 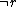 |
Modus tollens using Step 2 and 3 |
5. 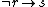 |
Hypothesis |
6.  |
Modus ponens using Step 4 and 5 |
7. 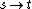 |
Hypothesis |
8.  |
Modus ponens using Step 6 and 7 |