
Mereology
Encyclopedia
In philosophy
and mathematical logic
, mereology (from the Greek μέρος, root: μερε(σ)-, "part" and the suffix -logy "study, discussion, science") treats parts and the wholes they form. Whereas set theory
is founded on the membership relation between a set and its elements, mereology emphasizes the meronomic
relation between entities, which from a set theoretic perspective is closer to that of inclusion between sets.
Mereology has been axiomatized in various ways as applications of predicate logic
to formal ontology
, of which mereology is an important part. A common element of such axiomatizations is the assumption, shared with inclusion, that the part-whole relation partially orders its universe, meaning that everything is a part of itself (reflexivity
), that a part of a part of a whole is itself a part of that whole (transitivity
), and that two distinct entities cannot each be a part of the other (antisymmetry
). A variant of this axiomatization denies that anything is ever part of itself (irreflexive) while accepting transitivity, from which antisymmetry follows automatically.
Standard university texts on logic and mathematics are silent about mereology, which has undoubtedly contributed to its obscurity. Although mereology is an application of mathematical logic
, what can be argued a sort of "proto-geometry", it has been wholly developed by logicians, ontologists
, linguists, engineers, and computer scientists, especially those working in artificial intelligence
.
"Mereology" can also refer to formal work in General Systems Theory on system decomposition and parts, wholes and boundaries (by, e.g., Mihajlo D. Mesarovic
(1970), Gabriel Kron
(1963), or Maurice Jessel (see (Bowden 1989, 1998)). An hierarchical version of Gabriel Kron
's Network Tearing was published by Keith Bowden (1991), reflecting David Lewis's ideas on Gunk
. Such ideas appear in theoretical computer science
and physics
, often in combination with Sheaf, Topos
, or Category Theory
. See also the work of Steve Vickers on (parts of) specifications in Computer Science, Joseph Goguen
on physical systems, and Tom Etter (1996, 1998) on Link Theory and Quantum Mechanics
.
The class concept in object-oriented programming
lends a mereological aspect to programming not found in either imperative programs or declarative programs. Method inheritance
enriches this application of mereology by providing for passing procedural information down the part-whole relation, thereby making method inheritance a naturally arising aspect of mereology.
and ontology
from Plato
(in particular, in the second half of the Parmenides) and Aristotle
onwards, and more or less unwittingly in 19th-century mathematics until the triumph of set theory
around 1910. Ivor Grattan-Guinness
(2001) sheds much light on part-whole reasoning during the 19th and early 20th centuries, and reviews how Cantor
and Peano devised set theory
. It appears that the first to reason consciously and at length about parts and wholes was Edmund Husserl
in his 1901 Logical Investigations (Husserl 1970 is the English translation). However, the word "mereology" is absent from his writings, and he employed no symbolism even though his doctorate was in mathematics.
Stanisław Leśniewski coined "mereology" in 1927, from the Greek word μέρος (méros, "part"), to refer to a formal theory of part-whole he devised in a series of highly technical papers published between 1916 and 1931, and translated in Leśniewski (1992). Leśniewski's student Alfred Tarski
, in his Appendix E to Woodger (1937) and the paper translated as Tarski (1984), greatly simplified Leśniewski's formalism. Other students (and students of students) of Lesniewski elaborated this "Polish mereology" over the course of the 20th century. For a good selection of the literature on Polish mereology, see Srzednicki and Rickey (1984). For a survey of Polish mereology, see Simons (1987). Since 1980 or so, however, research on Polish mereology has been almost entirely historical in nature.
A.N. Whitehead planned a fourth volume of Principia Mathematica
, on geometry
, but never wrote it. His 1914 correspondence with Bertrand Russell
reveals that his intended approach to geometry can be seen, with the benefit of hindsight, as mereological in essence. This work culminated in Whitehead (1916) and the mereological systems of Whitehead (1919, 1920).
In 1930, Henry Leonard completed a Harvard Ph.D. dissertation in philosophy, setting out a formal theory of the part-whole relation. This evolved into the "calculus of individuals" of Goodman and Leonard (1940). Goodman revised and elaborated this calculus in the three editions of Goodman (1951). The calculus of individuals is the starting point for the post-1970 revival of mereology among logicians, ontologists, and computer scientists, a revival well-surveyed in Simons (1987) and Casati and Varzi (1999).
. Doing so gives rise to paradoxes analogous to Russell's paradox
. Let there be an object O such that every object that is not a proper part of itself is a proper part of O. Is O a proper part of itself? No, because no object is a proper part of itself; and yes, because it meets the specified requirement for inclusion as a proper part of O. (Every object is, of course, an improper part of itself. Another, though differently structured, paradox can be made using improper part instead of proper part; and another using improper or proper part.) Hence, mereology requires an axiomatic formulation.
A mereological "system" is a first-order theory
(with identity
) whose universe of discourse consists of wholes and their respective parts, collectively called objects. Mereology is a collection of nested and non-nested axiomatic system
s, not unlike the case with modal logic
.
The treatment, terminology, and hierarchical organization below follow Casati and Varzi (1999: Ch. 3) closely. For a more recent treatment, correcting certain misconceptions, see Hovda (2008). Lower-case letters denote variables ranging over objects. Following each symbolic axiom or definition is the number of the corresponding formula in Casati and Varzi, written in bold.
A mereological system requires at least one primitive binary relation
(dyadic
predicate). The most conventional choice for such a relation is Parthood (also called "inclusion"), "x is a part of y", written Pxy. Nearly all systems require that Parthood partially order the universe. The following defined relations, required for the axioms below, follow immediately from Parthood alone:
Overlap and Underlap are reflexive
, symmetric, and intransitive
.
Systems vary in what relations they take as primitive and as defined. For example, in extensional mereologies (defined below), Parthood can be defined from Overlap as follows: 3.31
3.31
The axioms are:
The systems in the table below are partially ordered by inclusion
, in the sense that, if all the theorems of system A are also theorems of system B, but the converse is not necessarily true, then B includes A. The resulting Hasse diagram
is similar to that in Fig. 2, and Fig. 3.2 in Casati and Varzi (1999: 48).
There are two equivalent ways of asserting that the universe
is partially ordered: Assume either M1–M3, or that Proper Parthood is transitive
and asymmetric
, hence a strict partial order. Either axiomatization results in the system M. M2 rules out closed loops formed using Parthood, so that the part relation is well-founded. Sets are well-founded if the axiom of Regularity
is assumed. The literature contains occasional philosophical and common-sense objections to the transitivity of Parthood.
M4 and M5 are two ways of asserting supplementation, the mereological analog of set complement
ation, with M5 being stronger because M4 is derivable from M5. M and M4 yield minimal mereology, MM. MM, reformulated in terms of Proper Part, is Simons's (1987) preferred minimal system.
In any system in which M5 or M5' are assumed or can be derived, then it can be proved that two objects having the same proper parts are identical. This property is known as Extensionality
, a term borrowed from set theory, for which extensionality
is the defining axiom. Mereological systems in which Extensionality holds are termed extensional, a fact denoted by including the letter E in their symbolic names.
M6 asserts that any two underlapping objects have a unique sum; M7 asserts that any two overlapping objects have a unique product. If the universe is finite or if Top is assumed, then the universe is closed under sum. Universal closure of Product and of supplementation relative to W requires Bottom. W and N are, evidently, the mereological analog of the universal
and empty set
s, and Sum and Product are, likewise, the analogs of set-theoretical union
and intersection
. If M6 and M7 are either assumed or derivable, the result is a mereology with closure.
Because Sum and Product are binary operations, M6 and M7 admit the sum and product of only a finite number of objects. The fusion axiom, M8, enables taking the sum of infinitely many objects. The same holds for Product, when defined. At this point, mereology often invokes set theory
, but any recourse to set theory is eliminable by replacing a formula with a quantified
variable ranging over a universe of sets by a schematic formula with one free variable. The formula comes out true (is satisfied) whenever the name of an object that would be a member of the set (if it existed) replaces the free variable. Hence any axiom with sets can be replaced by an axiom schema
with monadic atomic subformulae. M8 and M8' are schemas of just this sort. The syntax
of a first-order theory can describe only a denumerable number of sets; hence, only denumerably many sets may be eliminated in this fashion, but this limitation is not binding for the sort of mathematics contemplated here.
If M8 holds, then W exists for infinite universes. Hence, Top need be assumed only if the universe is infinite and M8 does not hold. It is interesting to note that Top (postulating W) is not controversial, but Bottom (postulating N) is. Leśniewski rejected Bottom, and most mereological systems follow his example (an exception is the work of Richard Milton Martin
). Hence, while the universe is closed under sum, the product of objects that do not overlap is typically undefined. A system with W but not N is isomorphic to:
Postulating N renders all possible products definable, but also transforms classical extensional mereology into a set-free model
of Boolean algebra.
If sets are admitted, M8 asserts the existence of the fusion of all members of any nonempty set. Any mereological system in which M8 holds is called general, and its name includes G. In any general mereology, M6 and M7 are provable. Adding M8 to an extensional mereology results in general extensional mereology, abbreviated GEM; moreover, the extensionality renders the fusion unique. On the converse, however, if the fusion asserted by M8 is assumed unique, so that M8' replaces M8, then - as Tarski (1929) had shown - M3 and M8' suffice to axiomatize GEM, a remarkably economical result. Simons (1987: 38–41) lists a number of GEM theorems.
M2 and a finite universe necessarily imply Atomicity, namely that everything either is an atom or includes atoms among its proper parts. If the universe is infinite, Atomicity requires M9. Adding M9 to any mereological system, X results in the atomistic variant thereof, denoted AX. Atomicity permits economies, for instance, assuming that M5' implies Atomicity and extensionality, and yields an alternative axiomatization of AGEM.
. For a long time, nearly all philosophers and mathematicians avoided mereology, seeing it as tantamount to a rejection of set theory. Goodman too was a nominalist, and his fellow nominalist Richard Milton Martin
employed a version of the calculus of individuals throughout his career, starting in 1941.
Much early work on mereology was motivated by a suspicion that set theory
was ontologically
suspect, and that Occam's Razor
requires that one minimise the number of posits in one's theory of the world and of mathematics. Mereology replaces talk of "sets" of objects with talk of "sums" of objects, objects being no more than the various things that make up wholes.
Many logicians and philosophers reject these motivations, on such grounds as:
For a survey of attempts to found mathematics without using set theory, see Burgess and Rosen (1997).
In the 1970s, thanks in part to Eberle (1970), it gradually came to be understood that one can employ mereology regardless of one's ontological stance regarding sets. This understanding is called the "ontological innocence" of mereology. This innocence stems from the mereology being formalizable in either of two equivalent ways:
Once it became clear that mereology is not tantamount to a denial of set theory, mereology became largely accepted as a useful tool for formal ontology
and metaphysics
.
In set theory, singletons are "atoms" that have no (non-empty) proper parts; many consider set theory useless or incoherent (not "well-founded") if sets cannot be built up from unit sets. The calculus of individuals was thought to require that an object either have no proper parts, in which case it is an "atom", or be the mereological sum of atoms. Eberle (1970) showed how to construct a calculus of individuals lacking "atoms
", i.e., one where every object has a "proper part" (defined below) so that the universe
is infinite.
There are analogies between the axioms of mereology and those of standard Zermelo-Fraenkel set theory (ZF), if Parthood is taken as analogous to subset
in set theory. On the relation of mereology and ZF, also see Bunt (1985). One of the very few contemporary set theorist to discuss mereology is Potter (2004).
Lewis (1991) went further, showing informally that mereology, augmented by a few ontological
assumptions and plural quantification
, and some novel reasoning about singletons, yields a system in which a given individual can be both a member and a subset of another individual. In the resulting system, the axioms of ZFC (and of Peano arithmetic) are theorems.
Forrest (2002) revises Lewis's analysis by first formulating a generalization of CEM, called "Heyting mereology", whose sole nonlogical primitive is Proper Part, assumed transitive and antireflexive. There exists a "fictitious" null individual that is a proper part of every individual. Two schemas assert that every lattice
join exists (lattices are complete
) and that meet distributes over join. On this Heyting mereology, Forrest erects a theory of pseudosets, adequate for all purposes to which sets have been put.
s using the calculus of individuals, but were mostly unsuccessful; Quine did not reprint that article in his Selected Logic Papers. In a series of chapters in the books he published in the last decade of his life, Richard Milton Martin
set out to do what Goodman and Quine had abandoned 30 years prior. A recurring problem with attempts to ground mathematics in mereology is how to build up the theory of relations
while abstaining from set-theoretic definitions of the ordered pair
. Martin argued that Eberle's (1970) theory of relational individuals solved this problem.
To date, the only persons well trained in mathematics to write on mereology have been Alfred Tarski
and Rolf Eberle. Eberle (1970) clarified the relation between mereology and Boolean algebra, and mereology and set theory. He is one of the very few contributors to mereology to prove sound
and complete each system he describes.
Topological
notions of boundaries
and connection can be married to mereology, resulting in mereotopology
; see Casati and Varzi (1999: chpts. 4,5). Whitehead's 1929 Process and Reality
contains a good deal of informal mereotopology
.
of natural language, shows how mereology can help understand such phenomena as the mass–count distinction
and verb aspect
. But Nicolas (2008) argues that a different logical framework, called plural logic
, should be used for that purpose.
Also, natural language
often employs "part of" in ambiguous ways (Simons 1987 discusses this at length). Hence, it is unclear how, if at all, one can translate certain natural language expressions into mereological predicates. Steering clear of such difficulties may require limiting the interpretation of mereology to mathematics
and natural science
. Casati and Varzi (1999), for example, limit the scope of mereology to physical objects.
Simons devotes considerable effort to elucidating historical notations. The notation of Casati and Varzi is often used. Both books include excellent bibliographies.
To these works should be added Hovda (2008), which presents the latest state of the art on the axiomatization of mereology.
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
and mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, mereology (from the Greek μέρος, root: μερε(σ)-, "part" and the suffix -logy "study, discussion, science") treats parts and the wholes they form. Whereas set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
is founded on the membership relation between a set and its elements, mereology emphasizes the meronomic
Meronomy
A meronomy is a type of hierarchy that deals with part-whole relationships, in contrast to a taxonomy whose categorisation is based on discrete sets. These conceptual structures are used in linguistics and computer science, with applications in biology. The part-whole relationship is sometimes...
relation between entities, which from a set theoretic perspective is closer to that of inclusion between sets.
Mereology has been axiomatized in various ways as applications of predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
to formal ontology
Formal ontology
In philosophy, the term formal ontology is used to refer to an ontology defined by axioms in a formal language with the goal to provide an unbiased view on reality, which can help the modeler of domain- or application-specific ontologies to avoid possibly erroneous ontological assumptions...
, of which mereology is an important part. A common element of such axiomatizations is the assumption, shared with inclusion, that the part-whole relation partially orders its universe, meaning that everything is a part of itself (reflexivity
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
), that a part of a part of a whole is itself a part of that whole (transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
), and that two distinct entities cannot each be a part of the other (antisymmetry
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
). A variant of this axiomatization denies that anything is ever part of itself (irreflexive) while accepting transitivity, from which antisymmetry follows automatically.
Standard university texts on logic and mathematics are silent about mereology, which has undoubtedly contributed to its obscurity. Although mereology is an application of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, what can be argued a sort of "proto-geometry", it has been wholly developed by logicians, ontologists
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
, linguists, engineers, and computer scientists, especially those working in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
.
"Mereology" can also refer to formal work in General Systems Theory on system decomposition and parts, wholes and boundaries (by, e.g., Mihajlo D. Mesarovic
Mihajlo D. Mesarovic
Mihajlo D. Mesarovic , is a Yugoslavian scientist, who is a professor of Systems Engineering and Mathematics at Case Western Reserve University...
(1970), Gabriel Kron
Gabriel Kron
Gabriel Kron was considered an unconventional and somewhat controversial engineer who worked for General Electric in the US from 1934 until 1966. He was responsible for the first load flow distribution system in New York...
(1963), or Maurice Jessel (see (Bowden 1989, 1998)). An hierarchical version of Gabriel Kron
Gabriel Kron
Gabriel Kron was considered an unconventional and somewhat controversial engineer who worked for General Electric in the US from 1934 until 1966. He was responsible for the first load flow distribution system in New York...
's Network Tearing was published by Keith Bowden (1991), reflecting David Lewis's ideas on Gunk
Gunk (mereology)
In mereology, an area of philosophical logic, the term gunk applies to any whole whose parts all have further proper parts. That is, a gunky object is not made of indivisible atoms. In contrast, an atomic individual is entirely decomposable into atoms.If point-sized objects are always simple, then...
. Such ideas appear in theoretical computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, often in combination with Sheaf, Topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, or Category Theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. See also the work of Steve Vickers on (parts of) specifications in Computer Science, Joseph Goguen
Joseph Goguen
Joseph Amadee Goguen was a computer science professor in the Department of Computer Science and Engineering at the University of California, San Diego, USA, who helped develop the OBJ family of programming languages. He was author of A Categorical Manifesto and founder and Editor-in-Chief of the...
on physical systems, and Tom Etter (1996, 1998) on Link Theory and Quantum Mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
The class concept in object-oriented programming
Object-oriented programming
Object-oriented programming is a programming paradigm using "objects" – data structures consisting of data fields and methods together with their interactions – to design applications and computer programs. Programming techniques may include features such as data abstraction,...
lends a mereological aspect to programming not found in either imperative programs or declarative programs. Method inheritance
Inheritance (object-oriented programming)
In object-oriented programming , inheritance is a way to reuse code of existing objects, establish a subtype from an existing object, or both, depending upon programming language support...
enriches this application of mereology by providing for passing procedural information down the part-whole relation, thereby making method inheritance a naturally arising aspect of mereology.
History
Informal part-whole reasoning was consciously invoked in metaphysicsMetaphysics
Metaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
and ontology
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
from Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
(in particular, in the second half of the Parmenides) and Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
onwards, and more or less unwittingly in 19th-century mathematics until the triumph of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
around 1910. Ivor Grattan-Guinness
Ivor Grattan-Guinness
Ivor Grattan-Guinness, born 23 June 1941, in Bakewell, in England, is a historian of mathematics and logic.He gained his Bachelor degree as a Mathematics Scholar at Wadham College, Oxford, got an M.Sc in Mathematical Logic and the Philosophy of Science at the London School of Economics in 1966...
(2001) sheds much light on part-whole reasoning during the 19th and early 20th centuries, and reviews how Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
and Peano devised set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. It appears that the first to reason consciously and at length about parts and wholes was Edmund Husserl
Edmund Husserl
Edmund Gustav Albrecht Husserl was a philosopher and mathematician and the founder of the 20th century philosophical school of phenomenology. He broke with the positivist orientation of the science and philosophy of his day, yet he elaborated critiques of historicism and of psychologism in logic...
in his 1901 Logical Investigations (Husserl 1970 is the English translation). However, the word "mereology" is absent from his writings, and he employed no symbolism even though his doctorate was in mathematics.
Stanisław Leśniewski coined "mereology" in 1927, from the Greek word μέρος (méros, "part"), to refer to a formal theory of part-whole he devised in a series of highly technical papers published between 1916 and 1931, and translated in Leśniewski (1992). Leśniewski's student Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
, in his Appendix E to Woodger (1937) and the paper translated as Tarski (1984), greatly simplified Leśniewski's formalism. Other students (and students of students) of Lesniewski elaborated this "Polish mereology" over the course of the 20th century. For a good selection of the literature on Polish mereology, see Srzednicki and Rickey (1984). For a survey of Polish mereology, see Simons (1987). Since 1980 or so, however, research on Polish mereology has been almost entirely historical in nature.
A.N. Whitehead planned a fourth volume of Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
, on geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, but never wrote it. His 1914 correspondence with Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
reveals that his intended approach to geometry can be seen, with the benefit of hindsight, as mereological in essence. This work culminated in Whitehead (1916) and the mereological systems of Whitehead (1919, 1920).
In 1930, Henry Leonard completed a Harvard Ph.D. dissertation in philosophy, setting out a formal theory of the part-whole relation. This evolved into the "calculus of individuals" of Goodman and Leonard (1940). Goodman revised and elaborated this calculus in the three editions of Goodman (1951). The calculus of individuals is the starting point for the post-1970 revival of mereology among logicians, ontologists, and computer scientists, a revival well-surveyed in Simons (1987) and Casati and Varzi (1999).
Axioms and primitive notions
It is possible to formulate a "naive mereology" analogous to naive set theoryNaive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
. Doing so gives rise to paradoxes analogous to Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
. Let there be an object O such that every object that is not a proper part of itself is a proper part of O. Is O a proper part of itself? No, because no object is a proper part of itself; and yes, because it meets the specified requirement for inclusion as a proper part of O. (Every object is, of course, an improper part of itself. Another, though differently structured, paradox can be made using improper part instead of proper part; and another using improper or proper part.) Hence, mereology requires an axiomatic formulation.
A mereological "system" is a first-order theory
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
(with identity
Identity (philosophy)
In philosophy, identity, from , is the relation each thing bears just to itself. According to Leibniz's law two things sharing every attribute are not only similar, but are the same thing. The concept of sameness has given rise to the general concept of identity, as in personal identity and...
) whose universe of discourse consists of wholes and their respective parts, collectively called objects. Mereology is a collection of nested and non-nested axiomatic system
Axiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
s, not unlike the case with modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
.
The treatment, terminology, and hierarchical organization below follow Casati and Varzi (1999: Ch. 3) closely. For a more recent treatment, correcting certain misconceptions, see Hovda (2008). Lower-case letters denote variables ranging over objects. Following each symbolic axiom or definition is the number of the corresponding formula in Casati and Varzi, written in bold.
A mereological system requires at least one primitive binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
(dyadic
Dyadic
Dyadic may refer to:*Adicity of a mathematical relation or function *Dyadic communication* Dyadic counterpoint, the voice-against-voice conception of polyphony...
predicate). The most conventional choice for such a relation is Parthood (also called "inclusion"), "x is a part of y", written Pxy. Nearly all systems require that Parthood partially order the universe. The following defined relations, required for the axioms below, follow immediately from Parthood alone:
- An immediate defined predicate is "x is a proper part of y", written PPxy, which holds (i.e., is satisfiedContentment"Contentment" seems realistically defined as "enjoyment of whatever may be desired". That definition is realistic because the more contented an individual or community becomes the less extreme so more acceptable their desires will be...
, comes out true) if Pxy is true and Pyx is false. If Parthood is a partial order, ProperPart is a strict partial order.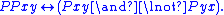 3.3
3.3
- An object lacking proper parts is an atom. The mereological universe consists of all objects we wish to think about, and all of their proper parts:
- Overlap: x and y overlap, written Oxy, if there exists an object z such that Pzx and Pzy both hold.
 3.1
3.1
- Overlap: x and y overlap, written Oxy, if there exists an object z such that Pzx and Pzy both hold.
- The parts of z, the "overlap" or "product" of x and y, are precisely those objects that are parts of both x and y.
- Underlap: x and y underlap, written Uxy, if there exists an object z such that x and y are both parts of z.
 3.2
3.2
- Underlap: x and y underlap, written Uxy, if there exists an object z such that x and y are both parts of z.
Overlap and Underlap are reflexive
Reflexive
Reflexive may refer to:In fiction:*MetafictionIn grammar:*Reflexive pronoun, a pronoun with a reflexive relationship with its self-identical antecedent*Reflexive verb, where a semantic agent and patient are the same...
, symmetric, and intransitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
.
Systems vary in what relations they take as primitive and as defined. For example, in extensional mereologies (defined below), Parthood can be defined from Overlap as follows:
 3.31
3.31The axioms are:
- Parthood partially orders the universeUniverseThe Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
:
- M1, ReflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
: An object is a part of itself. P.1
P.1 - M2, AntisymmetricAntisymmetric relationIn mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
: If Pxy and Pyx both hold, then x and y are the same object.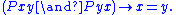 P.2
P.2 - M3, TransitiveTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
: If Pxy and Pyz, then Pxz.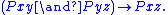 P.3
P.3
- M4, Weak Supplementation: If PPxy holds, there exists a z such that Pzy holds but Ozx does not.
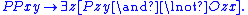 P.4
P.4
- M4, Weak Supplementation: If PPxy holds, there exists a z such that Pzy holds but Ozx does not.
- M5, Strong Supplementation: Replace "PPxy holds" in M4 with "Pyx does not hold".
 P.5
P.5
- M5', Atomistic Supplementation: If Pxy does not hold, then there exists an atom z such that Pzx holds but Ozy does not.
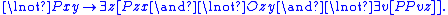 P.5'
P.5'
- Top: There exists a "universal object", designated W, such that PxW holds for any x.
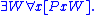 3.20
3.20
- Top is a theorem if M8 holds.
- Bottom: There exists an atomic "null object", designated N, such that PNx holds for any x.
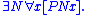 3.22
3.22
- M6, Sum: If Uxy holds, there exists a z, called the "sum" or "fusion" of x and y, such that the objects overlapping of z are just those objects that overlap either x or y.
 P.6
P.6 - M7, Product: If Oxy holds, there exists a z, called the "product" of x and y, such that the parts of z are just those objects that are parts of both x and y.
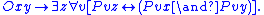 P.7
P.7
- If Oxy does not hold, x and y have no parts in common, and the product of x and y is undefined.
- M8, Unrestricted Fusion: Let φ(x) be a first-orderFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
formula in which x is a free variable. Then the fusion of all objects satisfying φ exists. P.8
P.8
- M8, Unrestricted Fusion: Let φ(x) be a first-order
- M8 is also called "General Sum Principle", "Unrestricted Mereological Composition", or "Universalism". M8 corresponds to the principle of unrestricted comprehension of naive set theoryNaive set theoryNaive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
, which gives rise to Russell's paradoxRussell's paradoxIn the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
. There is no mereological counterpart to this paradox simply because Parthood, unlike set membership, is reflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
.
- M8', Unique Fusion: The fusions whose existence M8 asserts are also unique. P.8'
- M9, Atomicity: All objects are either atoms or fusions of atoms.
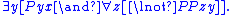 P.10
P.10
Various systems
Simons (1987), Casati and Varzi (1999) and Hovda (2008) describe many mereological systems whose axioms are taken from the above list. We adopt the boldface nomenclature of Casati and Varzi. The best-known such system is the one called classical extensional mereology, hereinafter abbreviated CEM (other abbreviations are explained below). In CEM, P.1 through P.8' hold as axioms or are theorems. M9, Top, and Bottom are optional.The systems in the table below are partially ordered by inclusion
Inclusion
Inclusion may refer to:- Metallurgy :*Inclusion , a type of metal casting defect*Inclusions in Aluminium Alloys, solid particles in liquid aluminium alloy- Social inclusion of persons :...
, in the sense that, if all the theorems of system A are also theorems of system B, but the converse is not necessarily true, then B includes A. The resulting Hasse diagram
Hasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
is similar to that in Fig. 2, and Fig. 3.2 in Casati and Varzi (1999: 48).
| Label | Name | System | Included Axioms |
|---|---|---|---|
| M1-M3 | Parthood is a partial order | M | M1–M3 |
| M4 | Weak Supplementation | MM | M, M4 |
| M5 | Strong Supplementation | EM | M, M5 |
| M5' | Atomistic Supplementation | ||
| M6 | General Sum Principle (Sum) | ||
| M7 | Product | CEM | EM, M6–M7 |
| M8 | Unrestricted Fusion | GM | M, M8 |
| GEM | EM, M8 | ||
| M8' | Unique Fusion | GEM | EM, M8' |
| M9 | Atomicity | AGEM | M2, M8, M9 |
| AGEM | M, M5', M8 |
There are two equivalent ways of asserting that the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
is partially ordered: Assume either M1–M3, or that Proper Parthood is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
and asymmetric
Asymmetric relation
Asymmetric often means, simply: not symmetric. In this sense an asymmetric relation is a binary relation which is not a symmetric relation.That is,\lnot....
, hence a strict partial order. Either axiomatization results in the system M. M2 rules out closed loops formed using Parthood, so that the part relation is well-founded. Sets are well-founded if the axiom of Regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
is assumed. The literature contains occasional philosophical and common-sense objections to the transitivity of Parthood.
M4 and M5 are two ways of asserting supplementation, the mereological analog of set complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
ation, with M5 being stronger because M4 is derivable from M5. M and M4 yield minimal mereology, MM. MM, reformulated in terms of Proper Part, is Simons's (1987) preferred minimal system.
In any system in which M5 or M5' are assumed or can be derived, then it can be proved that two objects having the same proper parts are identical. This property is known as Extensionality
Extensionality
In logic, extensionality, or extensional equality refers to principles that judge objects to be equal if they have the same external properties...
, a term borrowed from set theory, for which extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
is the defining axiom. Mereological systems in which Extensionality holds are termed extensional, a fact denoted by including the letter E in their symbolic names.
M6 asserts that any two underlapping objects have a unique sum; M7 asserts that any two overlapping objects have a unique product. If the universe is finite or if Top is assumed, then the universe is closed under sum. Universal closure of Product and of supplementation relative to W requires Bottom. W and N are, evidently, the mereological analog of the universal
Universal set
In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
and empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
s, and Sum and Product are, likewise, the analogs of set-theoretical union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
and intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
. If M6 and M7 are either assumed or derivable, the result is a mereology with closure.
Because Sum and Product are binary operations, M6 and M7 admit the sum and product of only a finite number of objects. The fusion axiom, M8, enables taking the sum of infinitely many objects. The same holds for Product, when defined. At this point, mereology often invokes set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, but any recourse to set theory is eliminable by replacing a formula with a quantified
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
variable ranging over a universe of sets by a schematic formula with one free variable. The formula comes out true (is satisfied) whenever the name of an object that would be a member of the set (if it existed) replaces the free variable. Hence any axiom with sets can be replaced by an axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
with monadic atomic subformulae. M8 and M8' are schemas of just this sort. The syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
of a first-order theory can describe only a denumerable number of sets; hence, only denumerably many sets may be eliminated in this fashion, but this limitation is not binding for the sort of mathematics contemplated here.
If M8 holds, then W exists for infinite universes. Hence, Top need be assumed only if the universe is infinite and M8 does not hold. It is interesting to note that Top (postulating W) is not controversial, but Bottom (postulating N) is. Leśniewski rejected Bottom, and most mereological systems follow his example (an exception is the work of Richard Milton Martin
Richard Milton Martin
Richard Milton Martin was an American logician and analytic philosopher. In his Ph.D. thesis written under Frederic Fitch, Martin discovered virtual sets a bit before Quine, and was possibly the first non-Pole other than Joseph Henry Woodger to employ a mereological system...
). Hence, while the universe is closed under sum, the product of objects that do not overlap is typically undefined. A system with W but not N is isomorphic to:
- A Boolean algebra lacking a 0
- A join semilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
bounded from above by 1. Binary fusion and W interpret join and 1, respectively.
Postulating N renders all possible products definable, but also transforms classical extensional mereology into a set-free model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of Boolean algebra.
If sets are admitted, M8 asserts the existence of the fusion of all members of any nonempty set. Any mereological system in which M8 holds is called general, and its name includes G. In any general mereology, M6 and M7 are provable. Adding M8 to an extensional mereology results in general extensional mereology, abbreviated GEM; moreover, the extensionality renders the fusion unique. On the converse, however, if the fusion asserted by M8 is assumed unique, so that M8' replaces M8, then - as Tarski (1929) had shown - M3 and M8' suffice to axiomatize GEM, a remarkably economical result. Simons (1987: 38–41) lists a number of GEM theorems.
M2 and a finite universe necessarily imply Atomicity, namely that everything either is an atom or includes atoms among its proper parts. If the universe is infinite, Atomicity requires M9. Adding M9 to any mereological system, X results in the atomistic variant thereof, denoted AX. Atomicity permits economies, for instance, assuming that M5' implies Atomicity and extensionality, and yields an alternative axiomatization of AGEM.
Set theory
Stanisław Leśniewski rejected set theory, a stance that has come to be known as nominalismNominalism
Nominalism is a metaphysical view in philosophy according to which general or abstract terms and predicates exist, while universals or abstract objects, which are sometimes thought to correspond to these terms, do not exist. Thus, there are at least two main versions of nominalism...
. For a long time, nearly all philosophers and mathematicians avoided mereology, seeing it as tantamount to a rejection of set theory. Goodman too was a nominalist, and his fellow nominalist Richard Milton Martin
Richard Milton Martin
Richard Milton Martin was an American logician and analytic philosopher. In his Ph.D. thesis written under Frederic Fitch, Martin discovered virtual sets a bit before Quine, and was possibly the first non-Pole other than Joseph Henry Woodger to employ a mereological system...
employed a version of the calculus of individuals throughout his career, starting in 1941.
Much early work on mereology was motivated by a suspicion that set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
was ontologically
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
suspect, and that Occam's Razor
Occam's razor
Occam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
requires that one minimise the number of posits in one's theory of the world and of mathematics. Mereology replaces talk of "sets" of objects with talk of "sums" of objects, objects being no more than the various things that make up wholes.
Many logicians and philosophers reject these motivations, on such grounds as:
- They deny that sets are in any way ontologically suspect
- Occam's RazorOccam's razorOccam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
, when applied to abstract objectAbstract objectAn abstract object is an object which does not exist at any particular time or place, but rather exists as a type of thing . In philosophy, an important distinction is whether an object is considered abstract or concrete. Abstract objects are sometimes called abstracta An abstract object is an...
s like sets, is either a dubious principle or simply false - Mereology itself is guilty of proliferating new and ontologically suspect entities such as fusions.
For a survey of attempts to found mathematics without using set theory, see Burgess and Rosen (1997).
In the 1970s, thanks in part to Eberle (1970), it gradually came to be understood that one can employ mereology regardless of one's ontological stance regarding sets. This understanding is called the "ontological innocence" of mereology. This innocence stems from the mereology being formalizable in either of two equivalent ways:
- Quantified variables ranging over a universeUniverseThe Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
of sets - Schematic predicates with a single free variable.
Once it became clear that mereology is not tantamount to a denial of set theory, mereology became largely accepted as a useful tool for formal ontology
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
and metaphysics
Metaphysics
Metaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
.
In set theory, singletons are "atoms" that have no (non-empty) proper parts; many consider set theory useless or incoherent (not "well-founded") if sets cannot be built up from unit sets. The calculus of individuals was thought to require that an object either have no proper parts, in which case it is an "atom", or be the mereological sum of atoms. Eberle (1970) showed how to construct a calculus of individuals lacking "atoms
Atomism
Atomism is a natural philosophy that developed in several ancient traditions. The atomists theorized that the natural world consists of two fundamental parts: indivisible atoms and empty void.According to Aristotle, atoms are indestructible and immutable and there are an infinite variety of shapes...
", i.e., one where every object has a "proper part" (defined below) so that the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
is infinite.
There are analogies between the axioms of mereology and those of standard Zermelo-Fraenkel set theory (ZF), if Parthood is taken as analogous to subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
in set theory. On the relation of mereology and ZF, also see Bunt (1985). One of the very few contemporary set theorist to discuss mereology is Potter (2004).
Lewis (1991) went further, showing informally that mereology, augmented by a few ontological
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
assumptions and plural quantification
Plural quantification
In mathematics and logic, plural quantification is the theory that an individual variable x may take on plural, as well as singular values. As well as substituting individual objects such as Alice, the number 1, the tallest building in London etc...
, and some novel reasoning about singletons, yields a system in which a given individual can be both a member and a subset of another individual. In the resulting system, the axioms of ZFC (and of Peano arithmetic) are theorems.
Forrest (2002) revises Lewis's analysis by first formulating a generalization of CEM, called "Heyting mereology", whose sole nonlogical primitive is Proper Part, assumed transitive and antireflexive. There exists a "fictitious" null individual that is a proper part of every individual. Two schemas assert that every lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
join exists (lattices are complete
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
) and that meet distributes over join. On this Heyting mereology, Forrest erects a theory of pseudosets, adequate for all purposes to which sets have been put.
Mathematics
Husserl never claimed that mathematics could or should be grounded in part-whole rather than set theory. Lesniewski consciously derived his mereology as an alternative to set theory as a foundation of mathematics, but did not work out the details. Goodman and Quine (1947) tried to develop the natural and real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s using the calculus of individuals, but were mostly unsuccessful; Quine did not reprint that article in his Selected Logic Papers. In a series of chapters in the books he published in the last decade of his life, Richard Milton Martin
Richard Milton Martin
Richard Milton Martin was an American logician and analytic philosopher. In his Ph.D. thesis written under Frederic Fitch, Martin discovered virtual sets a bit before Quine, and was possibly the first non-Pole other than Joseph Henry Woodger to employ a mereological system...
set out to do what Goodman and Quine had abandoned 30 years prior. A recurring problem with attempts to ground mathematics in mereology is how to build up the theory of relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
while abstaining from set-theoretic definitions of the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
. Martin argued that Eberle's (1970) theory of relational individuals solved this problem.
To date, the only persons well trained in mathematics to write on mereology have been Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
and Rolf Eberle. Eberle (1970) clarified the relation between mereology and Boolean algebra, and mereology and set theory. He is one of the very few contributors to mereology to prove sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
and complete each system he describes.
Topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
notions of boundaries
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
and connection can be married to mereology, resulting in mereotopology
Mereotopology
In formal ontology, a branch of metaphysics, and in ontological computer science, mereotopology is a first-order theory, embodying mereological and topological concepts, of the relations among wholes, parts, parts of parts, and the boundaries between parts....
; see Casati and Varzi (1999: chpts. 4,5). Whitehead's 1929 Process and Reality
Process and Reality
In philosophy, especially metaphysics, the book Process and Reality by Alfred North Whitehead sets out its author's philosophy of organism, also called process philosophy...
contains a good deal of informal mereotopology
Mereotopology
In formal ontology, a branch of metaphysics, and in ontological computer science, mereotopology is a first-order theory, embodying mereological and topological concepts, of the relations among wholes, parts, parts of parts, and the boundaries between parts....
.
Mereology and natural language
Bunt (1985), a study of the semanticsSemantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
of natural language, shows how mereology can help understand such phenomena as the mass–count distinction
Mass noun
In linguistics, a mass noun is a noun that refers to some entity as an undifferentiated unit rather than as something with discrete subsets. Non-count nouns are best identified by their syntactic properties, and especially in contrast with count nouns. The semantics of mass nouns are highly...
and verb aspect
Grammatical aspect
In linguistics, the grammatical aspect of a verb is a grammatical category that defines the temporal flow in a given action, event, or state, from the point of view of the speaker...
. But Nicolas (2008) argues that a different logical framework, called plural logic
Plural quantification
In mathematics and logic, plural quantification is the theory that an individual variable x may take on plural, as well as singular values. As well as substituting individual objects such as Alice, the number 1, the tallest building in London etc...
, should be used for that purpose.
Also, natural language
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
often employs "part of" in ambiguous ways (Simons 1987 discusses this at length). Hence, it is unclear how, if at all, one can translate certain natural language expressions into mereological predicates. Steering clear of such difficulties may require limiting the interpretation of mereology to mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and natural science
Natural science
The natural sciences are branches of science that seek to elucidate the rules that govern the natural world by using empirical and scientific methods...
. Casati and Varzi (1999), for example, limit the scope of mereology to physical objects.
Important surveys
The books Simons (1987) and Casati and Varzi (1999) differ in their strengths:- Simons (1987) sees mereology primarily as a way of formalizing ontologyOntologyOntology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
and metaphysicsMetaphysicsMetaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
. His strengths include the connections between mereology and:- The work of Stanislaw LeśniewskiStanislaw LesniewskiStanisław Leśniewski was a Polish mathematician, philosopher and logician.Leśniewski went to a high school in Irkutsk...
and his descendants - Various continental philosophers, especially Edmund HusserlEdmund HusserlEdmund Gustav Albrecht Husserl was a philosopher and mathematician and the founder of the 20th century philosophical school of phenomenology. He broke with the positivist orientation of the science and philosophy of his day, yet he elaborated critiques of historicism and of psychologism in logic...
- Contemporary English-speaking technical philosophers such as Kit FineKit FineKit Fine is Silver Professor of Philosophy and Mathematics at New York University. He previously taught for several years at UCLA...
and Roderick ChisholmRoderick ChisholmRoderick M. Chisholm was an American philosopher known for his work on epistemology, metaphysics, free will, and the philosophy of perception. He received his Ph.D. at Harvard University under Clarence Irving Lewis and Donald C. Williams, and taught at Brown University... - Recent work on formal ontologyFormal ontologyIn philosophy, the term formal ontology is used to refer to an ontology defined by axioms in a formal language with the goal to provide an unbiased view on reality, which can help the modeler of domain- or application-specific ontologies to avoid possibly erroneous ontological assumptions...
and metaphysicsMetaphysicsMetaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
, including continuants, occurrents, class nouns, mass nounMass nounIn linguistics, a mass noun is a noun that refers to some entity as an undifferentiated unit rather than as something with discrete subsets. Non-count nouns are best identified by their syntactic properties, and especially in contrast with count nouns. The semantics of mass nouns are highly...
s, and ontological dependence and integrityIntegrityIntegrity is a concept of consistency of actions, values, methods, measures, principles, expectations, and outcomes. In ethics, integrity is regarded as the honesty and truthfulness or accuracy of one's actions... - Free logicFree logicA free logic is a logic with fewer existential presuppositions than classical logic. Free logics may allow for terms that do not denote any object. Free logics may also allow models that have an empty domain...
as a background logic - Extending mereology with tense logic and modal logicModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
- Boolean algebras and lattice theory.
- The work of Stanislaw Leśniewski
- Casati and Varzi (1999) see mereology primarily as a way of understanding the material world and how humans interact with it. Their strengths include the connections between mereology and:
- A "proto-geometry" for physical objects
- TopologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and mereotopologyMereotopologyIn formal ontology, a branch of metaphysics, and in ontological computer science, mereotopology is a first-order theory, embodying mereological and topological concepts, of the relations among wholes, parts, parts of parts, and the boundaries between parts....
, especially boundariesBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
, regions, and holes - A formal theory of events
- Theoretical computer scienceComputer scienceComputer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
- The writings of Alfred North WhiteheadAlfred North WhiteheadAlfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
, especially his Process and RealityProcess and RealityIn philosophy, especially metaphysics, the book Process and Reality by Alfred North Whitehead sets out its author's philosophy of organism, also called process philosophy...
and work descended therefrom.
Simons devotes considerable effort to elucidating historical notations. The notation of Casati and Varzi is often used. Both books include excellent bibliographies.
To these works should be added Hovda (2008), which presents the latest state of the art on the axiomatization of mereology.
See also
- Attitude polarizationAttitude polarizationAttitude polarization, also known as belief polarization, is a phenomenon in which a disagreement becomes more extreme as the different parties consider evidence on the issue. It is one of the effects of confirmation bias: the tendency of people to search for and interpret evidence selectively, to...
- Gunk (mereology)Gunk (mereology)In mereology, an area of philosophical logic, the term gunk applies to any whole whose parts all have further proper parts. That is, a gunky object is not made of indivisible atoms. In contrast, an atomic individual is entirely decomposable into atoms.If point-sized objects are always simple, then...
- Implicate and explicate order according to David BohmImplicate and explicate order according to David BohmAccording to David Bohm's theory, implicate and explicate orders are characterised by:-David Bohm's challenges to some generally prevailing views:...
- Mereological essentialismMereological essentialismMereological essentialism is a philosophical thesis about the relationship between wholes and its parts, and the conditions for their persistence...
- Mereological nihilismMereological nihilismMereological nihilism is the position that objects with proper parts do not exist , and only basic building blocks without parts exist...
- MereotopologyMereotopologyIn formal ontology, a branch of metaphysics, and in ontological computer science, mereotopology is a first-order theory, embodying mereological and topological concepts, of the relations among wholes, parts, parts of parts, and the boundaries between parts....
- Monad (Greek philosophy)Monad (Greek philosophy)Monad , according to the Pythagoreans, was a term for Divinity or the first being, or the totality of all beings, Monad being the source or the One meaning without division....
- Plural quantificationPlural quantificationIn mathematics and logic, plural quantification is the theory that an individual variable x may take on plural, as well as singular values. As well as substituting individual objects such as Alice, the number 1, the tallest building in London etc...
- Simple (philosophy)
- Whitehead's point-free geometryWhitehead's point-free geometryIn mathematics, point-free geometry is a geometry whose primitive ontological notion is region rather than point. Two axiomatic systems are set out below, one grounded in mereology, the other in mereotopology and known as connection theory...
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
:- "Mereology" – Achille Varzi.
- "Boundary" – Achille Varzi.
- Synergy and Dysergy in Mereologic Geometries"http://www.wikinfo.org/index.php/Synergy_and_Dysergy_in_Mereologic_Geometries" - Albert Carpenter

