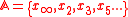P-adic quantum mechanics
Encyclopedia
P-adic quantum mechanics is a relatively recent approach to understanding the nature of fundamental physics. It is the application of p-adic analysis
to quantum mechanics
. The p-adic number
s are a counterintuitive arithmetic system that was discovered by the German mathematician Kurt Hensel
in about 1899. The closely related Adeles
and Ideles were introduced in the 1930s by André Weil
. Their study has now transformed into a major branch of mathematics. They were occasionally applied to the physical sciences, but it wasn't until a publication by the Russian mathematician Volovich in 1987 that the subject was taken seriously. There are now hundreds of research articles on the subject, along with international journals as well.
This article provides an introduction to the subject, followed by a review of the mathematical concepts involved. It then considers modern research on the subject, from Schrodinger-like equations to more exploratory ideas. Finally it lists some precise examples that have been considered.
formalism of nanotechnology
presents a formidable challenge. Most researchers feel that the geometry and topology of the sub-Planck lengths need not have any relation whatever to ordinary geometry and topology. Instead the latter are believed to emerge
from the former, just as the color of flowers emerges from atoms. Currently many frameworks have been proposed, and p-adic analysis is a reasonable candidate, having several accomplishments in its favor.
Another motivation for applying p-adic analysis to science is that the divergences that plague quantum field theory
remain problematic as well. It is felt that by exploring different approaches, such inelegant techniques as renormalization
might become unnecessary. Another consideration is that since no primes have any special status in p-adic analysis, it might be more natural and instructive to work with adeles.
There are two main approaches to the subject. The first considers particles in a p-adic potential well, and the goal is to find solutions with smoothly varying complex-valued wavefunctions. Here the solutions to have a certain amount of familiarity from ordinary life. The second considers particles in p-adic potential wells, and the goal is to find p-adic valued wavefunctions. In this case, the physical interpretation is more difficult. Yet the math often exhibits striking characteristics, therefore people continue to explore it. The situation was summed up in 2005 by one scientist as follows: "I simply cannot think of all this as a sequence of amusing accidents and dismiss it as a 'toy model'. I think more work on this is both needed and worthwhile."Peter G.O. Freund, p-adic Strings and their Applications, http://arxiv.org/abs/hep-th/0510192
, but are often regarded as a curiousity. It turns out that they have major significance. The reason they work is that they are a subset of the p-adic integers. Ostrowski's theorem
states that there are essentially only two completions
of the rational number
s, depending on the metric
considered: these are the real number
s and the p-adic numbers. One completes the rationals by adding the limit of all Cauchy sequence
s to the set. The completions are different because of the two different ways of measuring distance.The two spaces are complete as a metric space, but neither are algebraically complete. That requires generalizing to an infinite-dimensional space. The former obey a triangle inequality of the form |x+y| ≤ |x| + |y|, but the latter obey the stronger form of |x+y| ≤ max{|x|, |y|}; this is sometimes called an ultrametric space. In summary, there exist two different types of algebraic systems.
There is a question of how to unify these two foundational ideas, as they behave very differently in both space and time. This is solved by considering the patterns that occur, when one welds them together into a single mathematical object. This is the ring of adeles
. It is of the form
where
is a real number, and the 
are in 
. The infinity sign in 
stands for the "prime at infinity". So an adele ring is essentially a direct product
. The idele group is defined as the essentially invertible elements:
Many familiar structures carry over to the adeles. For example, trigonometric functions, ex and log (x) have been constructed, as well as special functions like the Riemann zeta function, along with integral transforms like the Mellin
and Fourier transform
. This ring has many interesting properties. For instance, quadratic polynomials obey the Hasse local-global principle: a rational number is the solution of a quadratic polynomial equation if and only is it has a solution in R and Qp for all primes p. In addition, the real and p-adic norms are related to each other by the remarkable adelic product formula:
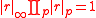
where is a nonzero rational number. For example, one might consider the number 12. In this case, r2 = 0011, r3 = 011, r5 = 22, r7 = 51 and r11 = 11. So |r2| = 1/4, |r3| = 1/3, |r5| = 1, |r7| = 1, |r11| = 1, and all the rest are ones. Hence, 12*1/4*1/3*1*1*1*1*1*1*1 = 1. In string theory
, a similar product formula holds not only at the tree level, but generalization to full amplitudes has also been proposed. This is covered in more detail later in the article.
Many upper-division science students are familiar with the particle in a box
, or the particle in a ring
. But there are also other types of potential wells. For instance, one may also consider the fractal
potential wells. The solution of Schrodinger-like equations
for potentials of this kind has been of interest for some time. Not only is it challenging to solve for puzzles like this, but it can be used for approximating complicated potentials as well, such as those that arise in the design of microchip
s. For example, one group of authors study the Schrödinger equation as it applies to a self-similar potential. Another group studied the potentials constructed from the Riemann zeros and prime number sequences. They estimate the fractal dimension
to be D = 1.5 for the Riemann zeros, and D = 1.8 for the prime numbers.
The question of what happens when waves interact with fractal structures has been studied by many researchers. The p-adic numbers are an excellent method for constructing fractal potential wells. For instance, one might consider a Dirac potential. This is simply a flat plane that contains a negative-valued Dirac delta function
. One can think of this as a positive integer surrounded by zeros, and each of those surrounded by zeros, and each of those surrounded by zeros, and so on. As another example, one may think of a number surrounded by half its value, and each of those numbers by half their value, and so on. In this case it is more interesting, because half of 3 mod 7 is 5; therefore it seems to be bigger.
Path integrals
As early as 1965, Feynman had stated that path integrals have fractal-like properties. And, as there does not exist a suitable p-adic Schrodinger equation, path integrals are employed instead. One author states that "Feynman's adelic path integral is a fundamental object in mathematical physics of quantum phenomena". In order to do computations, certain details have to be made precise. For instance, one may define a meaningful derivative operator. In addition, both A and A* have a translation-invariant Haar measure
:
This allows one to compute integrals. For the sum over histories, Gaussian integral
s are vital. It turns out that Gaussian integrals satisfy a generalization of the adelic product formula introduced before, namely:
where
is an additive character from the adeles to C given by
and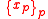
is the fractional part of 
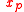in the ordinary p-adic expression for x. This can be thought of as a strong generalization of the homomorphism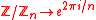
Now the adelic path integral, with input parameters in A and generating complex-valued wavefunctions is
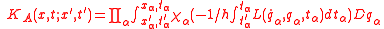
and similar to the case for real parameters, the eigenvalue problem is
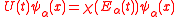
where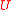
is the time-development operator, 
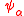are adelic eigenfunctions, and 
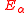is the adelic energy. Here the notation has been simplified by using the subscript 
, which stands for all primes including the prime at infinity. One notices the additive character 
which allows these to be complex-valued integrals. The path integral can be generalized to p-adic time as well.
Lorentz group
The p-adic generalization of the Lorentz group
has been considered. In 2008, an article was published on the group, in fields over primes congruent to 7 mod 8. The author finds dense subsets of the group over the rationals, maps them to the group over the p-adic numbers, and finally to the group over the integers mod a prime. In this way, arbitrarily dense subsets of the group can be found.
Finite fields
The research has not been limited to the inverse limit
of the integers mod a prime number, because all finite field
s have similar constructions. In fact, every finite field is the quotient of an ideal of that inverse limit, and therefore the system is actually a tower of ideals. The study of quantum mechanics in finite fields has been considered by a number of authors. One motivation is that if spacetime is discrete, then perhaps continuous spacetime can be viewed as an approximation to finite fields. The theory of supersymmetry has been studied in finite fields as well.
Riemann zeta function
It can be shown that ground state of adelic quantum harmonic oscillator is
where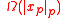
is 1 if 
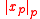is a p-adic integer, and 0 otherwise. One notices the close similarity to the ordinary complex-valued ground state. Applying the adelic version of the Mellin transform, we have
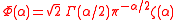
where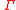
is the gamma function
, and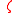
is the Riemann zeta function. Now there is a famous functional equation
called the Tate formula, which says that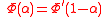
Here the left hand side is the Mellin transform, and the right hand side is the Mellin transform of the Fourier transform. But just as in the ordinary case, the Fourier transform does not change the result. So one can apply this formula to the previous one, and we arrive at the famous functional relation for the Riemann zeta function:
"It is remarkable that such simple physical system as harmonic oscillator is related to so significant mathematical object as the Reimann zeta function". In addition, the statistical mechanics partition function
for the free Riemann gasThis is not a real gas, but rather a fictitious one. One might think of the famous experiment of heating up hydrogen gas, and viewing the spectral lines. In the same way, heating up the free Riemann gas would allow one to view (the differences of) a series based on the prime numbers. is given by the Riemann zeta function:
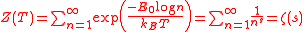
Veneziano amplitude
Another application involves the adelic product formula in a different way. In string theory, one computes crossing symmetric Veneziano amplitude
s. The amplitude A (a, b) describes the scattering of four tachyons in the 26-dimensional open bosonic string. These amplitudes are not easy to compute. However, in 1987 an adelic product formula for this was discovered; it is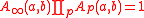
This allows the four-point amplitudes, and all higher amplitudes to be computed at the tree level exactly, as the inverse of the much simpler p-adic amplitudes. This discovery has generated a quite a bit of activity in string theory. The situation is not as easy for the closed bosonic string, but studies are still being pursued.
Representation theory
P-adic representation theory
has been extensively studied. One group of authors studies the structure of elementary particles, by means of the projective representation
s of the p-adic Poincare group
. This a generalization of the famous theorem of Wigner, who showed that all projective unitary representation
s of the poincare group lift to unitary representations of its (universal) double cover. They show that the p-adic version of massive particles cannot have conformal symmetry
, by studying the embedding of the p-adic poincare group into the p-adic conformal spacetime. Another group studied p-adic symplectic theory; more specifically, the representations of GL(2n) over a p-adic field that admit an invariant under the symplectic group. Yet another has studied "extrametaplectic" representations.
Principal bundles
The math associated with this study is elegantly formulated in the language of gauge theory
. In particular, one studies the wavefunctions in a tangent space known as a principal bundle
. This helps to formulate a self-consistent theory. In this case, there is an idele-group bundle. It can be matrix-valued, in which case it may be noncommutative as well.
Quantum cosmology
The theory has also been applied to quantum cosmology. One group of authors study the relevance of "quantum rolling tachyons and corresponding inflation scenario" in terms of adelic quantum cosmology.
Percolation theory
is used by many to study the behaviour of integrated circuits and other designs. This is because the materials are so small that they qualify for disordered materials theory. Many disordered materials "exhibit geometrical inhomogeneties over a broad range of length scales". More importantly, near the percolation threshold, the geometry is fractal. This is well known from the theory of phase transitions. In 2011, one group studied potential theory on the Sierpinski gasket. They develop a mathematical formalism, and show how it can be used to develop a potential theory on this space, even though it is technically not a manifold. Another group studied Josephson junction arrays of periodically repeated Sierpinski gaskets.
.
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s are a counterintuitive arithmetic system that was discovered by the German mathematician Kurt Hensel
Kurt Hensel
Kurt Wilhelm Sebastian Hensel was a German mathematician born in Königsberg, Prussia.He was the son of the landowner and entrepreneur Sebastian Hensel, brother of the philosopher Paul Hensel, grandson of the composer Fanny Mendelssohn and the painter Wilhelm Hensel, and a descendant of the...
in about 1899. The closely related Adeles
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
and Ideles were introduced in the 1930s by André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
. Their study has now transformed into a major branch of mathematics. They were occasionally applied to the physical sciences, but it wasn't until a publication by the Russian mathematician Volovich in 1987 that the subject was taken seriously. There are now hundreds of research articles on the subject, along with international journals as well.
This article provides an introduction to the subject, followed by a review of the mathematical concepts involved. It then considers modern research on the subject, from Schrodinger-like equations to more exploratory ideas. Finally it lists some precise examples that have been considered.
Introduction
Many studies of nature deal with questions that occur at the Planck length, in which ordinary reality doesn't seem to exist. In some ways, the experimental apparatus and experimenter become indistinguishable, so that no experiments can be done. The unification of the immensity of cosmology with the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
formalism of nanotechnology
Nanotechnology
Nanotechnology is the study of manipulating matter on an atomic and molecular scale. Generally, nanotechnology deals with developing materials, devices, or other structures possessing at least one dimension sized from 1 to 100 nanometres...
presents a formidable challenge. Most researchers feel that the geometry and topology of the sub-Planck lengths need not have any relation whatever to ordinary geometry and topology. Instead the latter are believed to emerge
Emergence
In philosophy, systems theory, science, and art, emergence is the way complex systems and patterns arise out of a multiplicity of relatively simple interactions. Emergence is central to the theories of integrative levels and of complex systems....
from the former, just as the color of flowers emerges from atoms. Currently many frameworks have been proposed, and p-adic analysis is a reasonable candidate, having several accomplishments in its favor.
Another motivation for applying p-adic analysis to science is that the divergences that plague quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
remain problematic as well. It is felt that by exploring different approaches, such inelegant techniques as renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
might become unnecessary. Another consideration is that since no primes have any special status in p-adic analysis, it might be more natural and instructive to work with adeles.
There are two main approaches to the subject. The first considers particles in a p-adic potential well, and the goal is to find solutions with smoothly varying complex-valued wavefunctions. Here the solutions to have a certain amount of familiarity from ordinary life. The second considers particles in p-adic potential wells, and the goal is to find p-adic valued wavefunctions. In this case, the physical interpretation is more difficult. Yet the math often exhibits striking characteristics, therefore people continue to explore it. The situation was summed up in 2005 by one scientist as follows: "I simply cannot think of all this as a sequence of amusing accidents and dismiss it as a 'toy model'. I think more work on this is both needed and worthwhile."Peter G.O. Freund, p-adic Strings and their Applications, http://arxiv.org/abs/hep-th/0510192
Review of p-adic and adelic analysis
The ordinary real numbers are familiar to everyone. Still reasonably familiar, but less so, are the integers mod n. They are sometimes studied in courses on number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, but are often regarded as a curiousity. It turns out that they have major significance. The reason they work is that they are a subset of the p-adic integers. Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
states that there are essentially only two completions
Completion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
of the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, depending on the metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
considered: these are the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and the p-adic numbers. One completes the rationals by adding the limit of all Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s to the set. The completions are different because of the two different ways of measuring distance.The two spaces are complete as a metric space, but neither are algebraically complete. That requires generalizing to an infinite-dimensional space. The former obey a triangle inequality of the form |x+y| ≤ |x| + |y|, but the latter obey the stronger form of |x+y| ≤ max{|x|, |y|}; this is sometimes called an ultrametric space. In summary, there exist two different types of algebraic systems.
There is a question of how to unify these two foundational ideas, as they behave very differently in both space and time. This is solved by considering the patterns that occur, when one welds them together into a single mathematical object. This is the ring of adeles
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
. It is of the form
where
is a real number, and the are in . The infinity sign in stands for the "prime at infinity". So an adele ring is essentially a direct productDirect product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
. The idele group is defined as the essentially invertible elements:
Many familiar structures carry over to the adeles. For example, trigonometric functions, ex and log (x) have been constructed, as well as special functions like the Riemann zeta function, along with integral transforms like the Mellin
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
and Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. This ring has many interesting properties. For instance, quadratic polynomials obey the Hasse local-global principle: a rational number is the solution of a quadratic polynomial equation if and only is it has a solution in R and Qp for all primes p. In addition, the real and p-adic norms are related to each other by the remarkable adelic product formula:
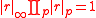
where is a nonzero rational number. For example, one might consider the number 12. In this case, r2 = 0011, r3 = 011, r5 = 22, r7 = 51 and r11 = 11. So |r2| = 1/4, |r3| = 1/3, |r5| = 1, |r7| = 1, |r11| = 1, and all the rest are ones. Hence, 12*1/4*1/3*1*1*1*1*1*1*1 = 1. In string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, a similar product formula holds not only at the tree level, but generalization to full amplitudes has also been proposed. This is covered in more detail later in the article.
The research
Fractal potential wellsMany upper-division science students are familiar with the particle in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
, or the particle in a ring
Particle in a ring
In quantum mechanics, the case of a particle in a one-dimensional ring is similar to the particle in a box. The Schrödinger equation for a free particle which is restricted to a ring is...
. But there are also other types of potential wells. For instance, one may also consider the fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
potential wells. The solution of Schrodinger-like equations
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for potentials of this kind has been of interest for some time. Not only is it challenging to solve for puzzles like this, but it can be used for approximating complicated potentials as well, such as those that arise in the design of microchip
Microchip
Microchip can also refer to:* Integrated circuit, a set of electronic components on a single unit.* Microchip Technology, a company that makes popular 8, 16 and 32-bit microcontroller lines.* Microchip implant , a microchip implanted into animals....
s. For example, one group of authors study the Schrödinger equation as it applies to a self-similar potential. Another group studied the potentials constructed from the Riemann zeros and prime number sequences. They estimate the fractal dimension
Fractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
to be D = 1.5 for the Riemann zeros, and D = 1.8 for the prime numbers.
The question of what happens when waves interact with fractal structures has been studied by many researchers. The p-adic numbers are an excellent method for constructing fractal potential wells. For instance, one might consider a Dirac potential. This is simply a flat plane that contains a negative-valued Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. One can think of this as a positive integer surrounded by zeros, and each of those surrounded by zeros, and each of those surrounded by zeros, and so on. As another example, one may think of a number surrounded by half its value, and each of those numbers by half their value, and so on. In this case it is more interesting, because half of 3 mod 7 is 5; therefore it seems to be bigger.
Path integrals
As early as 1965, Feynman had stated that path integrals have fractal-like properties. And, as there does not exist a suitable p-adic Schrodinger equation, path integrals are employed instead. One author states that "Feynman's adelic path integral is a fundamental object in mathematical physics of quantum phenomena". In order to do computations, certain details have to be made precise. For instance, one may define a meaningful derivative operator. In addition, both A and A* have a translation-invariant Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
:
This allows one to compute integrals. For the sum over histories, Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
s are vital. It turns out that Gaussian integrals satisfy a generalization of the adelic product formula introduced before, namely:
where
is an additive character from the adeles to C given byand
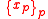is the fractional part of 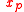in the ordinary p-adic expression for x. This can be thought of as a strong generalization of the homomorphism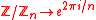Now the adelic path integral, with input parameters in A and generating complex-valued wavefunctions is
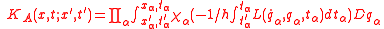
and similar to the case for real parameters, the eigenvalue problem is
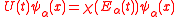
where
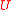is the time-development operator, 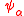are adelic eigenfunctions, and 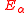is the adelic energy. Here the notation has been simplified by using the subscript , which stands for all primes including the prime at infinity. One notices the additive character which allows these to be complex-valued integrals. The path integral can be generalized to p-adic time as well.Lorentz group
The p-adic generalization of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
has been considered. In 2008, an article was published on the group, in fields over primes congruent to 7 mod 8. The author finds dense subsets of the group over the rationals, maps them to the group over the p-adic numbers, and finally to the group over the integers mod a prime. In this way, arbitrarily dense subsets of the group can be found.
Finite fields
The research has not been limited to the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the integers mod a prime number, because all finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s have similar constructions. In fact, every finite field is the quotient of an ideal of that inverse limit, and therefore the system is actually a tower of ideals. The study of quantum mechanics in finite fields has been considered by a number of authors. One motivation is that if spacetime is discrete, then perhaps continuous spacetime can be viewed as an approximation to finite fields. The theory of supersymmetry has been studied in finite fields as well.
Riemann zeta function
It can be shown that ground state of adelic quantum harmonic oscillator is
where
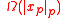is 1 if 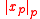is a p-adic integer, and 0 otherwise. One notices the close similarity to the ordinary complex-valued ground state. Applying the adelic version of the Mellin transform, we have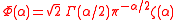where
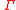is the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, and
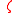is the Riemann zeta function. Now there is a famous functional equationFunctional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
called the Tate formula, which says that
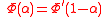
Here the left hand side is the Mellin transform, and the right hand side is the Mellin transform of the Fourier transform. But just as in the ordinary case, the Fourier transform does not change the result. So one can apply this formula to the previous one, and we arrive at the famous functional relation for the Riemann zeta function:
"It is remarkable that such simple physical system as harmonic oscillator is related to so significant mathematical object as the Reimann zeta function". In addition, the statistical mechanics partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
for the free Riemann gasThis is not a real gas, but rather a fictitious one. One might think of the famous experiment of heating up hydrogen gas, and viewing the spectral lines. In the same way, heating up the free Riemann gas would allow one to view (the differences of) a series based on the prime numbers. is given by the Riemann zeta function:
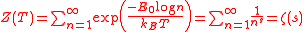
Veneziano amplitude
Another application involves the adelic product formula in a different way. In string theory, one computes crossing symmetric Veneziano amplitude
Veneziano amplitude
In theoretical physics, the Veneziano amplitude refers to the discovery made in 1968 by Italian theoretical physicist Gabriele Veneziano that the Euler beta function, when interpreted as a scattering amplitude, has many of the features needed to explain the physical properties of strongly...
s. The amplitude A (a, b) describes the scattering of four tachyons in the 26-dimensional open bosonic string. These amplitudes are not easy to compute. However, in 1987 an adelic product formula for this was discovered; it is
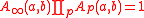
This allows the four-point amplitudes, and all higher amplitudes to be computed at the tree level exactly, as the inverse of the much simpler p-adic amplitudes. This discovery has generated a quite a bit of activity in string theory. The situation is not as easy for the closed bosonic string, but studies are still being pursued.
Representation theory
P-adic representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
has been extensively studied. One group of authors studies the structure of elementary particles, by means of the projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of the p-adic Poincare group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
. This a generalization of the famous theorem of Wigner, who showed that all projective unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of the poincare group lift to unitary representations of its (universal) double cover. They show that the p-adic version of massive particles cannot have conformal symmetry
Conformal symmetry
In theoretical physics, conformal symmetry is a symmetry under dilatation and under the special conformal transformations...
, by studying the embedding of the p-adic poincare group into the p-adic conformal spacetime. Another group studied p-adic symplectic theory; more specifically, the representations of GL(2n) over a p-adic field that admit an invariant under the symplectic group. Yet another has studied "extrametaplectic" representations.
Principal bundles
The math associated with this study is elegantly formulated in the language of gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
. In particular, one studies the wavefunctions in a tangent space known as a principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
. This helps to formulate a self-consistent theory. In this case, there is an idele-group bundle. It can be matrix-valued, in which case it may be noncommutative as well.
Quantum cosmology
The theory has also been applied to quantum cosmology. One group of authors study the relevance of "quantum rolling tachyons and corresponding inflation scenario" in terms of adelic quantum cosmology.
Examples
This section presents concrete examples of fractal or adelic systems which have been studied.One dimensional systems
The following one dimensional systems have been studied by means of the path integral formulation: the free particle, the particle in a constant field, the harmonic oscillator, and others as well.Particle on a Sierpinski gasket
Percolation theory
In mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation.-Introduction:...
is used by many to study the behaviour of integrated circuits and other designs. This is because the materials are so small that they qualify for disordered materials theory. Many disordered materials "exhibit geometrical inhomogeneties over a broad range of length scales". More importantly, near the percolation threshold, the geometry is fractal. This is well known from the theory of phase transitions. In 2011, one group studied potential theory on the Sierpinski gasket. They develop a mathematical formalism, and show how it can be used to develop a potential theory on this space, even though it is technically not a manifold. Another group studied Josephson junction arrays of periodically repeated Sierpinski gaskets.
Particle on a Cantor set
One group numerically solve a rescaled version of the Schrodinger equation for a particle in a Cantor-like potentialCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
.