Poker probability (Texas hold 'em)
Encyclopedia
In poker
, the probability of many events
can be determined by direct calculation. This article discusses computing probabilities for many commonly occurring events in the game of Texas hold 'em
and provides some probabilities
and odds
for specific situations. In most cases, the probabilities and odds are approximation
s due to rounding
.
When calculating probabilities for a card game such as Texas Hold 'em, there are two basic approaches. The first approach is to determine the number of outcomes that satisfy the condition being evaluated and divide this by the total number of possible outcomes.
For example, there are six outcomes (ignoring order) for being dealt a pair of aces in Hold' em:
{A♣, A♥},
{A♣, A♠},
{A♣, A♦},
{A♥, A♠},
{A♥, A♦} and
{A♠, A♦}.
There are 52 ways to pick the first card and 51 ways to pick the second card and two ways to order the two cards yielding
possible outcomes when being dealt two cards (also ignoring order).
This gives a probability of being dealt two aces of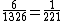
.
The second approach is to use conditional probabilities
, or in more complex situations, a decision tree
. There are 4 ways to be dealt an ace out of 52 choices for the first card resulting in a probability of
There are 3 ways of getting dealt an ace out of 51 choices on the second card after being dealt an ace on the first card for a probability of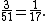 
The conditional probability of being dealt two aces is the product of the two probabilities: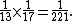 
Often, the key to determining probability is selecting the best approach for a given problem. This article uses both of these approaches.
can be explicitly calculated. In Texas Hold 'em, a player is dealt two down (or hole or pocket) cards. The first card can be any one of 52 playing card
s in the deck and the second card can be any one of the 51 remaining cards. This gives 52 × 51 ÷ 2 = 1,326 possible starting hand combinations. (Since the order in which you receive the first two cards is not significant, the 2,652 permutations are divided by the 2 ways of ordering two cards.) Alternatively, the number of possible starting hands is represented as the binomial coefficient
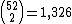
which is the number of possible combination
s of choosing 2 cards from a deck of 52 playing cards.
The 1,326 starting hands can be reduced for purposes of determining the probability of starting hands for Hold 'em—since suits have no relative value in poker, many of these hands are identical in value before the flop. The only factors determining the strength of a starting hand are the ranks of the cards and whether the cards share the same suit. Of the 1,326 combinations, there are 169
distinct starting hands grouped into three shapes: 13 pocket pairs (paired hole cards), 13 × 12 ÷ 2 = 78 suited hands and 78 unsuited hands; 13 + 78 + 78 = 169. The relative probability of being dealt a hand of each given shape is different. The following shows the probabilities and odds of being dealt each type of starting hand.
Here are the probabilities and odds of being dealt various other types of starting hands.
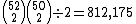
possible head-to-head match ups in Hold 'em. (The total number of match ups is divided by the two ways that two hands can be distributed between two players to give the number of unique match ups.) However, since there are only 169 distinct starting hands, there are 169 × 1,225 = 207,025 distinct head-to-head match ups.
It is useful and interesting to know how two starting hands compete against each other heads up before the flop. In other words, we assume that neither hand will fold, and we will see a showdown. This situation occurs quite often in no limit and tournament play. Also, studying these odds helps to demonstrate the concept of hand domination
, which is important in all community card games.
This problem is considerably more complicated than determining the frequency of dealt hands. To see why, note that given both hands, there are 48 remaining unseen cards. Out of these 48 cards, we can choose any 5 to make a board. Thus, there are
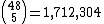
possible boards that may fall. In addition to determining the precise number of boards that give a win to each player, we also must take into account boards which split the pot, and split the number of these boards between the players.
The problem is trivial for computers to solve by brute force search; there are many software programs available that will compute the odds in seconds. A somewhat less trivial exercise is an exhaustive analysis of all of the head-to-head match ups in Texas Hold 'em, which requires evaluating each possible board for each distinct head-to-head match up, or 1,712,304 × 207,025 = 354,489,735,600 (≈354 billion
) results.
in Harrington on Hold'em [p. 125], are summarized in the following table.
These odds are general approximations only derived from averaging all of the hand matchups in each category. The actual head-to-head probabilities for any two starting hands vary depending on a number of factors, including:
For example, A♠ A♣ vs. K♠ Q♣ is 87.65% to win (0.49% to split), but A♠ A♣ vs. 7♦ 6♦ is 76.81% to win (0.32% to split).
The mathematics for computing all of the possible matchups is simple. However, the computation is tedious to carry out by hand. A computer program can perform a brute force evaluation of the 1,712,304 possible boards for any given pair of starting hands in seconds.
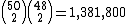
hands. For calculating probabilities we can ignore the distinction between the two opponents holding A♠ J♥ and 8♥ 8♣ and the opponents holding 8♥ 8♣ and A♠ J♥. The number of ways that hands can be distributed between
opponents is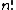 
(the factorial
of n). So the number of unique hand combinations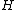
against two opponents is
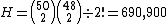
and against three opponents is
and against
opponents is
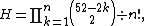or alternatively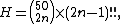 
where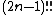
is the number of ways to distribute 
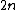cards between 
hands of two cards each. [!! is the double factorial operator: (2n-1)!! is not ((2n-1)!)!.] The following table shows the number of hand combinations for up to nine opponents.
An exhaustive analysis of all of the match ups in Texas Hold 'em of a player against nine opponents requires evaluating each possible board for each distinct starting hand against each possible combination of hands held by nine opponents, which is
(more than 21 octillion).
If you were able to evaluate one trillion (1012) combinations every second, it would take over 670 million years to evaluate all of the hand/board combinations. While it is possible to significantly reduce the total number of combinations by pruning
combinations with identical properties, the total number of situations is still well beyond the number that can be evaluated by brute force. For this reason, most software programs compute probabilities and expected value
s for Hold 'em poker hands against multiple opponents by simulating the play of thousands or even millions of hands to determine statistical probabilities.
. A dominated hand is a hand that is beaten by another hand (the dominant hand) and is extremely unlikely to win against it. Often the dominated hand has only a single card rank that can improve the dominated hand to beat the dominant hand (not counting straights and flushes). For example, KJ is dominated by KQ—both hands share the king, and the queen kicker
is beating the jack kicker. Barring a straight or flush, the KJ will need a jack on the board to improve against the KQ (and would still be losing if a queen appears on the board along with the jack). A pocket pair is dominated by a pocket pair of higher rank.
To calculate the probability that another player has a higher pocket pair, first consider the case against a single opponent. The probability that a single opponent has a higher pair can be stated as the probability that the first card dealt to the opponent is a higher rank than the pocket pair and the second card is the same rank as the first. Where
is the rank of the pocket pair (assigning values from 2–10 and J–A = 11–14), there are (14 − r) × 4 cards of higher rank. Subtracting the two cards for the pocket pair leaves 50 cards in the deck. After the first card is dealt to the player there are 49 cards left, 3 of which are the same rank as the first. So the probability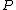 
of a single opponent being dealt a higher pocket pair is
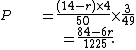
The following approach extends this equation to calculate the probability that one or more other players has a higher pocket pair.
Where
is the number of other players still in the hand and 
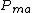is the adjusted probability that multiple opponents have higher pocket pairs, then the probability that at least one of them has a higher pocket pair is
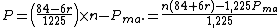
The calculation for
depends on the rank of the player's pocket pair, but can be generalized as
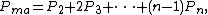
where
is the probability that exactly two players have a higher pair,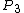 
is the probability that exactly three players have a higher pair, etc. As a practical matter, even with pocket 2s against 9 opponents, 
and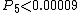 
, so just calculating 
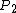and 
gives an adequately precise result.
The following table shows the probability that before the flop another player has a larger pocket pair when there are one to nine other players in the hand.
The following table gives the probability that a hand is facing two or more larger pairs before the flop. From the previous equations, the probability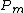
is computed as
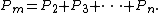
From a practical perspective, however, the odds of out drawing a single pocket pair or multiple pocket pairs are not much different. In both cases the large majority of winning hands require one of the remaining two cards needed to make three of a kind
. The real difference against multiple overpairs becomes the increased probability that one of the overpairs will also make three of a kind.
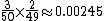. In the case of a table with 
opponents, the probability of one of them holding AA is 
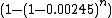. If the player is holding Ax against 9 opponents, there is a probability of approximately 0.0218 that one opponent has AA.
Where
is the rank 2–K of the second card (assigning values from 2–10 and J–K = 11–13) the probability that a single opponent has a better ace is calculated by the formula
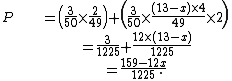
The probability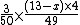
of a player having Ay, where y is a rank such that x < y <= K, is multiplied by the two ways to order the cards A and y in the hand.
The following table shows the probability that before the flop another player has an ace with a larger kicker in the hand.
—for example, if the flop comes with three 2s, any hand holding the fourth 2 has the nuts (though additional cards could still give another player a higher four of a kind or a straight flush). Conversely, the flop can undermine the perceived strength of any hand—a player holding A♣ A♥ would not be happy to see 8♠ 9♠ 10♠ on the flop because of the straight and flush possibilities.
There are
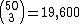
possible flops for any given starting hand. By the turn the total number of combinations has increased to
and on the river there are
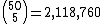
possible boards to go with the hand.
The following are some general probabilities about what can occur on the board. These assume a "random
" starting hand for the player.
An interesting fact to note from the table above is that more than 60% of the flops will have at least two of the same suit—you're likely to either be drawing to a flush or worried about one.
Where
is the rank 3–K of the pocket pair (assigning values from 3–10 and J–K = 11–13), then the number of overcards is 
and the number of cards of rank 
or less is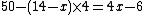 
. The number of outcomes without an overcard is the number of combinations that can be formed with the remaining cards, so the probability 
of an overcard on the flop is
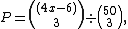
and on the turn and river are
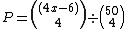and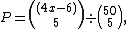 
respectively.
The following table gives the probability that no overcards will come on the flop, turn and river, for each of the pocket pairs from 3 to K.
Notice that there is a better than 35% probability that an ace will come by the river if holding pocket kings, and with pocket queens, the odds are slightly in favor of an ace or a king coming by the turn, and a full 60% in favor of an overcard to the queen by the river. With pocket jacks, there's only a 43% chance that an overcard will not come on the flop and it is better than 3 : 1 that an overcard will come by the river.
Notice, though, that those probabilities would be lower if we consider that at least one opponent happens to hold one of those overcards.
. All situations which have the same number of outs have the same probability of improving to a winning hand over any unimproved hand held by an opponent. For example, an inside straight draw (e.g. 3-4-6-7 missing the 5 for a straight), and a full house draw (e.g. 6-6-K-K drawing for one of the pairs to become three-of-a-kind) are equivalent. Each can be satisfied by four cards—four 5s in the first case, and the other two 6s and other two kings in the second.
The probabilities of drawing these outs are easily calculated. At the flop there remain 47 unseen cards, so the probability is (outs ÷ 47). At the turn there are 46 unseen cards so the probability is (outs ÷ 46). The cumulative probability of making a hand on either the turn or river can be determined as the complement of the odds of not making the hand on the turn and not on the river. The probability of not drawing an out is (47 − outs) ÷ 47 on the turn and (46 − outs) ÷ 46 on the river; taking the complement of these conditional probabilities
gives the probability of drawing the out by the river which is calculated by the formula
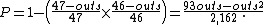
For reference, the probability and odds for some of the more common numbers of outs are given here.
If a player doesn't fold before the river, a hand with at least 14 outs after the flop has a better than 50% chance to catch one of its outs on either the turn or the river. With 20 or more outs, a hand is a better than 2 : 1 favorite to catch at least one out in the two remaining cards.
See the article on pot odds
for examples of how these probabilities might be used in gameplay decisions.
of 3%, a relative average error of 3.5% and a maximum relative error of 6.8%. With one card to come, the percent chance of hitting x is about (x × 2)%. This approximation has a constant relative error of an 8% underestimation, which produces a linearly increasing absolute error of about 1% for each 6 outs.
A slightly more complicated, but significantly more accurate approximation of drawing outs after the flop is to use (x × 4)% for up to 9 outs and (x × 3 + 9)% for 10 or more outs. This approximation has a maximum absolute error of less than 1% for 1 to 19 outs and maximum relative error of less than 5% for 2 to 23 outs. A more accurate approximation for the probability of drawing outs after the turn is (x × 2 + (x × 2) ÷ 10)%. This is easily done by first multiplying x by 2, then rounding the result to the nearest multiple of ten and adding the 10's digit to the first result. For example, 12 outs would be 12 × 2 = 24, 24 rounds to 20, so the approximation is 24 + 2 = 26%. This approximation has a maximum absolute error of less than 0.9% for 1 to 19 outs and a maximum relative error of 3.5% for more than 3 outs. The following shows the approximations and their absolute and relative errors for both methods of approximation.
Either of these approximations is generally accurate enough to aid in most pot odds calculations.
or independent
events.
is the number of common outs, the probability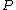 
of drawing runner-runner outs in Texas hold 'em is
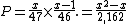
Since a flush would have 10 outs, the probability of a runner-runner flush draw is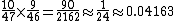
. Other examples of runner-runner draws from a common set of outs are drawing to three or four of a kind. When counting outs, it is convenient to convert runner-runner outs to "normal" outs (see "After the flop"). A runner-runner flush draw is about the equivalent of one "normal" out.
The following table shows the probability and odds of making a runner-runner from a common set of outs and the equivalent normal outs.
After the flop, if
is the number of independent outs for one card and 
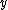is the number of outs for the second card, then the probability 
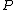of making the runner-runner is
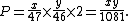
For example, a player holding J♦ Q♦ after the flop 9♥ 5♣ 4♠ needs a 10 and either a K or 8 on the turn and river to make a straight. There are 4 10s and 8 kings and 8s, so the probability is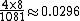
.
The probability of making a conditional runner-runner depends on the condition. For example, a player holding 9♥ 10♥ after the flop 8♦ 2♠ A♣ can make a straight with {J, Q}, {7, J} or {6, 7}. The number of outs for the second card is conditional on the first card—a Q or 6 (8 cards) on the first card leaves only 4 outs (J or 7, respectively) for the second card, while a J or 7 (8 cards) for the first card leaves 8 outs ({Q, 7} or {J, 6}, respectively) for the second card. The probability
of a runner-runner straight for this hand is calculated by the equation
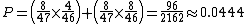
The following table shows the probability and odds of making a runner-runner from a disjoint set of outs for common situations and the equivalent normal outs.
The preceding table assumes the following definitions.
Outside straight and straight flush
Inside+outside straight and straight flush
Inside-only straight and straight flush
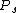is the probability of a runner-runner straight, 
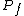is the probability of a runner-runner flush, and 
is the probability of a runner-runner straight flush, then the compound probability 
of getting one of these hands is
The probability of the straight flush is subtracted from the total because it is already included in both the probability of a straight and the probability of a flush, so it has been added twice and must therefore be subtracted from the compound outs of a straight or flush.
The following table gives the compound probability and odds of making a runner-runner for common situations and the equivalent normal outs.
Some hands have even more runner-runner chances to improve. For example, holding the hand J♠ Q♠ after a flop of 10♠ J♥ 7♦ there are several runner-runner hands to make at least a straight. The hand can get two cards from the common outs of {J, Q} (5 cards) to make a full house or four of a kind, can get a J (2 cards) plus either a 7 or 10 (6 cards) to make a full house from these independent disjoint outs, and is drawing to the compound outs of a flush, outside straight or straight flush. The hand can also make {7, 7} or {10, 10} (each drawing from 3 common outs) to make a full house, although this will make four of a kind for anyone holding the remaining 7 or 10 or a bigger full house for anyone holding an overpair. Working from the probabilities from the previous tables and equations, the probability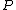
of making one of these runner-runner hands is a compound probability
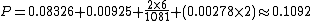
and odds of 8.16 : 1 for the equivalent of 2.59 normal outs. Almost all of these runner-runners give a winning hand against an opponent who had flopped a straight holding 8, 9, but only some give a winning hand against A♠ 2♠ (this hand makes bigger flushes when a flush is hit) or against K♣ Q♦ (this hand makes bigger straights when a straight is hit with 8 9). When counting outs, it is necessary to adjust for which outs are likely to give a winning hand—this is where the skill in poker becomes more important than being able to calculate the probabilities.
Math and probability topics:
Poker
Poker is a family of card games that share betting rules and usually hand rankings. Poker games differ in how the cards are dealt, how hands may be formed, whether the high or low hand wins the pot in a showdown , limits on bet sizes, and how many rounds of betting are allowed.In most modern poker...
, the probability of many events
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
can be determined by direct calculation. This article discusses computing probabilities for many commonly occurring events in the game of Texas hold 'em
Texas hold 'em
Texas Hold 'em is a variation of the standard card game of poker. The game consists of two cards being dealt face down to each player and then five community cards being placed face-up by the dealer—a series of three then two additional single cards , with...
and provides some probabilities
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
for specific situations. In most cases, the probabilities and odds are approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
s due to rounding
Rounding
Rounding a numerical value means replacing it by another value that is approximately equal but has a shorter, simpler, or more explicit representation; for example, replacing $23.4476 with $23.45, or the fraction 312/937 with 1/3, or the expression √2 with 1.414.Rounding is often done on purpose to...
.
When calculating probabilities for a card game such as Texas Hold 'em, there are two basic approaches. The first approach is to determine the number of outcomes that satisfy the condition being evaluated and divide this by the total number of possible outcomes.
For example, there are six outcomes (ignoring order) for being dealt a pair of aces in Hold' em:
{A♣, A♥},
{A♣, A♠},
{A♣, A♦},
{A♥, A♠},
{A♥, A♦} and
{A♠, A♦}.
There are 52 ways to pick the first card and 51 ways to pick the second card and two ways to order the two cards yielding
possible outcomes when being dealt two cards (also ignoring order).This gives a probability of being dealt two aces of
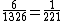.The second approach is to use conditional probabilities
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
, or in more complex situations, a decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
. There are 4 ways to be dealt an ace out of 52 choices for the first card resulting in a probability of
There are 3 ways of getting dealt an ace out of 51 choices on the second card after being dealt an ace on the first card for a probability of 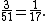The conditional probability of being dealt two aces is the product of the two probabilities: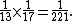 Often, the key to determining probability is selecting the best approach for a given problem. This article uses both of these approaches.
Starting hands
The probability of being dealt various starting handsTexas hold 'em hands
Texas hold 'em starting hands consists of two hole cards in the poker game of Texas hold 'em, which belong solely to the player and remain hidden from the other players. Five community cards are also dealt into play. Betting begins before any of the community cards are exposed, and continues...
can be explicitly calculated. In Texas Hold 'em, a player is dealt two down (or hole or pocket) cards. The first card can be any one of 52 playing card
Playing card
A playing card is a piece of specially prepared heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic, marked with distinguishing motifs and used as one of a set for playing card games...
s in the deck and the second card can be any one of the 51 remaining cards. This gives 52 × 51 ÷ 2 = 1,326 possible starting hand combinations. (Since the order in which you receive the first two cards is not significant, the 2,652 permutations are divided by the 2 ways of ordering two cards.) Alternatively, the number of possible starting hands is represented as the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
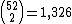
which is the number of possible combination
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s of choosing 2 cards from a deck of 52 playing cards.
The 1,326 starting hands can be reduced for purposes of determining the probability of starting hands for Hold 'em—since suits have no relative value in poker, many of these hands are identical in value before the flop. The only factors determining the strength of a starting hand are the ranks of the cards and whether the cards share the same suit. Of the 1,326 combinations, there are 169
169 (number)
169 is the natural number following 168 and preceding 170.-In mathematics:* 169 is an odd number* 169 is a square number. 13 x 13 = 169, and the reverse 31 x 31 = 961...
distinct starting hands grouped into three shapes: 13 pocket pairs (paired hole cards), 13 × 12 ÷ 2 = 78 suited hands and 78 unsuited hands; 13 + 78 + 78 = 169. The relative probability of being dealt a hand of each given shape is different. The following shows the probabilities and odds of being dealt each type of starting hand.
| Hand shape | Number of hands |
Suit combinations for each hand |
Combinations | Dealt specific hand | Dealt any hand | ||
|---|---|---|---|---|---|---|---|
| Probability | Odds | Probability | Odds | ||||
| Pocket pair | 13 |  |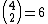
13 × 6 = 78 |  |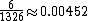
220 : 1 |  |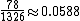
16 : 1 |
| Suited cards | 78 |  |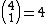
78 × 4 = 312 |  |
331 : 1 |  |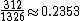
3.25 : 1 |
| Unsuited cards non paired | 78 |  |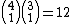
78 × 12 = 936 |  |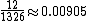
110 : 1 |  |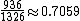
0.417 : 1 |
Here are the probabilities and odds of being dealt various other types of starting hands.
| Hand | Probability | Odds |
|---|---|---|
| AKs (or any specific suited cards) | 0.00302 | 331 : 1 |
| AA (or any specific pair) | 0.00452 | 220 : 1 |
| AKs, KQs, QJs, or JTs (suited cards) | 0.0121 | 81.9 : 1 |
| AK (or any specific non-pair incl. suited) | 0.0121 | 81.9 : 1 |
| AA, KK, or QQ | 0.0136 | 72.7 : 1 |
| AA, KK, QQ or JJ | 0.0181 | 54.3 : 1 |
| Suited cards, jack or better | 0.0181 | 54.3 : 1 |
| AA, KK, QQ, JJ, or TT | 0.0226 | 43.2 : 1 |
| Suited cards, 10 or better | 0.0302 | 32.2 : 1 |
| Suited connectors | 0.0392 | 24.5 : 1 |
| Connected cards, 10 or better | 0.0483 | 19.7 : 1 |
| Any 2 cards with rank at least queen | 0.0498 | 19.1 : 1 |
| Any 2 cards with rank at least jack | 0.0905 | 10.1 : 1 |
| Any 2 cards with rank at least 10 | 0.143 | 5.98 : 1 |
| Connected cards (cards of consecutive rank) | 0.157 | 5.38 : 1 |
| Any 2 cards with rank at least 9 | 0.208 | 3.81 : 1 |
| Not connected nor suited, at least one 2-9 | 0.534 | 0.873 : 1 |
Starting hands heads up
For any given starting hand, there are 50 × 49 ÷ 2 = 1,225 hands that an opponent can have before the flop. (After the flop, the number of possible hands an opponent can have is reduced by the three community cards revealed on the flop to 47 × 46 ÷ 2 = 1,081 hands.) Therefore, there are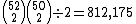possible head-to-head match ups in Hold 'em. (The total number of match ups is divided by the two ways that two hands can be distributed between two players to give the number of unique match ups.) However, since there are only 169 distinct starting hands, there are 169 × 1,225 = 207,025 distinct head-to-head match ups.
It is useful and interesting to know how two starting hands compete against each other heads up before the flop. In other words, we assume that neither hand will fold, and we will see a showdown. This situation occurs quite often in no limit and tournament play. Also, studying these odds helps to demonstrate the concept of hand domination
Domination (poker)
Poker hand A is said to dominate poker hand B if poker hand B has three or fewer outs that would improve it enough to win. Informally, domination is sometimes used to refer to any situation where one hand is highly likely to beat another...
, which is important in all community card games.
This problem is considerably more complicated than determining the frequency of dealt hands. To see why, note that given both hands, there are 48 remaining unseen cards. Out of these 48 cards, we can choose any 5 to make a board. Thus, there are
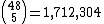
possible boards that may fall. In addition to determining the precise number of boards that give a win to each player, we also must take into account boards which split the pot, and split the number of these boards between the players.
The problem is trivial for computers to solve by brute force search; there are many software programs available that will compute the odds in seconds. A somewhat less trivial exercise is an exhaustive analysis of all of the head-to-head match ups in Texas Hold 'em, which requires evaluating each possible board for each distinct head-to-head match up, or 1,712,304 × 207,025 = 354,489,735,600 (≈354 billion
1000000000 (number)
1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001.In scientific notation, it is written as 109....
) results.
Head-to-head starting hand matchups
When comparing two starting hands, the head-to-head probability describes the likelihood of one hand beating the other after all of the cards have come out. Head-to-head probabilities vary slightly for each particular distinct starting hand matchup, but the approximate average probabilities, as given by Dan HarringtonDan Harrington
Dan Harrington is a professional poker player, best known for winning the main event world championship at the 1995 World Series of Poker. He has earned one World Poker Tour title, two WSOP bracelets, and over six million dollars in tournament cashes in his poker career...
in Harrington on Hold'em [p. 125], are summarized in the following table.
| Favorite-to-underdog matchup | Probability | Odds for |
|---|---|---|
| Pair vs. 2 undercards | 0.83 | 4.9 : 1 |
| Pair vs. lower pair | 0.82 | 4.5 : 1 |
| Pair vs. 1 overcard, 1 undercard | 0.71 | 2.5 : 1 |
| 2 overcards vs. 2 undercards | 0.63 | 1.7 : 1 |
| Pair vs. 2 overcards | 0.55 | 1.2 : 1 |
These odds are general approximations only derived from averaging all of the hand matchups in each category. The actual head-to-head probabilities for any two starting hands vary depending on a number of factors, including:
- Suited or unsuited starting hands;
- Shared suits between starting hands;
- Connectedness of non-pair starting hands;
- Proximity of card ranks between the starting hands (lowering straight potential);
- Proximity of card ranks toward A or 2 (lowering straight potential);
- Possibility of split pot.
For example, A♠ A♣ vs. K♠ Q♣ is 87.65% to win (0.49% to split), but A♠ A♣ vs. 7♦ 6♦ is 76.81% to win (0.32% to split).
The mathematics for computing all of the possible matchups is simple. However, the computation is tedious to carry out by hand. A computer program can perform a brute force evaluation of the 1,712,304 possible boards for any given pair of starting hands in seconds.
Starting hands against multiple opponents
When facing two opponents, for any given starting hand the number of possible combinations of hands the opponents can have is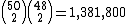hands. For calculating probabilities we can ignore the distinction between the two opponents holding A♠ J♥ and 8♥ 8♣ and the opponents holding 8♥ 8♣ and A♠ J♥. The number of ways that hands can be distributed between
opponents is 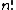(the factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of n). So the number of unique hand combinations
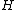against two opponents is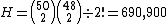and against three opponents is
and against
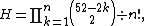opponents is or alternatively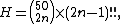 where
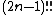is the number of ways to distribute 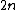cards between hands of two cards each. [!! is the double factorial operator: (2n-1)!! is not ((2n-1)!)!.] The following table shows the number of hand combinations for up to nine opponents.| Opponents | Number of possible hand combinations |
|---|---|
| 1 | 1,225 |
| 2 | 690,900 |
| 3 | 238,360,500 |
| 4 | 56,372,258,250 |
| 5 | ≈9.7073 × 1012 (more than 9 trillion) |
| 6 | ≈1.2620 × 1015 (more than 1 quadrillion) |
| 7 | ≈1.2674 × 1017 (more than 126 quadrillion) |
| 8 | ≈9.9804 × 1018 (almost 10 quintillion) |
| 9 | ≈6.2211 × 1020 (more than 622 quintillion) |
An exhaustive analysis of all of the match ups in Texas Hold 'em of a player against nine opponents requires evaluating each possible board for each distinct starting hand against each possible combination of hands held by nine opponents, which is
(more than 21 octillion).If you were able to evaluate one trillion (1012) combinations every second, it would take over 670 million years to evaluate all of the hand/board combinations. While it is possible to significantly reduce the total number of combinations by pruning
Pruning (algorithm)
Pruning is a technique in machine learning that reduces the size of decision trees by removing sections of the tree that provide little power to classify instances...
combinations with identical properties, the total number of situations is still well beyond the number that can be evaluated by brute force. For this reason, most software programs compute probabilities and expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s for Hold 'em poker hands against multiple opponents by simulating the play of thousands or even millions of hands to determine statistical probabilities.
Dominated hands
When evaluating a hand before the flop, it is useful to have some idea of how likely the hand is dominatedDomination (poker)
Poker hand A is said to dominate poker hand B if poker hand B has three or fewer outs that would improve it enough to win. Informally, domination is sometimes used to refer to any situation where one hand is highly likely to beat another...
. A dominated hand is a hand that is beaten by another hand (the dominant hand) and is extremely unlikely to win against it. Often the dominated hand has only a single card rank that can improve the dominated hand to beat the dominant hand (not counting straights and flushes). For example, KJ is dominated by KQ—both hands share the king, and the queen kicker
Kicker (poker)
A kicker, also called a side card, is a card in a poker hand that does not itself take part in determining the rank of the hand, but that may be used to break ties between hands of the same rank. For example, the hand Q-Q-10-5-2 is ranked as a pair of queens. The 10, 5, and 2 are kickers...
is beating the jack kicker. Barring a straight or flush, the KJ will need a jack on the board to improve against the KQ (and would still be losing if a queen appears on the board along with the jack). A pocket pair is dominated by a pocket pair of higher rank.
Pocket pairs
Barring a straight or flush, a pocket pair needs to make three of a kind to beat a higher pocket pair. See the section "After the flop" for the odds of a pocket pair improving to three of a kind.To calculate the probability that another player has a higher pocket pair, first consider the case against a single opponent. The probability that a single opponent has a higher pair can be stated as the probability that the first card dealt to the opponent is a higher rank than the pocket pair and the second card is the same rank as the first. Where
is the rank of the pocket pair (assigning values from 2–10 and J–A = 11–14), there are (14 − r) × 4 cards of higher rank. Subtracting the two cards for the pocket pair leaves 50 cards in the deck. After the first card is dealt to the player there are 49 cards left, 3 of which are the same rank as the first. So the probability 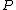of a single opponent being dealt a higher pocket pair is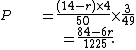The following approach extends this equation to calculate the probability that one or more other players has a higher pocket pair.
- Multiply the base probability for a single player for a given rank of pocket pairs by the number of opponents in the hand;
- Subtract the adjusted probability that more than one opponent has a higher pocket pair. (This is necessary because this probability effectively gets added to the calculation multiple times when multiplying the single player result.
Where
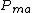is the number of other players still in the hand and is the adjusted probability that multiple opponents have higher pocket pairs, then the probability that at least one of them has a higher pocket pair is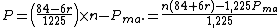The calculation for
depends on the rank of the player's pocket pair, but can be generalized as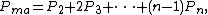where
is the probability that exactly two players have a higher pair, 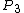is the probability that exactly three players have a higher pair, etc. As a practical matter, even with pocket 2s against 9 opponents, and 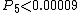, so just calculating 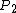and gives an adequately precise result.The following table shows the probability that before the flop another player has a larger pocket pair when there are one to nine other players in the hand.
| Probability of facing a larger pair when holding |
Against 1 | Against 2 | Against 3 | Against 4 | Against 5 | Against 6 | Against 7 | Against 8 | Against 9 |
|---|---|---|---|---|---|---|---|---|---|
| KK | 0.0049 | 0.0098 | 0.0147 | 0.0196 | 0.0244 | 0.0293 | 0.0342 | 0.0391 | 0.0439 |
| 0.0098 | 0.0195 | 0.0292 | 0.0388 | 0.0484 | 0.0579 | 0.0673 | 0.0766 | 0.0859 | |
| JJ | 0.0147 | 0.0292 | 0.0436 | 0.0577 | 0.0717 | 0.0856 | 0.0992 | 0.1127 | 0.1259 |
| TT | 0.0196 | 0.0389 | 0.0578 | 0.0764 | 0.0946 | 0.1124 | 0.1299 | 0.1470 | 0.1637 |
| 99 | 0.0245 | 0.0484 | 0.0718 | 0.0946 | 0.1168 | 0.1384 | 0.1593 | 0.1795 | 0.1990 |
| 88 | 0.0294 | 0.0580 | 0.0857 | 0.1125 | 0.1384 | 0.1634 | 0.1873 | 0.2101 | 0.2318 |
| 77 | 0.0343 | 0.0674 | 0.0994 | 0.1301 | 0.1595 | 0.1874 | 0.2138 | 0.2387 | 0.2619 |
| 66 | 0.0392 | 0.0769 | 0.1130 | 0.1473 | 0.1799 | 0.2104 | 0.2389 | 0.2651 | 0.2890 |
| 55 | 0.0441 | 0.0862 | 0.1263 | 0.1642 | 0.1996 | 0.2324 | 0.2623 | 0.2892 | 0.3129 |
| 44 | 0.0490 | 0.0956 | 0.1395 | 0.1806 | 0.2186 | 0.2532 | 0.2841 | 0.3109 | 0.3334 |
| 33 | 0.0539 | 0.1048 | 0.1526 | 0.1967 | 0.2370 | 0.2729 | 0.3040 | 0.3300 | 0.3503 |
| 22 | 0.0588 | 0.1141 | 0.1654 | 0.2124 | 0.2546 | 0.2914 | 0.3222 | 0.3464 | 0.3633 |
The following table gives the probability that a hand is facing two or more larger pairs before the flop. From the previous equations, the probability
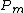is computed as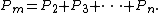| Probability of facing multiple larger pairs when holding |
Against 2 | Against 3 | Against 4 | Against 5 | Against 6 | Against 7 | Against 8 | Against 9 |
|---|---|---|---|---|---|---|---|---|
| KK | < 0.00001 | 0.00001 | 0.00003 | 0.00004 | 0.00007 | 0.00009 | 0.00012 | 0.00016 |
| 0.00006 | 0.00018 | 0.00037 | 0.00061 | 0.00091 | 0.00128 | 0.00171 | 0.00220 | |
| JJ | 0.00017 | 0.00051 | 0.00102 | 0.00171 | 0.00257 | 0.00360 | 0.00482 | 0.00621 |
| TT | 0.00033 | 0.00099 | 0.00200 | 0.00335 | 0.00504 | 0.00709 | 0.00950 | 0.01226 |
| 99 | 0.00054 | 0.00164 | 0.00330 | 0.00553 | 0.00836 | 0.01177 | 0.01580 | 0.02045 |
| 88 | 0.00081 | 0.00244 | 0.00493 | 0.00828 | 0.01253 | 0.01769 | 0.02378 | 0.03084 |
| 77 | 0.00112 | 0.00341 | 0.00689 | 0.01160 | 0.01758 | 0.02487 | 0.03351 | 0.04353 |
| 66 | 0.00149 | 0.00454 | 0.00918 | 0.01550 | 0.02353 | 0.03335 | 0.04503 | 0.05861 |
| 55 | 0.00191 | 0.00583 | 0.01182 | 0.01998 | 0.03040 | 0.04318 | 0.05840 | 0.07619 |
| 44 | 0.00239 | 0.00728 | 0.01480 | 0.02506 | 0.03821 | 0.05438 | 0.07371 | 0.09635 |
| 33 | 0.00291 | 0.00890 | 0.01812 | 0.03075 | 0.04698 | 0.06699 | 0.09099 | 0.11919 |
| 22 | 0.00349 | 0.01068 | 0.02180 | 0.03706 | 0.05673 | 0.08107 | 0.11034 | 0.14484 |
From a practical perspective, however, the odds of out drawing a single pocket pair or multiple pocket pairs are not much different. In both cases the large majority of winning hands require one of the remaining two cards needed to make three of a kind
Three of a Kind
Three of a Kind was a British comedy sketch show starring comedians Tracey Ullman, Lenny Henry and David Copperfield. Three series were made by the BBC between 1981 and 1983....
. The real difference against multiple overpairs becomes the increased probability that one of the overpairs will also make three of a kind.
Hands with one ace
When holding a single ace (referred to as Ax), it is useful to know how likely it is that another player has a better ace—an ace with a higher second card, since a weaker ace is dominated by a better ace. The probability that a single opponent has a better ace is the probability that he has either AA or Ax where x is a rank other than ace that is higher than the player's second card. When holding Ax, the probability that a chosen single player has AA is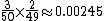. In the case of a table with opponents, the probability of one of them holding AA is . 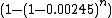If the player is holding Ax against 9 opponents, there is a probability of approximately 0.0218 that one opponent has AA.Where
is the rank 2–K of the second card (assigning values from 2–10 and J–K = 11–13) the probability that a single opponent has a better ace is calculated by the formula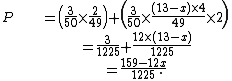The probability
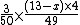of a player having Ay, where y is a rank such that x < y <= K, is multiplied by the two ways to order the cards A and y in the hand.The following table shows the probability that before the flop another player has an ace with a larger kicker in the hand.
| Probability of facing an ace with larger kicker when holding |
Against 1 | Against 2 | Against 3 | Against 4 | Against 5 | Against 6 | Against 7 | Against 8 | Against 9 |
|---|---|---|---|---|---|---|---|---|---|
| AK | 0.00245 | 0.00489 | 0.00733 | 0.00976 | 0.01219 | 0.01460 | 0.01702 | 0.01942 | 0.02183 |
| AQ | 0.01224 | 0.02434 | 0.03629 | 0.04809 | 0.05974 | 0.07126 | 0.08263 | 0.09386 | 0.10496 |
| AJ | 0.02204 | 0.04360 | 0.06468 | 0.08529 | 0.10545 | 0.12517 | 0.14445 | 0.16331 | 0.18175 |
| AT | 0.03184 | 0.06266 | 0.09250 | 0.12139 | 0.14937 | 0.17645 | 0.20267 | 0.22805 | 0.25263 |
| A9 | 0.04163 | 0.08153 | 0.11977 | 0.15642 | 0.19154 | 0.22520 | 0.25745 | 0.28837 | 0.31799 |
| A8 | 0.05143 | 0.10021 | 0.14649 | 0.19038 | 0.23202 | 0.27152 | 0.30898 | 0.34452 | 0.37823 |
| A7 | 0.06122 | 0.11870 | 0.17266 | 0.22331 | 0.27086 | 0.31550 | 0.35741 | 0.39675 | 0.43369 |
| A6 | 0.07102 | 0.13700 | 0.19829 | 0.25523 | 0.30812 | 0.35726 | 0.40291 | 0.44531 | 0.48471 |
| A5 | 0.08082 | 0.15510 | 0.22338 | 0.28615 | 0.34384 | 0.39687 | 0.44561 | 0.49041 | 0.53160 |
| A4 | 0.09061 | 0.17301 | 0.24795 | 0.31609 | 0.37806 | 0.43442 | 0.48567 | 0.53227 | 0.57465 |
| A3 | 0.10041 | 0.19073 | 0.27199 | 0.34509 | 0.41085 | 0.47000 | 0.52322 | 0.57109 | 0.61416 |
| A2 | 0.11020 | 0.20826 | 0.29552 | 0.37315 | 0.44223 | 0.50370 | 0.55840 | 0.60706 | 0.65037 |
The flop
The value of a starting hand can change dramatically after the flop. Regardless of initial strength, any hand can flop the nutsNut hand
In poker, the nut hand, is the strongest possible hand in a given situation. The second-nut hand or third-nut hand may refer to the second and third best possible hands...
—for example, if the flop comes with three 2s, any hand holding the fourth 2 has the nuts (though additional cards could still give another player a higher four of a kind or a straight flush). Conversely, the flop can undermine the perceived strength of any hand—a player holding A♣ A♥ would not be happy to see 8♠ 9♠ 10♠ on the flop because of the straight and flush possibilities.
There are
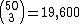
possible flops for any given starting hand. By the turn the total number of combinations has increased to
and on the river there are
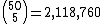
possible boards to go with the hand.
The following are some general probabilities about what can occur on the board. These assume a "random
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
" starting hand for the player.
| Board consisting of | Making on flop | Making by turn | Making by river | |||
|---|---|---|---|---|---|---|
| Prob. | Odds | Prob. | Odds | Prob. | Odds | |
| Three or more of same suit | 0.05177 | 18.3 : 1 | 0.13522 | 6.40 : 1 | 0.23589 | 3.24 : 1 |
| Four or more of same suit | 0.01056 | 93.7 : 1 | 0.03394 | 28.5 : 1 | ||
| Rainbow flop (all different suits) | 0.39765 | 1.51 : 1 | 0.10550 | 8.48 : 1 | ||
| Three cards of consecutive rank (but not four consecutive) | 0.03475 | 27.8 : 1 | 0.11820 | 7.46 : 1 | 0.25068 | 2.99 : 1 |
| Four cards to a straight (but not five) | 0.03877 | 24.8 : 1 | 0.18991 | 4.27 : 1 | ||
| Three or more cards of consecutive rank and same suit | 0.00217 | 459 : 1 | 0.00869 | 114 : 1 | 0.02172 | 45.0 : 1 |
| Three of a kind (but not a full house or four of a kind) | 0.00235 | 424 : 1 | 0.00935 | 106 : 1 | 0.02128 | 46 : 1 |
| A pair (but not two pair or three or four of a kind) | 0.16941 | 4.90 : 1 | 0.30417 | 2.29 : 1 | 0.42450 | 1.36 : 1 |
| Two pair (but not a full house) | 0.01037 | 95.4 : 1 | 0.04716 | 20.2 : 1 |
An interesting fact to note from the table above is that more than 60% of the flops will have at least two of the same suit—you're likely to either be drawing to a flush or worried about one.
Flopping overcards when holding a pocket pair
It is also useful to look at the chances different starting hands have of either improving on the flop, or of weakening on the flop. One interesting circumstance concerns pocket pairs. When holding a pocket pair, overcards (cards of higher rank than the pair) weaken the hand because of the potential that an overcard has paired a card in an opponent's hand. The hand gets worse the more overcards there are on the board and the more opponents that are in the hand because the probability that one of the overcards has paired a hole card increases. To calculate the probability of no overcard, take the total number of outcomes without an overcard divided by the total number of outcomes.Where
is the rank 3–K of the pocket pair (assigning values from 3–10 and J–K = 11–13), then the number of overcards is and the number of cards of rank or less is 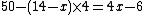. The number of outcomes without an overcard is the number of combinations that can be formed with the remaining cards, so the probability of an overcard on the flop is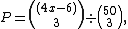and on the turn and river are
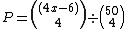and 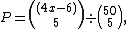respectively.The following table gives the probability that no overcards will come on the flop, turn and river, for each of the pocket pairs from 3 to K.
| Holding pocket pair | No overcard on flop | No overcard by turn | No overcard by river | |||
|---|---|---|---|---|---|---|
| Prob. | Odds | Prob. | Odds | Prob. | Odds | |
| KK | 0.7745 | 0.29 : 1 | 0.7086 | 0.41 : 1 | 0.6470 | 0.55 : 1 |
| 0.5857 | 0.71 : 1 | 0.4860 | 1.06 : 1 | 0.4015 | 1.49 : 1 | |
| JJ | 0.4304 | 1.32 : 1 | 0.3205 | 2.12 : 1 | 0.2369 | 3.22 : 1 |
| TT | 0.3053 | 2.28 : 1 | 0.2014 | 3.97 : 1 | 0.1313 | 6.61 : 1 |
| 99 | 0.2071 | 3.83 : 1 | 0.1190 | 7.40 : 1 | 0.0673 | 13.87 : 1 |
| 88 | 0.1327 | 6.54 : 1 | 0.0649 | 14.40 : 1 | 0.0310 | 31.21 : 1 |
| 77 | 0.0786 | 11.73 : 1 | 0.0318 | 30.48 : 1 | 0.0124 | 79.46 : 1 |
| 66 | 0.0416 | 23.02 : 1 | 0.0133 | 74.26 : 1 | 0.0040 | 246.29 : 1 |
| 55 | 0.0186 | 52.85 : 1 | 0.0043 | 229.07 : 1 | 0.0009 | 1,057.32 : 1 |
| 44 | 0.0061 | 162.33 : 1 | 0.0009 | 1,095.67 : 1 | 0.0001 | 8,406.78 : 1 |
| 33 | 0.0010 | 979.00 : 1 | 0.0001 | 15,352.33 : 1 | 0.0000 | 353,125.67 : 1 |
Notice that there is a better than 35% probability that an ace will come by the river if holding pocket kings, and with pocket queens, the odds are slightly in favor of an ace or a king coming by the turn, and a full 60% in favor of an overcard to the queen by the river. With pocket jacks, there's only a 43% chance that an overcard will not come on the flop and it is better than 3 : 1 that an overcard will come by the river.
Notice, though, that those probabilities would be lower if we consider that at least one opponent happens to hold one of those overcards.
After the flop – outs
During play—that is, from the flop and onwards—drawing probabilities come down to a question of outsOut (poker)
In a poker game with more than one betting round, an out is any unseen card that, if drawn, will improve a player's hand to one that is likely to win. Knowing the number of outs a player has is an important part of poker strategy. For example in draw poker, a hand with four diamonds has nine outs...
. All situations which have the same number of outs have the same probability of improving to a winning hand over any unimproved hand held by an opponent. For example, an inside straight draw (e.g. 3-4-6-7 missing the 5 for a straight), and a full house draw (e.g. 6-6-K-K drawing for one of the pairs to become three-of-a-kind) are equivalent. Each can be satisfied by four cards—four 5s in the first case, and the other two 6s and other two kings in the second.
The probabilities of drawing these outs are easily calculated. At the flop there remain 47 unseen cards, so the probability is (outs ÷ 47). At the turn there are 46 unseen cards so the probability is (outs ÷ 46). The cumulative probability of making a hand on either the turn or river can be determined as the complement of the odds of not making the hand on the turn and not on the river. The probability of not drawing an out is (47 − outs) ÷ 47 on the turn and (46 − outs) ÷ 46 on the river; taking the complement of these conditional probabilities
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
gives the probability of drawing the out by the river which is calculated by the formula
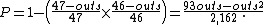
For reference, the probability and odds for some of the more common numbers of outs are given here.
| Example drawing to | Outs | Make on turn | Make on river | Make on turn or river | |||
|---|---|---|---|---|---|---|---|
| Prob. | Odds | Prob. | Odds | Prob. | Odds | ||
| Inside straight flush Straight Flush Straight Flush was the name of a B-29 Superfortress participating in the atomic bomb attack on Hiroshima on August 6, 1945.... ; Four of a kind Four of a Kind Four of a Kind is the debut feature film for director Fiona Cochrane. It was completed in 2008 and released in 2009.It is based on the stage play Disclosure by Helen Collins as presented at La Mama Theatre during the 2006 Melbourne Fringe Festival. It was shot on location in Melbourne,... |
1 | 0.0213 | 46.0 : 1 | 0.0217 | 45.0 : 1 | 0.0426 | 22.5 : 1 |
| Open-ended Open-ended (poker) Open-ended refers to a situation in poker where the player has four of five cards needed for a straight that can be completed at either end. For example, a player with 3♥ 4♥ 5♣ 6♠ is open-ended, because a deuce or a seven would give the player a straight... straight flush; Three of a kind Three of a Kind Three of a Kind was a British comedy sketch show starring comedians Tracey Ullman, Lenny Henry and David Copperfield. Three series were made by the BBC between 1981 and 1983.... |
2 | 0.0426 | 22.5 : 1 | 0.0435 | 22.0 : 1 | 0.0842 | 10.9 : 1 |
| High pair | 3 | 0.0638 | 14.7 : 1 | 0.0652 | 14.3 : 1 | 0.1249 | 7.01 : 1 |
| Inside straight; Full house | 4 | 0.0851 | 10.7 : 1 | 0.0870 | 10.5 : 1 | 0.1647 | 5.07 : 1 |
| Three of a kind or two pair | 5 | 0.1064 | 8.40 : 1 | 0.1087 | 8.20 : 1 | 0.2035 | 3.91 : 1 |
| Either pair | 6 | 0.1277 | 6.83 : 1 | 0.1304 | 6.67 : 1 | 0.2414 | 3.14 : 1 |
| Full house or four of a kind; Inside straight or high pair |
7 | 0.1489 | 5.71 : 1 | 0.1522 | 5.57 : 1 | 0.2784 | 2.59 : 1 |
| Open-ended straight | 8 | 0.1702 | 4.88 : 1 | 0.1739 | 4.75 : 1 | 0.3145 | 2.18 : 1 |
| Flush | 9 | 0.1915 | 4.22 : 1 | 0.1957 | 4.11 : 1 | 0.3497 | 1.86 : 1 |
| Inside straight or pair | 10 | 0.2128 | 3.70 : 1 | 0.2174 | 3.60 : 1 | 0.3839 | 1.60 : 1 |
| Open-ended straight or high pair | 11 | 0.2340 | 3.27 : 1 | 0.2391 | 3.18 : 1 | 0.4172 | 1.40 : 1 |
| Inside straight or flush; Flush or high pair | 12 | 0.2553 | 2.92 : 1 | 0.2609 | 2.83 : 1 | 0.4496 | 1.22 : 1 |
| 13 | 0.2766 | 2.62 : 1 | 0.2826 | 2.54 : 1 | 0.4810 | 1.08 : 1 | |
| Open-ended straight or pair | 14 | 0.2979 | 2.36 : 1 | 0.3043 | 2.29 : 1 | 0.5116 | 0.955 : 1 |
| Open-ended straight or flush; Flush or pair; Inside straight, flush or high pair |
15 | 0.3191 | 2.13 : 1 | 0.3261 | 2.07 : 1 | 0.5412 | 0.848 : 1 |
| 16 | 0.3404 | 1.94 : 1 | 0.3478 | 1.88 : 1 | 0.5698 | 0.755 : 1 | |
| 17 | 0.3617 | 1.76 : 1 | 0.3696 | 1.71 : 1 | 0.5976 | 0.673 : 1 | |
| Inside straight or flush or pair; Open-ended straight, flush or high pair |
18 | 0.3830 | 1.61 : 1 | 0.3913 | 1.56 : 1 | 0.6244 | 0.601 : 1 |
| 19 | 0.4043 | 1.47 : 1 | 0.4130 | 1.42 : 1 | 0.6503 | 0.538 : 1 | |
| 20 | 0.4255 | 1.35 : 1 | 0.4348 | 1.30 : 1 | 0.6753 | 0.481 : 1 | |
| Open-ended straight, flush or pair | 21 | 0.4468 | 1.24 : 1 | 0.4565 | 1.19 : 1 | 0.6994 | 0.430 : 1 |
- When drawing to a full house or four of a kind with a pocket pair that has hit trips (three of a kind) on the flop, there are 6 outs to get a full house by pairing the board and one out to make four of a kind. This means that if the turn does not pair the board or make four of a kind, there will be 3 additional outs on the river, for a total of 10, to pair the turn card and make a full house. This makes the probability of drawing to a full house or four of a kind on the turn or river 0.334 and the odds are 1.99 : 1. This makes drawing to a full house or four of a kind by the river about 8½ outs.
If a player doesn't fold before the river, a hand with at least 14 outs after the flop has a better than 50% chance to catch one of its outs on either the turn or the river. With 20 or more outs, a hand is a better than 2 : 1 favorite to catch at least one out in the two remaining cards.
See the article on pot odds
Pot odds
In poker, pot odds are the ratio of the current size of the pot to the cost of a contemplated call. Pot odds are often compared to the probability of winning a hand with a future card in order to estimate the call's expected value....
for examples of how these probabilities might be used in gameplay decisions.
Estimating probability of drawing outs - The rule of four and two
Many poker players do not have the mathematical ability to calculate odds in the middle of a poker hand. One solution is to just memorize the odds of drawing outs at the river and turn since these odds are needed frequently for making decisions. Another solution some players use is an easily calculated approximation of the probability for drawing outs, commonly referred to as the "Rule of Four and Two". With two cards to come, the percent chance of hitting x outs is about (x × 4)%. This approximation gives roughly accurate probabilities up to about 12 outs after the flop, with an absolute average error of 0.9%, a maximum absolute errorApproximation error
The approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because#the measurement of the data is not precise due to the instruments...
of 3%, a relative average error of 3.5% and a maximum relative error of 6.8%. With one card to come, the percent chance of hitting x is about (x × 2)%. This approximation has a constant relative error of an 8% underestimation, which produces a linearly increasing absolute error of about 1% for each 6 outs.
A slightly more complicated, but significantly more accurate approximation of drawing outs after the flop is to use (x × 4)% for up to 9 outs and (x × 3 + 9)% for 10 or more outs. This approximation has a maximum absolute error of less than 1% for 1 to 19 outs and maximum relative error of less than 5% for 2 to 23 outs. A more accurate approximation for the probability of drawing outs after the turn is (x × 2 + (x × 2) ÷ 10)%. This is easily done by first multiplying x by 2, then rounding the result to the nearest multiple of ten and adding the 10's digit to the first result. For example, 12 outs would be 12 × 2 = 24, 24 rounds to 20, so the approximation is 24 + 2 = 26%. This approximation has a maximum absolute error of less than 0.9% for 1 to 19 outs and a maximum relative error of 3.5% for more than 3 outs. The following shows the approximations and their absolute and relative errors for both methods of approximation.
| Outs | Make on turn or river | Make on river | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual | (x × 4)% | (x × 3 + 9)% | Actual | (x × 2)% | (x × 2 + (x × 2) ÷ 10)% | |||||||||
| Est. | Error | % Error | Est. | Error | % Error | Est. | Error | % Error | Est. | Error | % Error | |||
| 1 | 4.2553% | 4% | −0.26% | 6.00% | 4% | −0.26% | 6.00% | 2.1739% | 2% | −0.17% | 8.00% | 2% | −0.17% | 8.00% |
| 2 | 8.4181% | 8% | −0.42% | 4.97% | 8% | −0.42% | 4.97% | 4.3478% | 4% | −0.35% | 8.00% | 4% | −0.35% | 8.00% |
| 3 | 12.4884% | 12% | −0.49% | 3.91% | 12% | −0.49% | 3.91% | 6.5217% | 6% | −0.52% | 8.00% | 7% | 7.33% | |
| 4 | 16.4662% | 16% | −0.47% | 2.83% | 16% | −0.47% | 2.83% | 8.6957% | 8% | −0.70% | 8.00% | 9% | 3.50% | |
| 5 | 20.3515% | 20% | −0.35% | 1.73% | 20% | −0.35% | 1.73% | 10.8696% | 10% | −0.87% | 8.00% | 11% | 1.20% | |
| 6 | 24.1443% | 24% | −0.14% | 0.60% | 24% | −0.14% | 0.60% | 13.0435% | 12% | −1.04% | 8.00% | 13% | −0.04% | 0.33% |
| 7 | 27.8446% | 28% | +0.16% | 0.56% | 28% | 0.56% | 15.2174% | 14% | −1.22% | 8.00% | 15% | −0.22% | 1.43% | |
| 8 | 31.4524% | 32% | +0.55% | 1.74% | 32% | 1.74% | 17.3913% | 16% | −1.39% | 8.00% | 18% | 3.50% | ||
| 9 | 34.9676% | 36% | +1.03% | 2.95% | 36% | 2.95% | 19.5652% | 18% | −1.57% | 8.00% | 20% | 2.22% | ||
| 10 | 38.3904% | 40% | +1.61% | 4.19% | 39% | 1.59% | 21.7391% | 20% | −1.74% | 8.00% | 22% | 1.20% | ||
| 11 | 41.7206% | 44% | +2.28% | 5.46% | 42% | 0.67% | 23.9130% | 22% | −1.91% | 8.00% | 24% | 0.36% | ||
| 12 | 44.9584% | 48% | +3.04% | 6.77% | 45% | 0.09% | 26.0870% | 24% | −2.09% | 8.00% | 26% | −0.09% | 0.33% | |
| 13 | 48.1036% | 52% | +3.90% | 8.10% | 48% | −0.10% | 0.22% | 28.2609% | 26% | −2.26% | 8.00% | 29% | 2.62% | |
| 14 | 51.1563% | 56% | +4.84% | 9.47% | 51% | −0.16% | 0.31% | 30.4348% | 28% | −2.43% | 8.00% | 31% | 1.86% | |
| 15 | 54.1166% | 60% | +5.88% | 10.87% | 54% | −0.12% | 0.22% | 32.6087% | 30% | −2.61% | 8.00% | 33% | 1.20% | |
| 16 | 56.9843% | 64% | +7.02% | 12.31% | 57% | 0.03% | 34.7826% | 32% | −2.78% | 8.00% | 35% | 0.62% | ||
| 17 | 59.7595% | 68% | +8.24% | 13.79% | 60% | 0.40% | 36.9565% | 34% | −2.96% | 8.00% | 37% | 0.12% | ||
| 18 | 62.4422% | 72% | +9.56% | 15.31% | 63% | 0.89% | 39.1304% | 36% | −3.13% | 8.00% | 40% | 2.22% | ||
| 19 | 65.0324% | 76% | 16.86% | 66% | 1.49% | 41.3043% | 38% | −3.30% | 8.00% | 42% | 1.68% | |||
| 20 | 67.5301% | 80% | 18.47% | 69% | 2.18% | 43.4783% | 40% | −3.48% | 8.00% | 44% | 1.20% | |||
| 21 | 69.9352% | 84% | 20.11% | 72% | 2.95% | 45.6522% | 42% | −3.65% | 8.00% | 46% | 0.76% | |||
| 22 | 72.2479% | 88% | 21.80% | 75% | 3.81% | 47.8261% | 44% | −3.83% | 8.00% | 48% | 0.36% | |||
| 23 | 74.4681% | 92% | 23.54% | 78% | 4.74% | 50.0000% | 46% | −4.00% | 8.00% | 51% | 2.00% | |||
Either of these approximations is generally accurate enough to aid in most pot odds calculations.
Runner-runner outs
Some outs for a hand require drawing an out on both the turn and the river—making two consecutive outs is called a runner-runner. Examples would be needing two cards to make a straight, flush, or three or four of a kind. Runner-runner outs can either draw from a common set of outs or from disjoint sets of outs. Two disjoint outs can either be conditionalConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
or independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
events.
Common outs
Drawing to a flush is an example of drawing from a common set of outs. Both the turn and river need to be the same suit, so both outs are coming from a common set of outs—the set of remaining cards of the desired suit. After the flop, if is the number of common outs, the probability 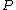of drawing runner-runner outs in Texas hold 'em is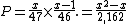Since a flush would have 10 outs, the probability of a runner-runner flush draw is
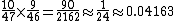. Other examples of runner-runner draws from a common set of outs are drawing to three or four of a kind. When counting outs, it is convenient to convert runner-runner outs to "normal" outs (see "After the flop"). A runner-runner flush draw is about the equivalent of one "normal" out.The following table shows the probability and odds of making a runner-runner from a common set of outs and the equivalent normal outs.
| Likely drawing to | Common outs | Probability | Odds | Equivalent outs |
|---|---|---|---|---|
| Four of a kind (with pair) Inside-only straight flush |
2 | 0.00093 | 1,080 : 1 | 0.02 |
| Three of a kind (with no pair) | 3 | 0.00278 | 359 : 1 | 0.07 |
| 4 | 0.00556 | 179 : 1 | 0.13 | |
| 5 | 0.00925 | 107 : 1 | 0.22 | |
| Two pair or three of a kind (with no pair) | 6 | 0.01388 | 71.1 : 1 | 0.33 |
| 7 | 0.01943 | 50.5 : 1 | 0.46 | |
| 8 | 0.02590 | 37.6 : 1 | 0.61 | |
| 9 | 0.03330 | 29.0 : 1 | 0.78 | |
| Flush | 10 | 0.04163 | 23.0 : 1 | 0.98 |
Disjoint outs
Two outs are disjoint when there are no common cards between the set of cards needed for the first out and the set of cards needed for the second out. The outs are independent of each other if it does not matter which card comes first, and one card appearing does not affect the probability of the other card appearing except by changing the number of remaining cards; an example is drawing two cards to an inside straight. The outs are conditional on each other if the number of outs available for the second card depends on the first card; an example is drawing two cards to an outside straight.After the flop, if
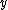is the number of independent outs for one card and is the number of outs for the second card, then the probability 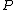of making the runner-runner is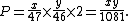For example, a player holding J♦ Q♦ after the flop 9♥ 5♣ 4♠ needs a 10 and either a K or 8 on the turn and river to make a straight. There are 4 10s and 8 kings and 8s, so the probability is
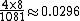.The probability of making a conditional runner-runner depends on the condition. For example, a player holding 9♥ 10♥ after the flop 8♦ 2♠ A♣ can make a straight with {J, Q}, {7, J} or {6, 7}. The number of outs for the second card is conditional on the first card—a Q or 6 (8 cards) on the first card leaves only 4 outs (J or 7, respectively) for the second card, while a J or 7 (8 cards) for the first card leaves 8 outs ({Q, 7} or {J, 6}, respectively) for the second card. The probability
of a runner-runner straight for this hand is calculated by the equation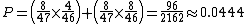The following table shows the probability and odds of making a runner-runner from a disjoint set of outs for common situations and the equivalent normal outs.
| Drawing to | Probability | Odds | Equivalent outs |
|---|---|---|---|
| Outside straight | 0.04440 | 21.5 : 1 | 1.04 |
| Inside+outside straight | 0.02960 | 32.8 : 1 | 0.70 |
| Inside-only straight | 0.01480 | 66.6 : 1 | 0.35 |
| Outside straight flush | 0.00278 | 359 : 1 | 0.07 |
| Inside+outside straight flush | 0.00185 | 540 : 1 | 0.04 |
The preceding table assumes the following definitions.
Outside straight and straight flush
- Drawing to a sequence of three cards of consecutive rank from 3-4-5 to 10-J-Q where two cards can be added to either end of the sequence to make a straight or straight flush.
Inside+outside straight and straight flush
- Drawing to a straight or straight flush where one required rank can be combined with one of two other ranks to make the hand. This includes sequences like 5-7-8 which requires a 6 plus either a 4 or 9 as well as the sequences J-Q-K, which requires a 10 plus either a 9 or A, and 2-3-4 which requires a 5 plus either an A or 6.
Inside-only straight and straight flush
- Drawing to a straight or straight flush where there are only two ranks that make the hand. This includes hands such as 5-7-9 which requires a 6 and an 8 as well as A-2-3 which requires a 4 and a 5.
Compound outs
The strongest runner-runner probabilities lie with hands that are drawing to multiple hands with different runner-runner combinations. These include hands that can make a straight, flush or straight flush, as well as four of a kind or a full house. Calculating these probabilities requires adding the compound probabilities for the various outs, taking care to account for any shared hands. For example, if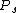 is the probability of a runner-runner straight, 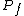is the probability of a runner-runner flush, and is the probability of a runner-runner straight flush, then the compound probability of getting one of these hands isThe probability of the straight flush is subtracted from the total because it is already included in both the probability of a straight and the probability of a flush, so it has been added twice and must therefore be subtracted from the compound outs of a straight or flush.
The following table gives the compound probability and odds of making a runner-runner for common situations and the equivalent normal outs.
| Drawing to | Probability | Odds | Equivalent outs |
|---|---|---|---|
| Flush, outside straight or straight flush | 0.08326 | 11.0 : 1 | 1.98 |
| Flush, inside+outside straight or straight flush | 0.06938 | 13.4 : 1 | 1.65 |
| Flush, inside-only straight or straight flush | 0.05550 | 17.0 : 1 | 1.30 |
Some hands have even more runner-runner chances to improve. For example, holding the hand J♠ Q♠ after a flop of 10♠ J♥ 7♦ there are several runner-runner hands to make at least a straight. The hand can get two cards from the common outs of {J, Q} (5 cards) to make a full house or four of a kind, can get a J (2 cards) plus either a 7 or 10 (6 cards) to make a full house from these independent disjoint outs, and is drawing to the compound outs of a flush, outside straight or straight flush. The hand can also make {7, 7} or {10, 10} (each drawing from 3 common outs) to make a full house, although this will make four of a kind for anyone holding the remaining 7 or 10 or a bigger full house for anyone holding an overpair. Working from the probabilities from the previous tables and equations, the probability
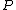of making one of these runner-runner hands is a compound probability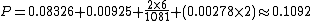and odds of 8.16 : 1 for the equivalent of 2.59 normal outs. Almost all of these runner-runners give a winning hand against an opponent who had flopped a straight holding 8, 9, but only some give a winning hand against A♠ 2♠ (this hand makes bigger flushes when a flush is hit) or against K♣ Q♦ (this hand makes bigger straights when a straight is hit with 8 9). When counting outs, it is necessary to adjust for which outs are likely to give a winning hand—this is where the skill in poker becomes more important than being able to calculate the probabilities.
See also
Poker topics:- Poker probabilityPoker probabilityIn poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands.-Frequency of 5-card poker hands:...
- Poker strategyPoker strategyPoker is a popular card game that combines elements of chance and strategy. There are various styles of poker, all of which share an objective of presenting the least probable or highest-scoring hand. A poker hand is a configuration of five cards, either held entirely by a player or drawn partly...
Math and probability topics:
- Sample space
- PermutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
- Combinatorial game theoryCombinatorial game theoryCombinatorial game theory is a branch of applied mathematics and theoretical computer science that studies sequential games with perfect information, that is, two-player games which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning...
- Game complexityGame complexityCombinatorial game theory has several ways of measuring game complexity. This article describes five of them: state-space complexity, game tree size, decision complexity, game-tree complexity, and computational complexity.-Measures of game complexity:...
- Set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
- Gaming mathematicsGaming mathematicsGaming mathematics, also referred to as the mathematics of gambling, is a collection of probability applications encountered in games of chance and can be included in applied mathematics...
External links
- Poker Computations by Brian Alspach