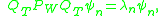Prolate spheroidal wave functions
Encyclopedia
In mathematics, the prolate spheroidal wave functions are a set of functions derived by timelimiting and lowpassing, and a second timelimit operation. Let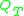 
denote the time truncation operator, such that 
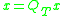iff x is timelimited within 
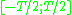. Similarly, let 
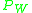denote an ideal low-pass filtering operator, such that 
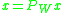iff x is bandlimited within 
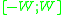. The operator 
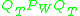turns out to be linear, bounded and self-adjoint
. For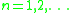
we denote with 
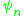the n-th eigenfunction
, defined as
where
are the associated eigenvalues. The timelimited functions 
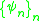are the Prolate Spheroidal Wave Functions (PSWFs).
These functions are also encountered in a different context. When solving the Helmholtz equation
,
, by the method of separation of variables in prolate spheroidal coordinates
,
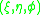, with:
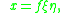
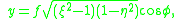
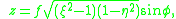
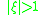and 
.
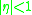the solution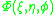
can be written
as the product of a radial spheroidal wavefunction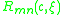
and an angular spheroidal wavefunction 
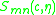by 
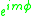with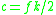 
.
The radial wavefunction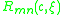
satisfies the linear ordinary differential equation
:
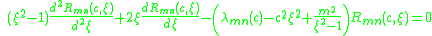
The eigenvalue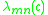
of this Sturm-Liouville differential equation is fixed by the requirement that 
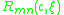must be finite for 
.
The angular wavefunction satisfies the differential equation:
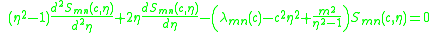
It is the same differential equation as in the case of the radial wavefunction. However, the range of the variable is different (in the radial wavefunction,
) in the angular wavefunction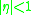 
).
For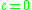
these two differential equations reduce to the equations satisfied by the associated Legendre polynomials
. For
, the angular spheroidal wavefunctions can be expanded as a series of Legendre functions.
Let us note that if one writes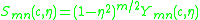
, the function 
satisfies the following linear ordinary differential equation:
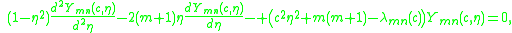
which is known as the spheroidal wave equation. This auxiliary equation is used for instance by Stratton in his 1935 article.
There are different normalization schemes for spheroidal functions. A table of the different schemes can be found in Abramowitz and Stegun p. 758. Abramowitz and Stegun (and the present article) follow the notation of Flammer.
In the case of oblate spheroidal coordinates
the solution of the Helmholtz equation yields oblate spheroidal wavefunctions.
Originally, the spheroidal wave functions were introduced by C. Niven in 1880 when studying the conduction of heat in an ellipsoid of revolution, which lead to a Helmholtz equation in spheroidal coordinates.
Prolate spheroidal wave functions whose domain is a (portion of) the surface of the unit sphere are more generally called "Slepian functions" (see also Spectral concentration problem
). These are of great utility in disciplines such as geodesy or cosmology.
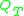denote the time truncation operator, such that 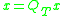iff x is timelimited within 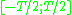. Similarly, let 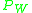denote an ideal low-pass filtering operator, such that 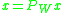iff x is bandlimited within 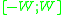. The operator 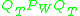turns out to be linear, bounded and self-adjointSelf-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
. For
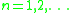we denote with 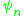the n-th eigenfunctionEigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
, defined as
where
are the associated eigenvalues. The timelimited functions 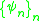are the Prolate Spheroidal Wave Functions (PSWFs).These functions are also encountered in a different context. When solving the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
,
, by the method of separation of variables in prolate spheroidal coordinatesProlate spheroidal coordinates
Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating a spheroid around its major axis, i.e., the axis on which the foci are located...
,
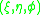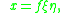
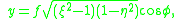
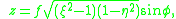
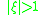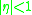, with: and .the solution
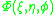can be writtenas the product of a radial spheroidal wavefunction
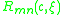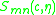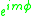and an angular spheroidal wavefunction by with 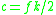.The radial wavefunction
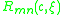satisfies the linear ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
:
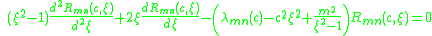
The eigenvalue
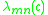of this Sturm-Liouville differential equation is fixed by the requirement that 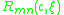must be finite for .The angular wavefunction satisfies the differential equation:
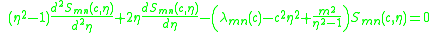
It is the same differential equation as in the case of the radial wavefunction. However, the range of the variable is different (in the radial wavefunction,
) in the angular wavefunction 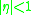).For
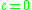these two differential equations reduce to the equations satisfied by the associated Legendre polynomialsAssociated Legendre polynomials
In mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
. For
, the angular spheroidal wavefunctions can be expanded as a series of Legendre functions.Let us note that if one writes
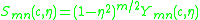, the function satisfies the following linear ordinary differential equation: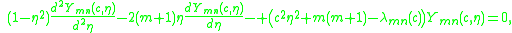which is known as the spheroidal wave equation. This auxiliary equation is used for instance by Stratton in his 1935 article.
There are different normalization schemes for spheroidal functions. A table of the different schemes can be found in Abramowitz and Stegun p. 758. Abramowitz and Stegun (and the present article) follow the notation of Flammer.
In the case of oblate spheroidal coordinates
Oblate spheroidal coordinates
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of...
the solution of the Helmholtz equation yields oblate spheroidal wavefunctions.
Originally, the spheroidal wave functions were introduced by C. Niven in 1880 when studying the conduction of heat in an ellipsoid of revolution, which lead to a Helmholtz equation in spheroidal coordinates.
Prolate spheroidal wave functions whose domain is a (portion of) the surface of the unit sphere are more generally called "Slepian functions" (see also Spectral concentration problem
Spectral concentration problem
The spectral concentration problem in Fourier analysis refers to finding a time sequence whose discrete Fourier transform is maximally localized on a given frequency interval, as measured by the spectral concentration.-Spectral concentration:...
). These are of great utility in disciplines such as geodesy or cosmology.
External links
- MathWorld Spheroidal Wave functions
- MathWorld Prolate Spheroidal Wave Function
- MathWorld Oblate Spheroidal Wave function