Quantum pseudo-telepathy
Encyclopedia
Quantum pseudo-telepathy is a phenomenon
in quantum game theory
resulting in anomalously high success rates in coordination game
s between separated players. These high success rates would require communication between the players in a purely classical (non-quantum) world; however, the game is set up such that during the game, communication is physically impossible. Quantum pseudo-telepathy is often and easily misrepresented as paranormal
, given that most people are not aware that the quantum laws of physics are subtly non-local
and allow violations of Bell inequalities
. This means that for quantum pseudo-telepathy to occur, prior to the game the participants need to share a physical system in an entangled quantum state
, and during the game have to execute measurements
on this entangled state as part of their game strategy. Games in which the application of such a quantum strategy leads to pseudo-telepathy are also referred to as quantum non-locality games.
In their 1999 paper, Gilles Brassard
, Richard Cleve
and Alain Tapp demonstrated that winning quantum strategies can exist in simple games for which in the absence of quantum entanglement a winning strategy can result only if the participants were allowed to communicate. The term quantum pseudo-telepathy was later introduced for this phenomenon. The prefix 'pseudo' is appropriate, as the quantum non-locality effects that are at the heart of the phenomenon do not allow any transfer of information, but rather eliminate the need to exchange information between the players for achieving a mutual win in the game.
The phenomenon of quantum pseudo-telepathy is mostly used as a powerful and explicit thought experiment
of the non-local characteristics of quantum mechanics
. Yet, the effect is real and subject to experimental verification, as demonstrated by the experimental confirmation
of the violation of the Bell inequalities.
 An example of quantum pseudo-telepathy can be observed in the following two-player coordination game in which the participants fill one row and one column of a 3x3 table with plus and minus signs.
An example of quantum pseudo-telepathy can be observed in the following two-player coordination game in which the participants fill one row and one column of a 3x3 table with plus and minus signs.
The two players Alice and Bob
are separated so that no communication between them is possible. In each round of the game Alice gets informed which row is selected, and Bob is being told which column is selected. Alice does not get to know the column Bob has been presented with, and vice versa (Bob remains unaware of the row presented to Alice). Alice and Bob both have to put the same sign in the cell common to the row and column selected. Furthermore (and this is the catch), Alice has to fill the remainder of the row such that there is an even number of signs in that row, whilst Bob has to fill the remainder of the column such that there is an odd number of signs in that column.
It is easy to see that any prior agreement between Alice and Bob on the use of specific tables filled with + and – signs is not going to help them. The reason being that such tables simply do not exist: as these would be self-contradictory with the sum of the minus signs in the table being even based on row sums, and being odd when using column sums.
So, how can Alice and Bob succeed in their task?
The trick is for Alice and Bob to share an entangled quantum state and to use specific measurements on their components of the entangled state to derive the table entries. A suitable correlated state consists of a pair of Bell state
s:
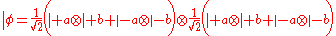
here |+> and |-> are eigenstates of the Pauli operator Sz with eigenvalues +1 and −1, respectively, whilst the subscripts a and b denote which component of each Bell state is going to Alice and which one goes to Bob.
Observables for these components can be written as products of the Pauli spin matrices
:
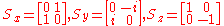
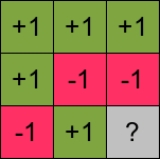
Products of these Pauli spin operators can be used to fill the 3x3 table such that each row and each column contains a mutually commuting
set of observables with eigenvalues +1 and −1, and with the product of the obervables in each row being the identity operator, and the product of observables in each column equating to minus the identity operator. This so-called Mermin
-Peres
magic square is shown in below table.
Effectively, while it is not possible to construct a 3x3 table with entries +1 and −1 such that the product of the elements in each row equals +1 and the product of elements in each column equals −1, it is possible to do so with the richer algebraic structure
based on spin matrices.
Recent studies tackle the question of the robustness of the effect against noise due to imperfect measurements on the coherent quantum state.
Phenomenon
A phenomenon , plural phenomena, is any observable occurrence. Phenomena are often, but not always, understood as 'appearances' or 'experiences'...
in quantum game theory
Quantum game theory
Quantum game theory is an extension of classical game theory to the quantum domain. It differs from classical game theory in three primary ways:#Superposed initial states,#Quantum entanglement of initial states,...
resulting in anomalously high success rates in coordination game
Coordination game
In game theory, coordination games are a class of games with multiple pure strategy Nash equilibria in which players choose the same or corresponding strategies...
s between separated players. These high success rates would require communication between the players in a purely classical (non-quantum) world; however, the game is set up such that during the game, communication is physically impossible. Quantum pseudo-telepathy is often and easily misrepresented as paranormal
Paranormal
Paranormal is a general term that designates experiences that lie outside "the range of normal experience or scientific explanation" or that indicates phenomena understood to be outside of science's current ability to explain or measure...
, given that most people are not aware that the quantum laws of physics are subtly non-local
Quantum nonlocality
Quantum nonlocality is the phenomenon by which measurements made at a microscopic level necessarily refute one or more notions that are regarded as intuitively true in classical mechanics...
and allow violations of Bell inequalities
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
. This means that for quantum pseudo-telepathy to occur, prior to the game the participants need to share a physical system in an entangled quantum state
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
, and during the game have to execute measurements
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
on this entangled state as part of their game strategy. Games in which the application of such a quantum strategy leads to pseudo-telepathy are also referred to as quantum non-locality games.
In their 1999 paper, Gilles Brassard
Gilles Brassard
Gilles Brassard was born in Montreal, Canada, in 1955. He received a Masters degree from the Université de Montréal in 1975, and obtained his Ph.D. in Computer Science from Cornell University in 1979, working in the field of cryptography with John Hopcroft as his advisor...
, Richard Cleve
Richard Cleve
Richard Erwin Cleve is a professor of computer science at the David R. Cheriton School of Computer Science at the University of Waterloo, where he holds the Institute for Quantum Computing Chair in quantum computing, and an associate member of the Perimeter Institute for Theoretical...
and Alain Tapp demonstrated that winning quantum strategies can exist in simple games for which in the absence of quantum entanglement a winning strategy can result only if the participants were allowed to communicate. The term quantum pseudo-telepathy was later introduced for this phenomenon. The prefix 'pseudo' is appropriate, as the quantum non-locality effects that are at the heart of the phenomenon do not allow any transfer of information, but rather eliminate the need to exchange information between the players for achieving a mutual win in the game.
The phenomenon of quantum pseudo-telepathy is mostly used as a powerful and explicit thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
of the non-local characteristics of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Yet, the effect is real and subject to experimental verification, as demonstrated by the experimental confirmation
Bell test experiments
The Bell test experiments serve to investigate the validity of the entanglement effect in quantum mechanics by using some kind of Bell inequality...
of the violation of the Bell inequalities.
The Mermin-Peres magic square game

The two players Alice and Bob
Alice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
are separated so that no communication between them is possible. In each round of the game Alice gets informed which row is selected, and Bob is being told which column is selected. Alice does not get to know the column Bob has been presented with, and vice versa (Bob remains unaware of the row presented to Alice). Alice and Bob both have to put the same sign in the cell common to the row and column selected. Furthermore (and this is the catch), Alice has to fill the remainder of the row such that there is an even number of signs in that row, whilst Bob has to fill the remainder of the column such that there is an odd number of signs in that column.
It is easy to see that any prior agreement between Alice and Bob on the use of specific tables filled with + and – signs is not going to help them. The reason being that such tables simply do not exist: as these would be self-contradictory with the sum of the minus signs in the table being even based on row sums, and being odd when using column sums.
So, how can Alice and Bob succeed in their task?
The trick is for Alice and Bob to share an entangled quantum state and to use specific measurements on their components of the entangled state to derive the table entries. A suitable correlated state consists of a pair of Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s:
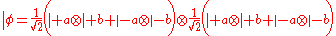
here |+> and |-> are eigenstates of the Pauli operator Sz with eigenvalues +1 and −1, respectively, whilst the subscripts a and b denote which component of each Bell state is going to Alice and which one goes to Bob.
Observables for these components can be written as products of the Pauli spin matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
:
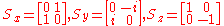
Products of these Pauli spin operators can be used to fill the 3x3 table such that each row and each column contains a mutually commuting
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
set of observables with eigenvalues +1 and −1, and with the product of the obervables in each row being the identity operator, and the product of observables in each column equating to minus the identity operator. This so-called Mermin
David Mermin
Nathaniel David Mermin is a solid-state physicist at Cornell University best known for the eponymous Mermin-Wagner theorem and his application of the term "Boojum" to superfluidity, and for the quote "Shut up and calculate!"Together with Neil W...
-Peres
Asher Peres
Asher Peres was an Israeli physicist, considered a pioneer in quantum information theory. According to his autobiography, he was born in Beaulieu-sur-Dordogne in France, where his father, a Polish electrical engineer, had found work laying down power lines...
magic square is shown in below table.
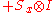 |
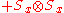 |
 |
 |
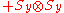 |
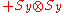 |
 |
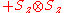 |
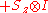 |
Effectively, while it is not possible to construct a 3x3 table with entries +1 and −1 such that the product of the elements in each row equals +1 and the product of elements in each column equals −1, it is possible to do so with the richer algebraic structure
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
based on spin matrices.
Current research
It has been demonstrated that the above described game is the simplest two-player game in which quantum pseudo-telepathy can occur. Other games in which quantum pseudo-telepathy occurs have been studied, including larger magic square games, graph colouring games giving rise to the notion of quantum chromatic number, and multiplayer games involving more than two participants.Recent studies tackle the question of the robustness of the effect against noise due to imperfect measurements on the coherent quantum state.
See also
- EPR paradoxEPR paradoxThe EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
- Kochen-Specker theoremKochen-Specker theoremIn quantum mechanics, the Kochen–Specker theorem is a "no go" theorem proved by Simon B. Kochen and Ernst Specker in 1967. It places certain constraints on the permissible types of hidden variable theories which try to explain the apparent randomness of quantum mechanics as a deterministic model...
- Quantum information scienceQuantum information scienceQuantum information science is an area of study based on the idea that information science depends on quantum effects in physics. It includes theoretical issues in computational models as well as more experimental topics in quantum physics including what can and cannot be done with quantum...
- QubitQubitIn quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
- Tsirelson's boundTsirelson's boundTsirelson's bound, also known as Tsirelson's inequality, or in another transliteration, Cirel'son's inequality, is an inequality that imposed an upper limit to quantum mechanical correlations between distant events...
- Wheeler-Feynman absorber theory

