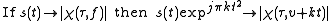Radar ambiguity function
Encyclopedia
In pulsed radar
and sonar
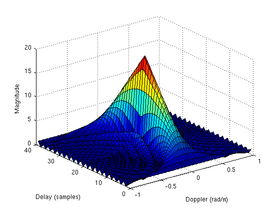
signal processing, an ambiguity function is a two-dimensional function of time delay and Doppler frequency
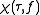 showing the distortion
showing the distortion
of a returned pulse due to the receiver matched filter
(commonly, but not exclusively, used in pulse compression
radar) due to the Doppler shift of the return from a moving target. The ambiguity
function is determined by the properties of the pulse
and the matched filter
, and not any particular target scenario. Many definitions of the ambiguity function exist; Some are restricted to narrowband signals and others are suitable to describe the propagation delay
and Doppler relationship of wideband signals. Often the definition of the ambiguity function is given as the magnitude squared of other definitions (Weiss).
For a given complex
baseband
pulse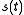 , the narrowband ambiguity function is given by
, the narrowband ambiguity function is given by
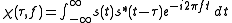
where denotes the complex conjugate
denotes the complex conjugate
and is the imaginary unit
is the imaginary unit
. Note that for zero Doppler shift ( ) this reduces to the autocorrelation
) this reduces to the autocorrelation
of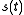 . A more concise way of representing the
. A more concise way of representing the
ambiguity function consists of examining the one-dimensional
zero-delay and zero-Doppler "cuts"; that is,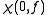 and
and
 , respectively. The matched filter output as a function of a time (the signal one would observe in a radar system) is a delay cut, with constant frequency given by the target's Doppler shift:
, respectively. The matched filter output as a function of a time (the signal one would observe in a radar system) is a delay cut, with constant frequency given by the target's Doppler shift: 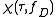 .
.
. This relationship is fundamental to the formulation of other time–frequency distributions which are obtained by a 2-dimensional filtering in the ambiguity domain (that is, the ambiguity function of the signal), leading to the definition of a class of TFDs that are better adapted to the signals considered.
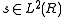 is :
is :
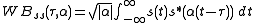
where is a time scale factor of the received signal relative to the transmitted signal given by:
is a time scale factor of the received signal relative to the transmitted signal given by:

for a target moving with constant radial velocity v. The reflection of the signal is represented with compression (or expansion) in time by the factor , which is equivalent to a compression by the factor
, which is equivalent to a compression by the factor 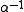 in the frequency domain (with an amplitude scaling). When the wave speed in the medium is sufficiently faster than the target speed, as is common with RADAR, this compression in frequency is closely approximated by a shift in frequency Δf = fc*v/c (known as the doppler shift). This approximation results in the narrowband ambiguity function given above, which can be computed efficiently by making use of the FFT algorithm.
in the frequency domain (with an amplitude scaling). When the wave speed in the medium is sufficiently faster than the target speed, as is common with RADAR, this compression in frequency is closely approximated by a shift in frequency Δf = fc*v/c (known as the doppler shift). This approximation results in the narrowband ambiguity function given above, which can be computed efficiently by making use of the FFT algorithm.
or
"thumbtack" function; that is, a function which is infinite at (0,0) and
zero elsewhere.

An ambiguity function of this kind would be somewhat of a misnomer; it
would have no ambiguities at all, and both the zero-delay and zero-Doppler cuts would be an impulse
. However, any Doppler shift would make the target disappear. This is not desirable if a target has unknown velocity it will disappear from the radar picture, but if Doppler
processing is independently performed, knowledge of the precise
Doppler frequency allows ranging without interference
from any other targets which are not also moving at exactly the same
velocity.
This type of ambiguity function is not physically realizable; that is, there is no pulse that will produce
that will produce  from the definition of the ambiguity function. Approximations exist, however, and binary phase-shift keyed waveforms using maximal-length sequences are the best known performers in this regard
from the definition of the ambiguity function. Approximations exist, however, and binary phase-shift keyed waveforms using maximal-length sequences are the best known performers in this regard
.
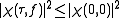
(2) Symmetry about the origin
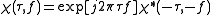
(3) Volume invariance
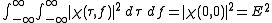
(4) Modulation
(5) Frequency energy spectrum
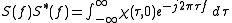
 Consider a simple square pulse of duration
Consider a simple square pulse of duration  and
and
amplitude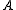 :
:
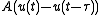
where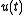 is the Heaviside step function
is the Heaviside step function
. The
matched filter output is given by the autocorrelation
of the pulse, which is a triangular pulse of height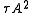 and
and
duration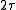 (the zero-Doppler cut). However, if the
(the zero-Doppler cut). However, if the
measured pulse has a frequency offset due to Doppler shift, the
matched filter output is distorted into a sinc function. The
greater the Doppler shift, the smaller the peak of the resulting sinc,
and the more difficult it is to detect the target.
In general, the square pulse is not a desirable waveform from a pulse compression standpoint, because the autocorrelation function is too short in amplitude, making it difficult to detect targets in noise, and too wide in time, making it difficult to discern multiple overlapping targets.
 A commonly used radar
A commonly used radar
or sonar
pulse is the linear frequency modulated (LFM) pulse (or "chirp"). It has the advantage of greater bandwidth while keeping the pulse duration short and envelope constant. A constant envelope LFM pulse has an ambiguity function similar to that of the square pulse, except that it is skewed in the delay-Doppler plane. Slight Doppler mismatches for the LFM pulse do not change the general shape of the pulse and reduce the amplitude very little, but they do appear to shift the pulse
in time. Thus, an uncompensated Doppler shift changes the target's apparent range; this phenomenon is called range-Doppler coupling.
as a special case).
For these types of radar, the simple linear relationship between time and range that exists in the monostatic case no longer applies, and is instead dependent on the specific geometry – i.e. the relative location of transmitter(s), receiver(s) and target. Therefore the multistatic ambiguity function is mostly usefully defined as a function of two- or three-dimensional position and velocity vectors for a given multistatic geometry and transmitted waveform.
Just as the monostatic ambiguity function is naturally derived from the matched filter, the multistatic ambiguity function is derived from the corresponding optimal multistatic detector – i.e. that which maximizes the probability of detection given a fixed probability of false alarm through joint processing of the signals at all receivers. The nature of this detection algorithm depends on whether or not the target fluctuations observed by each bistatic pair within the multistatic system are mutually correlated. If so, the optimal detector performs phase coherent summation of received signals which can result in very high target location accuracy. If not, the optimal detector performs incoherent summation of received signals which gives diversity gain. Such systems are sometimes described as MIMO radars due to the information theoretic similarities to MIMO
communication systems.
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
and sonar
Sonar
Sonar is a technique that uses sound propagation to navigate, communicate with or detect other vessels...
signal processing, an ambiguity function is a two-dimensional function of time delay and Doppler frequency
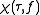 showing the distortion
showing the distortionDistortion
A distortion is the alteration of the original shape of an object, image, sound, waveform or other form of information or representation. Distortion is usually unwanted, and often many methods are employed to minimize it in practice...
of a returned pulse due to the receiver matched filter
Matched filter
In telecommunications, a matched filter is obtained by correlating a known signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template...
(commonly, but not exclusively, used in pulse compression
Pulse compression
Pulse compression is a signal processing technique mainly used in radar, sonar and echography to increase the range resolution as well as the signal to noise ratio...
radar) due to the Doppler shift of the return from a moving target. The ambiguity
function is determined by the properties of the pulse
Pulse (signal processing)
In signal processing, the term pulse has the following meanings:#A rapid, transient change in the amplitude of a signal from a baseline value to a higher or lower value, followed by a rapid return to the baseline value....
and the matched filter
Matched filter
In telecommunications, a matched filter is obtained by correlating a known signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template...
, and not any particular target scenario. Many definitions of the ambiguity function exist; Some are restricted to narrowband signals and others are suitable to describe the propagation delay
Propagation delay
Propagation delay is a technical term that can have a different meaning depending on the context. It can relate to networking, electronics or physics...
and Doppler relationship of wideband signals. Often the definition of the ambiguity function is given as the magnitude squared of other definitions (Weiss).
For a given complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
baseband
Baseband
In telecommunications and signal processing, baseband is an adjective that describes signals and systems whose range of frequencies is measured from close to 0 hertz to a cut-off frequency, a maximum bandwidth or highest signal frequency; it is sometimes used as a noun for a band of frequencies...
pulse
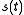 , the narrowband ambiguity function is given by
, the narrowband ambiguity function is given by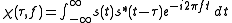
where
 denotes the complex conjugate
denotes the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
and
 is the imaginary unit
is the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. Note that for zero Doppler shift (
 ) this reduces to the autocorrelation
) this reduces to the autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of
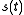 . A more concise way of representing the
. A more concise way of representing theambiguity function consists of examining the one-dimensional
zero-delay and zero-Doppler "cuts"; that is,
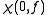 and
and , respectively. The matched filter output as a function of a time (the signal one would observe in a radar system) is a delay cut, with constant frequency given by the target's Doppler shift:
, respectively. The matched filter output as a function of a time (the signal one would observe in a radar system) is a delay cut, with constant frequency given by the target's Doppler shift: 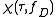 .
.Relationship to time–frequency distributions
The ambiguity function plays a key role in the field of time–frequency signal processing, as it is related to the Wigner–Ville distribution by a 2 Dimensional Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. This relationship is fundamental to the formulation of other time–frequency distributions which are obtained by a 2-dimensional filtering in the ambiguity domain (that is, the ambiguity function of the signal), leading to the definition of a class of TFDs that are better adapted to the signals considered.
Wideband ambiguity function
The wideband ambiguity function of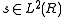 is :
is :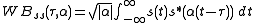
where
 is a time scale factor of the received signal relative to the transmitted signal given by:
is a time scale factor of the received signal relative to the transmitted signal given by:
for a target moving with constant radial velocity v. The reflection of the signal is represented with compression (or expansion) in time by the factor
 , which is equivalent to a compression by the factor
, which is equivalent to a compression by the factor 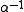 in the frequency domain (with an amplitude scaling). When the wave speed in the medium is sufficiently faster than the target speed, as is common with RADAR, this compression in frequency is closely approximated by a shift in frequency Δf = fc*v/c (known as the doppler shift). This approximation results in the narrowband ambiguity function given above, which can be computed efficiently by making use of the FFT algorithm.
in the frequency domain (with an amplitude scaling). When the wave speed in the medium is sufficiently faster than the target speed, as is common with RADAR, this compression in frequency is closely approximated by a shift in frequency Δf = fc*v/c (known as the doppler shift). This approximation results in the narrowband ambiguity function given above, which can be computed efficiently by making use of the FFT algorithm.Ideal ambiguity function
An ambiguity function of interest is a 2-dimensional Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
or
"thumbtack" function; that is, a function which is infinite at (0,0) and
zero elsewhere.

An ambiguity function of this kind would be somewhat of a misnomer; it
would have no ambiguities at all, and both the zero-delay and zero-Doppler cuts would be an impulse
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. However, any Doppler shift would make the target disappear. This is not desirable if a target has unknown velocity it will disappear from the radar picture, but if Doppler
processing is independently performed, knowledge of the precise
Doppler frequency allows ranging without interference
from any other targets which are not also moving at exactly the same
velocity.
This type of ambiguity function is not physically realizable; that is, there is no pulse
 that will produce
that will produce 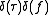 from the definition of the ambiguity function. Approximations exist, however, and binary phase-shift keyed waveforms using maximal-length sequences are the best known performers in this regard
from the definition of the ambiguity function. Approximations exist, however, and binary phase-shift keyed waveforms using maximal-length sequences are the best known performers in this regard.
Properties of the ambiguity function
(1) Maximum value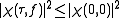
(2) Symmetry about the origin
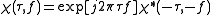
(3) Volume invariance
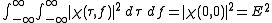
(4) Modulation
(5) Frequency energy spectrum
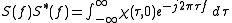
Square pulse

 and
andamplitude
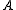 :
: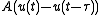
where
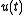 is the Heaviside step function
is the Heaviside step functionHeaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
. The
matched filter output is given by the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of the pulse, which is a triangular pulse of height
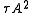 and
andduration
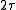 (the zero-Doppler cut). However, if the
(the zero-Doppler cut). However, if themeasured pulse has a frequency offset due to Doppler shift, the
matched filter output is distorted into a sinc function. The
greater the Doppler shift, the smaller the peak of the resulting sinc,
and the more difficult it is to detect the target.
In general, the square pulse is not a desirable waveform from a pulse compression standpoint, because the autocorrelation function is too short in amplitude, making it difficult to detect targets in noise, and too wide in time, making it difficult to discern multiple overlapping targets.
LFM pulse

Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
or sonar
Sonar
Sonar is a technique that uses sound propagation to navigate, communicate with or detect other vessels...
pulse is the linear frequency modulated (LFM) pulse (or "chirp"). It has the advantage of greater bandwidth while keeping the pulse duration short and envelope constant. A constant envelope LFM pulse has an ambiguity function similar to that of the square pulse, except that it is skewed in the delay-Doppler plane. Slight Doppler mismatches for the LFM pulse do not change the general shape of the pulse and reduce the amplitude very little, but they do appear to shift the pulse
in time. Thus, an uncompensated Doppler shift changes the target's apparent range; this phenomenon is called range-Doppler coupling.
Multistatic ambiguity functions
The ambiguity function can be extended to multistatic radars, which comprise multiple non-colocated transmitters and/or receivers (and can include bistatic radarBistatic radar
Bistatic radar is the name given to a radar system which comprises a transmitter and receiver which are separated by a distance that is comparable to the expected target distance. Conversely, a radar in which the transmitter and receiver are collocated is called a monostatic radar...
as a special case).
For these types of radar, the simple linear relationship between time and range that exists in the monostatic case no longer applies, and is instead dependent on the specific geometry – i.e. the relative location of transmitter(s), receiver(s) and target. Therefore the multistatic ambiguity function is mostly usefully defined as a function of two- or three-dimensional position and velocity vectors for a given multistatic geometry and transmitted waveform.
Just as the monostatic ambiguity function is naturally derived from the matched filter, the multistatic ambiguity function is derived from the corresponding optimal multistatic detector – i.e. that which maximizes the probability of detection given a fixed probability of false alarm through joint processing of the signals at all receivers. The nature of this detection algorithm depends on whether or not the target fluctuations observed by each bistatic pair within the multistatic system are mutually correlated. If so, the optimal detector performs phase coherent summation of received signals which can result in very high target location accuracy. If not, the optimal detector performs incoherent summation of received signals which gives diversity gain. Such systems are sometimes described as MIMO radars due to the information theoretic similarities to MIMO
MIMO
In radio, multiple-input and multiple-output, or MIMO , is the use of multiple antennas at both the transmitter and receiver to improve communication performance. It is one of several forms of smart antenna technology...
communication systems.
Further reading
- Richards, Mark A. Fundamentals of Radar Signal Processing. McGraw–Hill Inc., 2005. ISBN 0-07-144474-2.
- Ipatov, Valery P. Spread Spectrum and CDMA. Wiley & Sons, 2005. ISBN 0-470-09178-9
- Chernyak V.S. Fundamentals of Multisite Radar Systems, CRC Press, 1998.
See also
- Matched filterMatched filterIn telecommunications, a matched filter is obtained by correlating a known signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template...
- Pulse compressionPulse compressionPulse compression is a signal processing technique mainly used in radar, sonar and echography to increase the range resolution as well as the signal to noise ratio...
- Pulse-Doppler radarPulse-doppler radarPulse-Doppler is a 4D radar system capable of detecting both target 3D location as well as measuring radial velocity . It uses the Doppler effect to avoid overloading computers and operators as well as to reduce power consumption...
- Digital signal processingDigital signal processingDigital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...