Singly even number
Encyclopedia
In mathematics
an even integer
, that is, a number that is divisible by 2, is called evenly even or doubly even if it is a multiple of 4, and oddly even or singly even if it is not. (The former names are traditional ones, derived from the ancient Greek; the latter have become common in recent decades.)
These names reflect a basic concept in number theory
, the 2-order of an integer: how many times the integer can be divided by 2. This is equivalent to the multiplicity
of 2 in the prime factorization.
A singly even number can be divided by 2 only once; it is even but its quotient by 2 is odd.
A doubly even number is an integer that is divisible more than once by 2; it is even and its quotient by 2 is also even.
The separate consideration of oddly and evenly even numbers is useful in many parts of mathematics, especially in number theory, combinatorics
, coding theory
(see even code
s), among others.
and later writers such as Nicomachus
. Today, there is a standard development of the concepts. The 2-order or 2-adic order is simply a special case of the p-adic order at a general prime number
p; see p-adic number
for more on this broad area of mathematics. Many of the following definitions generalize directly to other primes.
For an integer n, the 2-order of n (also called valuation) is the largest natural number ν such that 2ν divides n. This definition applies to positive and negative numbers n, although some authors restrict it to positive n; and one may define the 2-order of 0 to be infinity (see also parity of zero). The 2-order of n is written ν2(n) or ord2(n). It is not to be confused with the multiplicative order
modulo 2
.
The 2-order provides a unified description of various classes of integers defined by evenness:
One can also extend the 2-order to the rational numbers by defining ν2(q) to be the unique integer ν where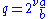
and a and b are both odd. For example, half-integer
s have a negative 2-order, namely −1. Finally, by defining the 2-adic norm,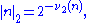
one is well on the way to constructing the 2-adic numbers.
is to reach a score of 0, so the player with the smaller score is in a better position to win. At the beginning of a leg, "smaller" has the usual meaning of absolute value
, and the basic strategy is to aim at high-value areas on the dartboard and score as many points as possible. At the end of a leg, since one needs to double out to win, the 2-adic norm becomes the relevant measure. With any odd score no matter how small in absolute value, it takes at least two darts to win. Any even score between 2 and 40 can be satisfied with a single dart, and 40 is a much more desirable score than 2, due to the effects of missing.
A common miss when aiming at the double ring is to hit a single instead and accidentally halve one's score. Given a score of 22 — a singly even number — one has a game shot for double 11. If one hits single 11, the new score is 11, which is odd, and it will take at least two further darts to recover. By contrast, when shooting for double 12, one may make the same mistake but still have 3 game shots in a row: D12, D6, and D3. Generally, with a score of , one has such game shots. This is why is such a desirable score: it splits 5 times.
is irrational
operates by infinite descent
. Usually, the descent part of the proof is abstracted away by assuming (or proving) the existence of irreducible
representations of rational number
s. An alternate approach is to exploit the existence of the ν2 operator.
Assume by contradiction that
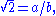
where a and b do not have to be in lowest terms. Then applying ν2 to the equation yields
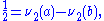
which is absurd. Therefore √2 is irrational.
More concretely, since the valuation of 2b2 is odd, while valuation of a2 is even, they must be distinct integers, so that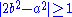
. An easy calculation then yields a lower bound of 
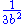for the difference 
, yielding a direct proof of irrationality not relying on the law of excluded middle.
, many properties of manifolds depend only on their dimension mod 4 or mod 8; thus one often studies manifolds of singly even and doubly even dimension (4k+2 and 4k) as classes. For example, doubly even dimensional manifolds have a symmetric nondegenerate bilinear form on their middle-dimension cohomology group, which thus has an integer-valued signature
. Conversely, singly even dimensional manifolds have a skew-symmetric
nondegenerate bilinear form on their middle dimension; if one defines a quadratic refinement of this to a quadratic form
(as on a framed manifold), one obtains the Arf invariant
as a mod 2 invariant. Odd dimensional manifolds, by contrast, do not have these invariants, though in algebraic surgery theory one may define more complicated invariants. This 4-fold and 8-fold periodicity in the structure of manifolds is related to the 4-fold periodicity of L-theory
and the 8-fold periodicity of real topological K-theory
, which is known as Bott periodicity – note further that real K-theory is 4-fold periodic away from 2.
If a compact
oriented smooth spin manifold has dimension , or exactly, then its signature
is an integer multiple of 16.
. It cannot be represented as a difference of two squares
. However, a singly even number can be represented as the difference of two pronic number
s or of two powerful numbers.
In group theory
, it is relatively simple to show that the order of a nonabelian
finite simple group cannot be a singly even number. In fact, by the Feit–Thompson theorem
, it cannot be odd either, so every such group has doubly even order.
Lambert's continued fraction for the tangent function gives the following continued fraction
involving the positive singly even numbers:
This expression leads to similar representations of e
.
In organic chemistry
, Hückel's rule
, also known as the 4n + 2 rule, predicts that a cyclic
π-bond
system containing a simply even number of p electron
s will be aromatic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
an even integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, that is, a number that is divisible by 2, is called evenly even or doubly even if it is a multiple of 4, and oddly even or singly even if it is not. (The former names are traditional ones, derived from the ancient Greek; the latter have become common in recent decades.)
These names reflect a basic concept in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the 2-order of an integer: how many times the integer can be divided by 2. This is equivalent to the multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of 2 in the prime factorization.
A singly even number can be divided by 2 only once; it is even but its quotient by 2 is odd.
A doubly even number is an integer that is divisible more than once by 2; it is even and its quotient by 2 is also even.
The separate consideration of oddly and evenly even numbers is useful in many parts of mathematics, especially in number theory, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
(see even code
Even code
A binary code is called an even code if the Hamming weight of all its codewords is even. An even code should have a generator polynomial that include minimal polynomial as a product. Furthermore, a binary code is called doubly even if the Hamming weight of all its codewords is divisible by 4...
s), among others.
Definitions
The ancient Greek terms "even-times-even" and "even-times-odd" were given various inequivalent definitions by EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
and later writers such as Nicomachus
Nicomachus
Nicomachus was an important mathematician in the ancient world and is best known for his works Introduction to Arithmetic and Manual of Harmonics in Greek. He was born in Gerasa, in the Roman province of Syria , and was strongly influenced by Aristotle...
. Today, there is a standard development of the concepts. The 2-order or 2-adic order is simply a special case of the p-adic order at a general prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p; see p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
for more on this broad area of mathematics. Many of the following definitions generalize directly to other primes.
For an integer n, the 2-order of n (also called valuation) is the largest natural number ν such that 2ν divides n. This definition applies to positive and negative numbers n, although some authors restrict it to positive n; and one may define the 2-order of 0 to be infinity (see also parity of zero). The 2-order of n is written ν2(n) or ord2(n). It is not to be confused with the multiplicative order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
modulo 2
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
.
The 2-order provides a unified description of various classes of integers defined by evenness:
- Odd numbers are those with ν2(n) = 0, i.e., integers of the form .
- Even numbers are those with ν2(n) > 0, i.e., integers of the form . In particular:
- Singly even numbers are those with ν2(n) = 1, i.e., integers of the form .
- Doubly even numbers are those with ν2(n) > 1, i.e., integers of the form .
- In this terminology, a doubly even number may or may not be divisible by 8, so there is no particular terminology for "triply even" numbers.
One can also extend the 2-order to the rational numbers by defining ν2(q) to be the unique integer ν where
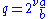
and a and b are both odd. For example, half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
s have a negative 2-order, namely −1. Finally, by defining the 2-adic norm,
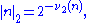
one is well on the way to constructing the 2-adic numbers.
Safer outs in darts
The object of the game of dartsDarts
Darts is a form of throwing game where darts are thrown at a circular target fixed to a wall. Though various boards and games have been used in the past, the term "darts" usually now refers to a standardised game involving a specific board design and set of rules...
is to reach a score of 0, so the player with the smaller score is in a better position to win. At the beginning of a leg, "smaller" has the usual meaning of absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
, and the basic strategy is to aim at high-value areas on the dartboard and score as many points as possible. At the end of a leg, since one needs to double out to win, the 2-adic norm becomes the relevant measure. With any odd score no matter how small in absolute value, it takes at least two darts to win. Any even score between 2 and 40 can be satisfied with a single dart, and 40 is a much more desirable score than 2, due to the effects of missing.
A common miss when aiming at the double ring is to hit a single instead and accidentally halve one's score. Given a score of 22 — a singly even number — one has a game shot for double 11. If one hits single 11, the new score is 11, which is odd, and it will take at least two further darts to recover. By contrast, when shooting for double 12, one may make the same mistake but still have 3 game shots in a row: D12, D6, and D3. Generally, with a score of , one has such game shots. This is why is such a desirable score: it splits 5 times.
Irrationality of √2
The classic proof that the square root of 2Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
operates by infinite descent
Infinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
. Usually, the descent part of the proof is abstracted away by assuming (or proving) the existence of irreducible
Irreducible fraction
An irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
representations of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. An alternate approach is to exploit the existence of the ν2 operator.
Assume by contradiction that
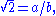
where a and b do not have to be in lowest terms. Then applying ν2 to the equation yields
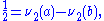
which is absurd. Therefore √2 is irrational.
More concretely, since the valuation of 2b2 is odd, while valuation of a2 is even, they must be distinct integers, so that
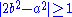. An easy calculation then yields a lower bound of 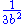for the difference , yielding a direct proof of irrationality not relying on the law of excluded middle.Geometric topology
In geometric topologyGeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, many properties of manifolds depend only on their dimension mod 4 or mod 8; thus one often studies manifolds of singly even and doubly even dimension (4k+2 and 4k) as classes. For example, doubly even dimensional manifolds have a symmetric nondegenerate bilinear form on their middle-dimension cohomology group, which thus has an integer-valued signature
Signature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
. Conversely, singly even dimensional manifolds have a skew-symmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
nondegenerate bilinear form on their middle dimension; if one defines a quadratic refinement of this to a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
(as on a framed manifold), one obtains the Arf invariant
Arf invariant
In mathematics, the Arf invariant of a nonsingular quadratic form over a field of characteristic 2 was defined by when he started the systematic study of quadratic forms over arbitrary fields of characteristic2. The Arf invariant is the substitute, in...
as a mod 2 invariant. Odd dimensional manifolds, by contrast, do not have these invariants, though in algebraic surgery theory one may define more complicated invariants. This 4-fold and 8-fold periodicity in the structure of manifolds is related to the 4-fold periodicity of L-theory
L-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
and the 8-fold periodicity of real topological K-theory
Topological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
, which is known as Bott periodicity – note further that real K-theory is 4-fold periodic away from 2.
If a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
oriented smooth spin manifold has dimension , or exactly, then its signature
Signature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
is an integer multiple of 16.
Other appearances
A singly even number cannot be a powerful numberPowerful number
A powerful number is a positive integer m such that for every prime number p dividing m, p2 also divides m. Equivalently, a powerful number is the product of a square and a cube, that is, a number m of the form m = a2b3, where a and b are positive integers. Powerful numbers are also known as...
. It cannot be represented as a difference of two squares
Difference of two squares
In mathematics, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number...
. However, a singly even number can be represented as the difference of two pronic number
Pronic number
A pronic number, oblong number, rectangular number or heteromecic number, is a number which is the product of two consecutive integers, that is, n . The n-th pronic number is twice the n-th triangular number and n more than the n-th square number...
s or of two powerful numbers.
In group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, it is relatively simple to show that the order of a nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
finite simple group cannot be a singly even number. In fact, by the Feit–Thompson theorem
Feit–Thompson theorem
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by - History : conjectured that every nonabelian finite simple group has even order...
, it cannot be odd either, so every such group has doubly even order.
Lambert's continued fraction for the tangent function gives the following continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
involving the positive singly even numbers:
This expression leads to similar representations of e
Representations of e
The mathematical constant e can be represented in a variety of ways as a real number. Since e is an irrational number , it cannot be represented as a fraction, but it can be represented as a continued fraction...
.
In organic chemistry
Organic chemistry
Organic chemistry is a subdiscipline within chemistry involving the scientific study of the structure, properties, composition, reactions, and preparation of carbon-based compounds, hydrocarbons, and their derivatives...
, Hückel's rule
Hückel's rule
In organic chemistry, Hückel's rule estimates whether a planar ring molecule will have aromatic properties. The quantum mechanical basis for its formulation was first worked out by physical chemist Erich Hückel in 1931...
, also known as the 4n + 2 rule, predicts that a cyclic
Cyclic compound
In chemistry, a cyclic compound is a compound in which a series of atoms is connected to form a loop or ring.While the vast majority of cyclic compounds are organic, a few inorganic substances form cyclic compounds as well, including sulfur, silanes, phosphanes, phosphoric acid, and triboric acid. ...
π-bond
Pi bond
In chemistry, pi bonds are covalent chemical bonds where two lobes of one involved atomic orbital overlap two lobes of the other involved atomic orbital...
system containing a simply even number of p electron
Electron configuration
In atomic physics and quantum chemistry, electron configuration is the arrangement of electrons of an atom, a molecule, or other physical structure...
s will be aromatic.
Related classifications
Although the 2-order can detect when an integer is congruent to 0 (mod 4) or 2 (mod 4), it cannot tell the difference between 1 (mod 4) or 3 (mod 4). This distinction has some interesting consequences, such as Fermat's theorem on sums of two squares.External links
- singly even number at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...