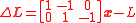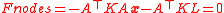Spring system
Encyclopedia
In engineering and physics, a spring system or spring network is a model of physics described as a graph
with a position at each vertex and a spring
of given stiffness and length along each edge. This generalizes Hooke's law
to higher dimensions. This simple model can be used to solve the pose of static systems from crystal lattice to springs. A spring system can be thought of as the simplest case of the finite element method
for solving problems in statics
. Assuming linear springs and small deformation (or restricting to one-dimensional motion) a spring system can be cast as a (possibly overdetermined) system of linear equations or equivalently as an energy minimization
problem.
Consider the simple case of three nodes connected by two springs. Then the stretching of the two springs is given as a function of the positions of the nodes by
Let A be that "connectivity matrix", relating each degree of freedom to the direction each spring pulls on it.
So the forces on the springs is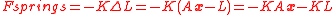
where K is a diagonal matrix
giving the stiffnesses of all of the springs. Then the force on the nodes is given by left multiplying by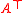 , which we set to zero to find equilibrium:
, which we set to zero to find equilibrium:
which gives the linear equation:
Now,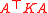 is singular, because all solutions are equivalent up to rigid-body translation. Let us prescribe a Dirichlet boundary condition
is singular, because all solutions are equivalent up to rigid-body translation. Let us prescribe a Dirichlet boundary condition
, e.g.,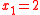 .
.
Suppose K is the identity and so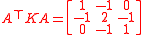 .
.
If we plug in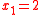 we have
we have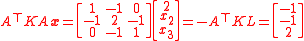 .
.
Incorporating the 2 to the left-hand side gives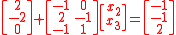 .
.
and removing rows of the system that we already know, and simplifying, leaves us with .
.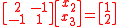 .
.
so we can then solve .
.
That is,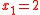 , as prescribed, and
, as prescribed, and 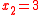 , leaving the first spring slack, and
, leaving the first spring slack, and  , leaving the second spring slack.
, leaving the second spring slack.
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with a position at each vertex and a spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
of given stiffness and length along each edge. This generalizes Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
to higher dimensions. This simple model can be used to solve the pose of static systems from crystal lattice to springs. A spring system can be thought of as the simplest case of the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
for solving problems in statics
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
. Assuming linear springs and small deformation (or restricting to one-dimensional motion) a spring system can be cast as a (possibly overdetermined) system of linear equations or equivalently as an energy minimization
Energy minimization
In computational chemistry, energy minimization methods are used to compute the equilibrium configuration of molecules and solids....
problem.
Known spring lengths
If the nominal lengths, L, of the springs are known to be 1 and 2 units respectively, then the system can be solved as followed:Consider the simple case of three nodes connected by two springs. Then the stretching of the two springs is given as a function of the positions of the nodes by
Let A be that "connectivity matrix", relating each degree of freedom to the direction each spring pulls on it.
So the forces on the springs is
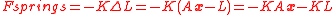
where K is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
giving the stiffnesses of all of the springs. Then the force on the nodes is given by left multiplying by
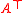 , which we set to zero to find equilibrium:
, which we set to zero to find equilibrium:
which gives the linear equation:
-
 .
.
Now,
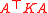 is singular, because all solutions are equivalent up to rigid-body translation. Let us prescribe a Dirichlet boundary condition
is singular, because all solutions are equivalent up to rigid-body translation. Let us prescribe a Dirichlet boundary conditionDirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
, e.g.,
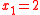 .
.Suppose K is the identity and so
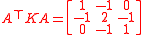 .
.If we plug in
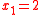 we have
we have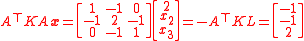 .
.Incorporating the 2 to the left-hand side gives
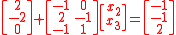 .
.and removing rows of the system that we already know, and simplifying, leaves us with
 .
.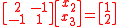 .
.so we can then solve
 .
.That is,
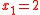 , as prescribed, and
, as prescribed, and 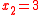 , leaving the first spring slack, and
, leaving the first spring slack, and  , leaving the second spring slack.
, leaving the second spring slack.See also
- Gaussian network modelGaussian network modelThe Gaussian network model is a representation of a biological macromolecule as an elastic mass-and-spring network to study, understand, and characterize mechanical aspects of its long-scale dynamics...
- Anisotropic Network ModelAnisotropic Network ModelThe Anisotropic Network Model is a simple yet powerful tool made for Normal Mode Analysis of proteins, which has been successfully applied for exploring the relation between function and dynamics for many proteins...
- Stiffness matrix
- Spring-mass system
- Laplacian matrixLaplacian matrixIn the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...