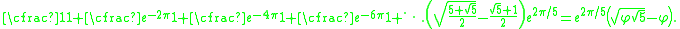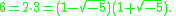
Square root of 5
Encyclopedia
| Binary Binary numeral system The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2... |
10.0011110001101111... |
| Decimal Decimal The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations.... |
2.23606797749978969... |
| Hexadecimal Hexadecimal In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen... |
2.3C6EF372FE94F82C... |
| Continued fraction Continued fraction In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on... |
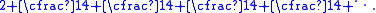 |
The square root of 5 is the positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
that, when multiplied by itself, gives the prime number 5. It is more precisely called the principal square root of 5, to distinguish it from the negative number with the same property. This number appears in the fractional expression for the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. It can be denoted in surd
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
form as:
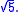
It is an irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
. The first sixty significant digits of its decimal expansion are:
- 2.23606 79774 99789 69640 91736 68731 27623 54406 18359 61152 57242 7089...
which can be rounded down to 2.236 to within 99.99% accuracy. As of April 1994, its numerical value in decimal had been computed to at least one million digits.
Proof of irrationality
Suppose that √5 is rational, and express it in lowest possible terms (i.e., as a fully reduced fraction) as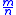 for natural numbers m and n. Then √5 can be expressed in lower terms as
for natural numbers m and n. Then √5 can be expressed in lower terms as 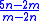 , which is a contradiction.
, which is a contradiction.Continued fraction
It can be expressed as the continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
[2; 4, 4, 4, 4, 4...] . The sequence of best rational approximations is:
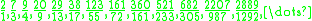
Convergent
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
s of the continued fraction are colored; their numerators are 2, 9, 38, 161, ... , and their denominators are 1, 4, 17, 72, ... . The other (non-colored) terms are semiconvergents.
Babylonian method
When is computed with the Babylonian method, starting with r0 = 2 and using rn+1 = (rn + 5/rn) / 2, the nth approximant rn is equal to the 2n-th convergent of the convergent sequence:
is computed with the Babylonian method, starting with r0 = 2 and using rn+1 = (rn + 5/rn) / 2, the nth approximant rn is equal to the 2n-th convergent of the convergent sequence: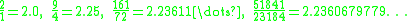
Relation to the golden ratio and Fibonacci numbers
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ is the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of 1 and the square root of 5. The algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic relationship between the square root of 5, the golden ratio and the conjugate of the golden ratio (
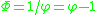 ) are expressed in the following formulae:
) are expressed in the following formulae: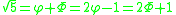
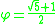
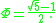
(See section below for their geometrical interpretation as decompositions of a root-5 rectangle.)
The square root of 5 then naturally figures in the closed form expression for the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s, a formula which is usually written in terms of the golden ratio:
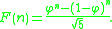
The quotient of √5 and φ (or the product of √5 and Φ), and its reciprocal, provide an interesting pattern of continued fractions and are related to the ratios between the Fibonacci numbers and the Lucas number
Lucas number
The Lucas numbers are an integer sequence named after the mathematician François Édouard Anatole Lucas , who studied both that sequence and the closely related Fibonacci numbers...
s:
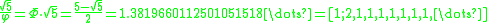
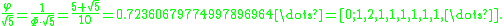
The series of convergents to these values feature the series of Fibonacci numbers and the series of Lucas number
Lucas number
The Lucas numbers are an integer sequence named after the mathematician François Édouard Anatole Lucas , who studied both that sequence and the closely related Fibonacci numbers...
s as numerators and denominators, and viceversa, respectively:
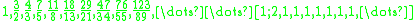
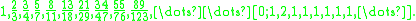
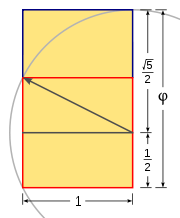
Geometry
GeometricallyGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the square root of 5 corresponds to the diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
of a rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
whose sides are of length 1 and 2, as is evident from the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. Such a rectangle can be obtained by halving a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, or by placing two equal squares side by side. Together with the algebraic relationship between √5 and φ, this forms the basis for the geometrical construction of a golden rectangle from a square, and for the construction of a regular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
given its side (since the side-to-diagonal ratio in a regular pentagon is φ).
Forming a dihedral
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
with the two equal squares that halve a 1:2 rectangle, it can be seen that √5 corresponds also to the ratio between the length of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
and the shortest distance from one of its vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
to the opposite one, when traversing the cube surface (the shortest distance when traversing through the inside of the cube corresponds to the length of the cube diagonal, which is the square root of three times the edge).
The number √5 can be algebraically and geometrically related to the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
and the square root of 3
Square root of 3
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is more precisely called the principal square root of 3, to distinguish it from the negative number with the same property...
, as it is the length of the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
of a right triangle with catheti
Cathetus
In a right triangle, the cathetus , commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called the periphrasis . The side opposite the right angle is the hypotenuse...
measuring √2 and √3 (again, the Pythagorean theorem proves this). Right triangles of such proportions can be found inside a cube: the sides of any triangle defined by the centre
Centre (geometry)
In geometry, the centre of an object is a point in some sense in the middle of the object. If geometry is regarded as the study of isometry groups then the centre is a fixed point of the isometries.-Circles:...
point of a cube, one of its vertices, and the middle point of a side located on one the faces containing that vertex and opposite to it, are in the ratio √2:√3:√5. This follows from the geometrical relationships between a cube and the quantities √2 (edge-to-face-diagonal ratio, or distance between opposite edges), √3 (edge-to-cube-diagonal ratio) and √5 (the relationship just mentioned above).
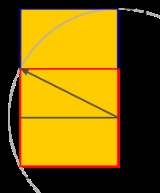
A rectangle with side proportions 1:√5 is called a root-five rectangle and is part of the series of root rectangles, a subset of dynamic rectangle
Dynamic rectangle
A dynamic rectangle is a right-angled, four-sided figure with dynamic symmetry, which in this case, means that aspect ratio is a distinguished value in dynamic symmetry, a proportioning system and natural design methodology described in Jay Hambidge's books...
s, which are based on √1 (= 1), √2, √3, √4 (= 2), √5... and successively constructed using the diagonal of the previous root rectangle, starting from a square. A root-5 rectangle is particularly notable in that it can be split into a square and two equal golden rectangles (of dimensions Φ × 1), or into two golden rectangles of different sizes (of dimensions Φ × 1 and 1 × φ). It can also be decomposed as the union of two equal golden rectangles (of dimensions 1 × φ) whose intersection forms a square. All this is can be seen as the geometric interpretation of the algebraic relationships between √5, φ and Φ mentioned above. The root-5 rectangle can be constructed from a 1:2 rectangle (the root-4 rectangle), or directly from a square in a manner similar to the one for the golden rectangle shown in the illustration, but extending the arc of length to both sides.
Trigonometry
Like √2 and √3, the square root of five appears extensively in the formulae for exact trigonometric constantsExact trigonometric constants
Exact constant expressions for trigonometric values are sometimes useful, mainly for simplifying solutions into radical forms which allow further simplification....
, and as such the computation of its value is important for generating trigonometric tables
Generating trigonometric tables
In mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering...
. Since √5 is geometrically linked to half-square rectangles and to pentagons, it also appears frequently in formulae for the geometric properties of figures derived from them, such as in the formula for the volume of a dodecahedron.
Diophantine approximations
Hurwitz's theoremHurwitz's theorem (number theory)
In number theory, Hurwitz's theorem, named after Adolf Hurwitz, gives a bound on a Diophantine approximation. The theorem states that for every irrational number ξ there are infinitely many rationals m/n such that...
in Diophantine approximations states that every irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
x can be approximated by infinitely many rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s m/n in lowest terms in such a way that
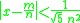
and that √5 is best possible, in the sense that for any larger constant than √5, there are some irrational numbers x for which only finitely many such approximations exist.
Closely related to this is the theorem that of any three consecutive convergent
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
s
pi/qi,
pi+1/qi+1,
pi+2/qi+2,
of a number α, at least one of the three inequalities holds:
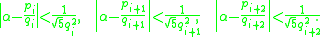
And the √5 in the denominator is the best bound possible since the convergents of the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
make the difference on the left-hand side arbitrarily close to the value on the right-hand side. In particular, one cannot obtain a tighter bound by considering sequences of four or more consecutive convergents.
Algebra
The ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
 contains numbers of the form
contains numbers of the form 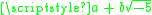 , where a and b are integer
, where a and b are integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and
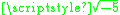 is the imaginary number
is the imaginary numberImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
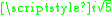 . This ring is a frequently cited example of an integral domain that is not a unique factorization domain
. This ring is a frequently cited example of an integral domain that is not a unique factorization domainUnique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
. The number 6 has two inequivalent factorizations within this ring:
The field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
 , like any other quadratic field
, like any other quadratic fieldQuadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
, is an abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
of the rational numbers. The Kronecker–Weber theorem
Kronecker–Weber theorem
In algebraic number theory, the Kronecker–Weber theorem states that every finite abelian extension of the field of rational numbers Q, or in other words, every algebraic number field whose Galois group over Q is abelian, is a subfield of a cyclotomic field, i.e. a field obtained by adjoining a root...
therefore guarantees that the square root of five can be written as a rational linear combination of roots of unity:
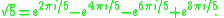
Identities of Ramanujan
The square root of 5 appears in various identities of RamanujanSrinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
involving continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s.
For example, this case of the Rogers–Ramanujan continued fraction
Rogers–Ramanujan continued fraction
The Rogers–Ramanujan continued fraction is a continued fraction discovered by and later studied by Srinivasa Ramanujan, closely related to the Rogers-Ramanujan identities, that can be evaluated explicitly for special values of its argument....
: