Superselection
Encyclopedia
In Quantum mechanics
, superselection extends the concept of selection rules.
Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence
between eigenstates of certain observables.
It was originally introduced by Wick, Wightman, and Wigner to impose additional restrictions to quantum theory beyond those of selection rules.
Mathematically speaking, two quantum states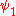
and 
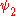are separated by a selection rule if 
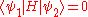for any given Hamiltonian 
, while they are separated by a superselection rule if 
for all physical observables 
.
A superselection sector is a concept used in quantum mechanics
when a representation
of a *-algebra
is decomposed into irreducible components. It formalizes the idea that not all self-adjoint operator
s are observable
s because the relative phase of a superposition of nonzero states from different irreducible components is not observable (the expectation values of the observables can't distinguish between them).
whose self-adjoint
elements correspond to observables. A unitary representation
of O may be decomposed as the direct sum of irreducible unitary representations of O. Each isotypic component
in this decomposition is called a superselection sector. Observables preserve the superselection sectors.
in the sense that for all g in G, a in A and ψ in H,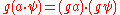
Suppose that O is an invariant
subalgebra of A under G (all observables are invariant under G, but not every self-adjoint operator invariant under G is necessarily an observable). H decomposes into superselection sectors, each of which is the tensor product of in irreducible representation of G with a representation of O.
This can be generalized by assuming that H is only a representation of an extension or cover K of G. (For instance G could be the Lorentz group, and K the corresponding spin double cover.) Alternatively, one can replace G by a Lie algebra
, Lie superalgebra
or a Hopf algebra
.
A big system often has superselection sectors. In a solid, different rotations and translations which are not lattice symmetries define superselection sectors. In general, a superselection rule is a quantity that can never change through local fluctuations. Aside from order parameters like the magnetization of a magnet, there are also topological quantities, like the winding number. If a string is wound around a circular wire, the total number of times it winds around never changes under local fluctuations. This is an ordinary conservation law. If the wire is an infinite line, under conditions that the vacuum does not have winding number fluctuations which are coherent throughout the system, the conservation law is a superselection rule --- the probability that the winding will unwind is zero.
There are quantum fluctuations, superpositions arising from different configurations of a phase-type path integral, and statistical fluctuations from a Boltzmann type path integral. Both of these path integrals have the property that large changes in an effectively infinite system require an improbable conspiracy between the fluctuations. So there are both statistical mechanical and quantum mechanical superselection rules.
In a theory where the vacuum is invariant under a symmetry, the conserved charge leads to superselection sectors in the case that the charge is conserved. Electric charge is conserved in our universe, so it seems at first like a trivial example. But when a superconductor fills space, or equivalently in a Higgs phase, electric charge is still globally conserved but no longer defines the superselection sectors. The sloshing of the superconductor can bring charges into any volume at very little cost. In this case, the superselection sectors of the vacuum are labeled by the direction of the Higgs field. Since different Higgs directions are related by an exact symmetry, they are all exactly equivalent. This suggests a deep relationship between symmetry breaking directions and conserved charges.
, at low temperature
s, there are two distinct pure states, one with the average spin pointing up and the other with the average spin pointing down. This is the ordered phase. At high temperatures, there is only one pure state with an average spin of zero. This is the disordered phase. At the phase transition
between the two, the symmetry between spin up and spin down is broken.
Below the phase transition temperature, an infinite ising model can be in either the mostly-plus or the mostly-minus configuration. If it starts in the mostly-plus phase, it will never reach the mostly-minus, even though flipping all the spins will give the same energy. By changing the temperature, the system acquired a new superselection rule--- the average spin. There are two superselection sectors--- mostly minus and mostly plus.
There are also other superselection sectors; for instance, states where the left half of the plane is mostly plus and the right half of the plane is mostly minus.
When a new superselection rule appears, the system has spontaneously ordered. Above the critical temperature, the ising model is disordered. It could visit every state in principle. Below the transition, the system chooses one of two possibilities at random and never changes its mind.
For any finite system, the superselection is imperfect. An Ising model on a finite lattice will eventually fluctuate from the mostly plus to the mostly minus at any nonzero temperature, but it takes a very long time. The amount of time is exponentially small in the size of the system measured in correlation lengths, so for all practical purposes the flip never happens even in systems only a few times larger than the correlation length.
, and the energy or action only depends on combinations which are symmetric under rotations of these components into each other, the contributions with the lowest dimension are (summation convention):
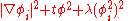
and define the action in a quantum field context or free energy in the statistical context. There are two phases. When t is large, the potential tends to move the average
to zero. For t large and negative, the quadratic potential pushes 
out, but the quartic potential prevents it from becoming infinite. If this is done in a quantum path integral, this is a quantum phase transition, in a classical partition function, a classical phase transition.
So as t moves toward more negative values in either context, the field has to choose some direction to point. Once it does this, it cannot change its mind. The system has ordered. In the ordered phase, there is still a little bit of symmetry--- rotations around the axis of the breaking. The field can point in any direction labelled by all the points on a unit sphere in
space, which is the coset
space of the unbroken SO(2) subgroup in the full symmetry group SO(3).
In the disordered phase, the superselection sectors are described by the representation of SO(3) under which a given configuration transforms globally. Because the SO(3) is unbroken, different representations will not mix with each other. No local fluctuation will ever bring in nontrivial SO(3) configurations from infinity. A local configuration is entirely defined by its representation.
There is a mass gap, or a correlation length, which separates configurations with a nontrivial SO(3) transformations from the rotationally invariant vacuum. This is true until the critical point in t where the mass gap disappears and the correlation length is infinite. The vanishing gap is a sign that the fluctuations in the SO(3) field are about to condense.
In the ordered region, there are field configurations which can carry topological charge. These are labeled by elements of the second homotopy group
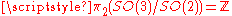. Each of these describe a different field configuration which at large distances from the origin is a winding configuration. Although each such isolated configuration has infinite energy, it labels superselection sectors where the difference in energy between two states is finite. In addition, pairs of winding configurations with opposite topological charge can be produced copiously as the transition is approached from below.
When the winding number is zero, so that the field everywhere points in the same direction, there is an additional infinity of superselection sectors, each labelled by a different value of the unbroken SO(2) charge.
In the ordered state, there is a mass gap for the superselection sectors labeled by a nonzero integer, because the topological solitons are massive even infinitely massive. But there is no mass gap
for the all the superselection sectors labeled by zero because there are massless Goldstone boson
s describing fluctuations in the direction of the condensate.
If the field values are identified under a Z2 reflection (corresponding to flipping the sign of all the
fields), the superselection sectors are labelled by a nonnegative integer (the absolute value of the topological charge).
It is interesting that O(3) charges only make sense in the disordered phase and not at all in the ordered phase. This is because when the symmetry is broken there is a condensate
which is charged, which is not invariant under the symmetry group. Conversely, the topological charge only makes sense in the ordered phase and not at all in the disordered phase, because in some hand-waving way there is a "topological condensate" in the disordered phase which randomizes the field from point to point. The randomizing can be thought of as crossing many condensed topological winding boundaries.
The very question of what charges are meaningful depends very much on the phase. Approaching the phase transition from the disordered side, the mass of the charges particles approaches zero. Approaching it from the ordered side, the mass gap associated with fluctuations of the topological solitions approaches zero.
In the standard model
of particle physics, in the electroweak sector,
the low energy model is SU(2) and U(1) broken to U(1) by a Higgs doublet. The
only superselection rule determining the configuration is the total electric charge.
If there are monopoles, then the monopole charge must be included.
If the Higgs t parameter is varied so that it does not acquire a vacuum expectation
value, the universe is now symmetric under an unbroken SU(2) and U(1) gauge group. If
the SU(2) has infinitesimally weak couplings, so that it only confines at enormous
distances, then the representation of the SU(2) group and the U(1) charge both are
superselection rules. But if the SU(2) has a nonzero coupling then the superselection
sectors are separated by infinite mass because the mass of any state in a nontrivial representation is infinite.
By changing the temperature, the Higgs fluctuations can zero out the expectation value at
a finite temperature. Above this temperature, the SU(2) and U(1) quantum numbers describe
the superselection sectors. Below the phase transition, only electric charge defines the superselection sector.
Chiral Quark Condensate
Consider the global flavour
symmetry of QCD
in the chiral limit where the masses of the quark
s are zero. This is not exactly the universe in which we live, where the up and down quarks have a tiny but nonzero mass, but it is a very good approximation, to the extent that isospin is conserved.
Below a certain temperature which is the symmetry restoration temperature, the phase is ordered.
The chiral condensate forms, and pions of small mass are produced. The SU(Nf) charges, Isospin
and Hypercharge
and SU(3), make sense. Above the QCD temperature lies a disordered phase where SU(Nf)×SU(Nf) and color SU(3) charges make sense.
It is an open question whether the deconfinement temperature of QCD is also the temperature at which the chiral condensate melts.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, superselection extends the concept of selection rules.
Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence
Coherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
between eigenstates of certain observables.
It was originally introduced by Wick, Wightman, and Wigner to impose additional restrictions to quantum theory beyond those of selection rules.
Mathematically speaking, two quantum states
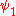and 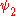are separated by a selection rule if 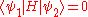for any given Hamiltonian , while they are separated by a superselection rule if for all physical observables .A superselection sector is a concept used in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
when a representation
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of a *-algebra
Star-algebra
-*-ring:In mathematics, a *-ring is an associative ring with a map * : A → A which is an antiautomorphism and an involution.More precisely, * is required to satisfy the following properties:* ^* = x^* + y^** ^* = y^* x^** 1^* = 1...
is decomposed into irreducible components. It formalizes the idea that not all self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s are observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s because the relative phase of a superposition of nonzero states from different irreducible components is not observable (the expectation values of the observables can't distinguish between them).
Formulation
Suppose A is a unital *-algebra and O is a unital *-subalgebraSubalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
whose self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
elements correspond to observables. A unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of O may be decomposed as the direct sum of irreducible unitary representations of O. Each isotypic component
Isotypic component
The Isotypic component of weight \lambda of a Lie algebra module is the sum of all submodules which are isomorphic to the highest weight module with weight \lambda.-Definition:...
in this decomposition is called a superselection sector. Observables preserve the superselection sectors.
Relationship to symmetry
Symmetries often give rise to superselection sectors (although this is not the only way they occur). Suppose a group G acts upon A, and that H is a unitary representation of both A and G which is equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
in the sense that for all g in G, a in A and ψ in H,
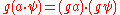
Suppose that O is an invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
subalgebra of A under G (all observables are invariant under G, but not every self-adjoint operator invariant under G is necessarily an observable). H decomposes into superselection sectors, each of which is the tensor product of in irreducible representation of G with a representation of O.
This can be generalized by assuming that H is only a representation of an extension or cover K of G. (For instance G could be the Lorentz group, and K the corresponding spin double cover.) Alternatively, one can replace G by a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
or a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
.
Examples
Consider a quantum mechanical particle confined to a closed loop (i.e., a periodic line of period L). The superselection sectors are labeled by an angle θ between 0 and 2π. All the wave functions within a single superselection sector satisfySuperselection Sectors
A large physical system with infinitely many degrees of freedom does not always visit every possible state, even if it has enough energy. If a magnet is magnetized in a certain direction, each spin will fluctuate at any temperature, but the net magnetization will never change. The reason is that it is infinitely improbable that all the infinitely many spins at each different position will all fluctuate together in the same way.A big system often has superselection sectors. In a solid, different rotations and translations which are not lattice symmetries define superselection sectors. In general, a superselection rule is a quantity that can never change through local fluctuations. Aside from order parameters like the magnetization of a magnet, there are also topological quantities, like the winding number. If a string is wound around a circular wire, the total number of times it winds around never changes under local fluctuations. This is an ordinary conservation law. If the wire is an infinite line, under conditions that the vacuum does not have winding number fluctuations which are coherent throughout the system, the conservation law is a superselection rule --- the probability that the winding will unwind is zero.
There are quantum fluctuations, superpositions arising from different configurations of a phase-type path integral, and statistical fluctuations from a Boltzmann type path integral. Both of these path integrals have the property that large changes in an effectively infinite system require an improbable conspiracy between the fluctuations. So there are both statistical mechanical and quantum mechanical superselection rules.
In a theory where the vacuum is invariant under a symmetry, the conserved charge leads to superselection sectors in the case that the charge is conserved. Electric charge is conserved in our universe, so it seems at first like a trivial example. But when a superconductor fills space, or equivalently in a Higgs phase, electric charge is still globally conserved but no longer defines the superselection sectors. The sloshing of the superconductor can bring charges into any volume at very little cost. In this case, the superselection sectors of the vacuum are labeled by the direction of the Higgs field. Since different Higgs directions are related by an exact symmetry, they are all exactly equivalent. This suggests a deep relationship between symmetry breaking directions and conserved charges.
Discrete Symmetry
In the 2D Ising modelIsing model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, at low temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
s, there are two distinct pure states, one with the average spin pointing up and the other with the average spin pointing down. This is the ordered phase. At high temperatures, there is only one pure state with an average spin of zero. This is the disordered phase. At the phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
between the two, the symmetry between spin up and spin down is broken.
Below the phase transition temperature, an infinite ising model can be in either the mostly-plus or the mostly-minus configuration. If it starts in the mostly-plus phase, it will never reach the mostly-minus, even though flipping all the spins will give the same energy. By changing the temperature, the system acquired a new superselection rule--- the average spin. There are two superselection sectors--- mostly minus and mostly plus.
There are also other superselection sectors; for instance, states where the left half of the plane is mostly plus and the right half of the plane is mostly minus.
When a new superselection rule appears, the system has spontaneously ordered. Above the critical temperature, the ising model is disordered. It could visit every state in principle. Below the transition, the system chooses one of two possibilities at random and never changes its mind.
For any finite system, the superselection is imperfect. An Ising model on a finite lattice will eventually fluctuate from the mostly plus to the mostly minus at any nonzero temperature, but it takes a very long time. The amount of time is exponentially small in the size of the system measured in correlation lengths, so for all practical purposes the flip never happens even in systems only a few times larger than the correlation length.
Continuous Symmetries
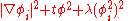
If a statistical or quantum field has three real valued scalar fields, and the energy or action only depends on combinations which are symmetric under rotations of these components into each other, the contributions with the lowest dimension are (summation convention):and define the action in a quantum field context or free energy in the statistical context. There are two phases. When t is large, the potential tends to move the average
to zero. For t large and negative, the quadratic potential pushes out, but the quartic potential prevents it from becoming infinite. If this is done in a quantum path integral, this is a quantum phase transition, in a classical partition function, a classical phase transition.So as t moves toward more negative values in either context, the field has to choose some direction to point. Once it does this, it cannot change its mind. The system has ordered. In the ordered phase, there is still a little bit of symmetry--- rotations around the axis of the breaking. The field can point in any direction labelled by all the points on a unit sphere in
space, which is the cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
space of the unbroken SO(2) subgroup in the full symmetry group SO(3).
In the disordered phase, the superselection sectors are described by the representation of SO(3) under which a given configuration transforms globally. Because the SO(3) is unbroken, different representations will not mix with each other. No local fluctuation will ever bring in nontrivial SO(3) configurations from infinity. A local configuration is entirely defined by its representation.
There is a mass gap, or a correlation length, which separates configurations with a nontrivial SO(3) transformations from the rotationally invariant vacuum. This is true until the critical point in t where the mass gap disappears and the correlation length is infinite. The vanishing gap is a sign that the fluctuations in the SO(3) field are about to condense.
In the ordered region, there are field configurations which can carry topological charge. These are labeled by elements of the second homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
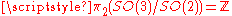. Each of these describe a different field configuration which at large distances from the origin is a winding configuration. Although each such isolated configuration has infinite energy, it labels superselection sectors where the difference in energy between two states is finite. In addition, pairs of winding configurations with opposite topological charge can be produced copiously as the transition is approached from below.When the winding number is zero, so that the field everywhere points in the same direction, there is an additional infinity of superselection sectors, each labelled by a different value of the unbroken SO(2) charge.
In the ordered state, there is a mass gap for the superselection sectors labeled by a nonzero integer, because the topological solitons are massive even infinitely massive. But there is no mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
for the all the superselection sectors labeled by zero because there are massless Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
s describing fluctuations in the direction of the condensate.
If the field values are identified under a Z2 reflection (corresponding to flipping the sign of all the
fields), the superselection sectors are labelled by a nonnegative integer (the absolute value of the topological charge).It is interesting that O(3) charges only make sense in the disordered phase and not at all in the ordered phase. This is because when the symmetry is broken there is a condensate
Condensate
Condensate may refer to:* The liquid phase produced by the condensation of steam or any other gas* The product of a chemical condensation reaction, other than water* Natural gas condensate, in the natural gas industry- Quantum physics :...
which is charged, which is not invariant under the symmetry group. Conversely, the topological charge only makes sense in the ordered phase and not at all in the disordered phase, because in some hand-waving way there is a "topological condensate" in the disordered phase which randomizes the field from point to point. The randomizing can be thought of as crossing many condensed topological winding boundaries.
The very question of what charges are meaningful depends very much on the phase. Approaching the phase transition from the disordered side, the mass of the charges particles approaches zero. Approaching it from the ordered side, the mass gap associated with fluctuations of the topological solitions approaches zero.
Examples in Particle Physics
Higgs MechanismIn the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics, in the electroweak sector,
the low energy model is SU(2) and U(1) broken to U(1) by a Higgs doublet. The
only superselection rule determining the configuration is the total electric charge.
If there are monopoles, then the monopole charge must be included.
If the Higgs t parameter is varied so that it does not acquire a vacuum expectation
value, the universe is now symmetric under an unbroken SU(2) and U(1) gauge group. If
the SU(2) has infinitesimally weak couplings, so that it only confines at enormous
distances, then the representation of the SU(2) group and the U(1) charge both are
superselection rules. But if the SU(2) has a nonzero coupling then the superselection
sectors are separated by infinite mass because the mass of any state in a nontrivial representation is infinite.
By changing the temperature, the Higgs fluctuations can zero out the expectation value at
a finite temperature. Above this temperature, the SU(2) and U(1) quantum numbers describe
the superselection sectors. Below the phase transition, only electric charge defines the superselection sector.
Chiral Quark Condensate
Consider the global flavour
Flavour (particle physics)
In particle physics, flavour or flavor is a quantum number of elementary particles. In quantum chromodynamics, flavour is a global symmetry...
symmetry of QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
in the chiral limit where the masses of the quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s are zero. This is not exactly the universe in which we live, where the up and down quarks have a tiny but nonzero mass, but it is a very good approximation, to the extent that isospin is conserved.
Below a certain temperature which is the symmetry restoration temperature, the phase is ordered.
The chiral condensate forms, and pions of small mass are produced. The SU(Nf) charges, Isospin
Isospin
In physics, and specifically, particle physics, isospin is a quantum number related to the strong interaction. This term was derived from isotopic spin, but the term is confusing as two isotopes of a nucleus have different numbers of nucleons; in contrast, rotations of isospin maintain the number...
and Hypercharge
Hypercharge
In particle physics, the hypercharge Y of a particle is related to the strong interaction, and is distinct from the similarly named weak hypercharge, which has an analogous role in the electroweak interaction...
and SU(3), make sense. Above the QCD temperature lies a disordered phase where SU(Nf)×SU(Nf) and color SU(3) charges make sense.
It is an open question whether the deconfinement temperature of QCD is also the temperature at which the chiral condensate melts.